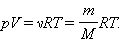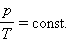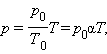МОЛЬ - единица количества вещества

ОПРЕДЕЛЕНИЕ

Моль — это такое количество вещества, которое содержит число молекул (частиц, ионов, атомов), равное числу Авогадро NA=6⋅1023.

Число 6,02⋅1023 называют числом Авогадро в честь итальянского химика Амедео Авогадро. Почему именно это число выбрано для определения моль? Дело в том, что ровно столько атомов содержится в 12 г изотопа углерода 12C. В 8-м классе вы узнали, что этот же изотоп используют для выбора атомной единицы массы.

Число Авогадро называют также постоянной Авогадро и обозначают NA. Эта постоянная имеет размерность — штук на моль, или, если штуки не упоминать, моль–1. Таким образом,

NA = 6,02⋅1023 моль–1.

Для приближенных расчетов число Авогадро можно округлять до 6⋅1023.

Зная постоянную Авогадро, мы можем любое количество вещества выразить в моль. Если вещество содержит N молекул (или структурных единиц), то количество вещества (обозначается греческой буквой ν) равно:

ν = NNA.

Размерность количества вещества: [ν] = 1/моль−1 = моль.

Наоборот, зная количество вещества в моль, можно найти число молекул:

N =ν⋅NA.

32.

Закон Авога́дро — закон, согласно которому в равных объёмах различных газов, взятых при одинаковых температурах и давлениях, содержится одно и то же количество молекул. В виде гипотезы был сформулирован в 1811 году Амедео Авогадро (1776—1856), профессором физики в Турине. Гипотеза была подтверждена многочисленными экспериментальными исследованиями и поэтому стала называться законом Авогадро, став впоследствии (через 50 лет, после съезда химиков в Карлсруэ) количественной основой современной химии (стехиометрии)

Следствия закона[править | править код]

Первое следствие из закона Авогадро: один моль (одинаковое количество молей) любого газа при одинаковых — изобаричных и изотермичных — условиях занимает одинаковый объём.

Согласно закону Авогадро, одно и то же количество молекул любого газа занимает при одинаковых условиях один и тот же объём. С другой стороны, 1 моль любого вещества содержит (по определению) одинаковое количество частиц (англ.)русск. (например, молекул). Отсюда следует, что при определённых температуре и давлении 1 моль любого вещества в газообразном состоянии занимает один и тот же объём.

В частности, при нормальных условиях, то есть при 0 °C (273 К) и 101,3 кПа, объём 1 моля газа равен 22,413(962) л (л/моль). Этот объём называют молярным объёмом газа V_m. Пересчитать эту величину на другие температуру и давление можно с помощью уравнения Клапейрона:

{\displaystyle {\frac {PV}{T}}={\frac {101,3~kPa\cdot 22,414~l}{273~K}}} .

Второе следствие из закона Авогадро: молярная масса первого газа равна произведению молярной массы второго газа на относительную плотность первого газа ко второму.

Положение это имело громадное значение для развития химии (химии идеального газа^{[прим 1]}), так как оно дает возможность определять частичный вес^{[прим 2]} тел, способных переходить в газообразное или парообразное состояние (см. Атомно-молекулярное учение). Если через m мы обозначим частичный вес тела, и через d — удельный вес^{[прим 3]} его в парообразном состоянии, то отношение m / d должно быть постоянным для всех тел. Опыт показал, что для всех изученных тел, переходящих в пар без разложения, эта постоянная равна 28,9, если при определении частичного веса исходить из удельного веса воздуха, принимаемого за единицу; но эта постоянная будет равняться 2, если принять за единицу удельный вес водорода. Обозначив эту постоянную, или, что то же, общий всем парам и газам частичный объём через С, мы из формулы имеем с другой стороны m = dC. Так как удельный вес пара определяется легко, то, подставляя значение d в формулу, выводится и неизвестный частичный вес данного тела.

Элементарный анализ, например, одного из полибутиленов указывает, в нём пайное отношение углерода к водороду, как 1 к 2, а потому частичный вес его может быть выражен формулой СН₂ или C₂H₄, C₄H₈ и вообще (СН₂)_n. Частичный вес этого углеводорода тотчас определяется, следуя закону Авогадро, раз мы знаем удельный вес, то есть плотность его пара; он определён Бутлеровым и оказался 5,85 (по отношению к воздуху); то есть частичный вес его будет 5,85 · 28,9 = 169,06. Формуле C₁₁H₂₂ отвечает частичный вес 154, формуле C₁₂H₂₄ — 168, а C₁₃H₂₆ — 182. Формула C₁₂H₂₄ близко отвечает наблюдаемой величине, а потому она и должна выражать собою величину частицы нашего углеводорода (CH₂)_n.

33.

ОПРЕДЕЛЕНИЕ

Моль — это такое количество вещества, которое содержит число молекул (частиц, ионов, атомов), равное числу Авогадро NA=6⋅1023.

Число 6,02⋅1023 называют числом Авогадро в честь итальянского химика Амедео Авогадро. Почему именно это число выбрано для определения моль? Дело в том, что ровно столько атомов содержится в 12 г изотопа углерода 12C. В 8-м классе вы узнали, что этот же изотоп используют для выбора атомной единицы массы.

Число Авогадро называют также постоянной Авогадро и обозначают NA. Эта постоянная имеет размерность — штук на моль, или, если штуки не упоминать, моль–1. Таким образом,

NA = 6,02⋅1023 моль–1.

Для приближенных расчетов число Авогадро можно округлять до 6⋅1023.

Зная постоянную Авогадро, мы можем любое количество вещества выразить в моль. Если вещество содержит N молекул (или структурных единиц), то количество вещества (обозначается греческой буквой ν) равно:

ν = NNA.

Размерность количества вещества: [ν] = 1/моль−1 = моль.

Наоборот, зная количество вещества в моль, можно найти число молекул:

N =ν⋅NA.

Количество вещества в химии измеряется в моль и обозначается n. Ранее было принято обозначение ν, поэтому в данный момент в литературе можно встретить оба обозначения.

Например, 1 моль меди содержит NA=6⋅1023 атомов,

1 моль поваренной соли — NA=6⋅1023 молекул NaCl.

1 моль ионов натрия — NA=6⋅1023 ионов Na+.

34.

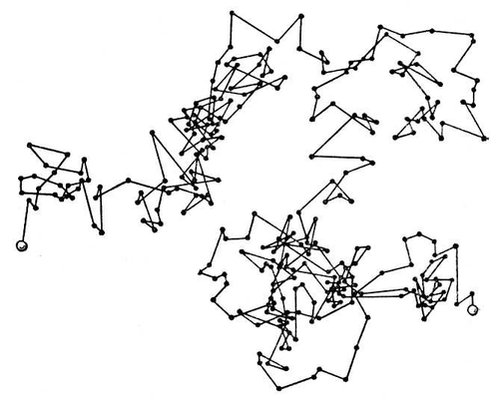
Молекулы находятся в непрерывном хаотическом движении. С ростом температуры скорость частиц вещества увеличивается, поэтому хаотическое движение частиц принято называть тепловым. Экспериментальным подтверждением непрерывного движения атомов и молекул в веществе является броуновское движение и диффузия.

ОПРЕДЕЛЕНИЕ

Броуновское движение — тепловое движение мельчайших частиц, взвешенных в жидкости или газе.

ОПРЕДЕЛЕНИЕ

Диффузия — проникновение молекул одного вещества в промежутки между молекулами другого. Чем выше температура, тем быстрее происходит диффузия.

35.

Вещества могут находиться в различных агрегатных состояниях: твердом, жидком, газообразном. Молекулярные силы в разных агрегатных состояниях различны: в твердом состоянии они наибольшие, в газообразном — наименьшие. Различием молекулярных сил объясняются свойства, которые проявляются в разных агрегатных состояниях:

· твердые тела сохраняют объем и форму (несжимаемы), имеют кристаллическое строение, характеризуются плотной упаковкой и дальним порядком в расположении частиц;

· жидкости текучи, практически не сжимаются (сохраняют объем), принимают форму сосуда, характеризуются плотной упаковкой и ближним порядком в расположении частиц;

· газы легко сжимаются, полностью занимают весь предоставленный им объем, имеют малую плотность, характеризуются большими расстояниями и слабым взаимодействием частиц вещества.

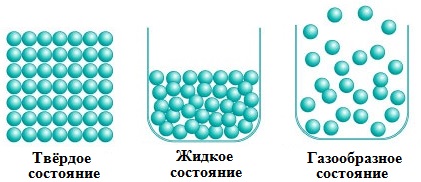
В твердых телах расстояние между молекулами маленькое и преобладают силы взаимодействия. Поэтому твердые тела обладают свойством сохранять форму и объем. Молекулы твердых тел находятся в постоянном движении, но каждая молекула движется около положения равновесия.

В жидкостях расстояние между молекулами побольше, значит, меньше и силы взаимодействия. Поэтому жидкость сохраняет объем, но легко меняет форму.

В газах силы взаимодействия совсем невелики, так как расстояние между молекулами газа в несколько десятков раз больше размеров молекул. Поэтому газ занимает весь предоставленный ему объем.

36.

Энергия, которой обладает тело благодаря своей температуре, называется тепловой. При передаче телу энергии для увеличения его тепловой энергии частицы тела:

• получают кинетическую энергию с повышением температуры;

• используют получаемую энергию для разрыва связей между молекулами, если тело переходит из твердого состояния в жидкое или газообразное либо из жидкого в газообразное.

Удельной теплоемкостью материала называется количество энергии, необходимое для повышения температуры единицы его массы на один градус. Чтобы повысить температуру тела массой m с Т₁ на Т₂, нужно передать ему энергию Е = mc(T₂ — Т₁), где с — удельная теплоемкость материала. Единицей теплоемкости с служит Дж/кг К или Дж/моль К.

Удельной теплотой фазового перехода твердого или жидкого тела называется количество энергии, необходимое для того, чтобы единица массы материала перешла из одного состояния в другое без изменения температуры. Для изменения состояния тела массой m при постоянной температуре нужно передать ему энергию ΔЕ = mI, где I — удельная фазовая теплота плавления, испарения или сублимации (перехода непосредственно из твердого в газообразное состояние, минуя стадию жидкости) данного материала. Единицей I служит Дж/кг или Дж/моль.

Тепловым расширением называется процесс изменения размеров твердого тела при нагревании. При повышении температуры твердого или жидкого тела его частицы совершают колебания с большей средней амплитудой, что и служит причиной расширения объема тела. Увеличение размеров пропорционально начальным размерам и изменению температуры. Коэффициентом линейного расширения материала α называется отношение увеличения линейных размеров к единицам длины и температуры. Единицей α служит К-1. Если тело длиной L нагревать от температуры Т₁ до температуры Т₂, то увеличение длины составит Δ L = αL (Т₂ — Т₁).

37.

	Кельвин	Градус Цельсия	Градус Фаренгейта
Абсолютный ноль	0 K	−273,15 °C	−459,67 °F
Температура кипения жидкого азота	77,4 K	−195,8 °C	−320,3 °F
Сублимация (переход из твёрдого состояния в газообразное) сухого льда	195,1 K	−78 °C	−108,4 °F
Точка пересечения шкал Цельсия и Фаренгейта	233,15 K	−40 °C	−40 °F
Температура плавления льда	273,1499 K	−0,0001 °C	31,99982 °F
Тройная точка воды	273,16 K	0,01 °C	32,018 °F
Нормальная температура человеческого тела	310 K	37,0 °C	98,6 °F
Температура кипения воды при давлении в 1 атмосферу (101,325 кПа)	373,1339 K	99,9839 °C	211,971 °F

Градус Цельсия - применяется в Международной системе единиц (СИ) наряду с кельвином.

Градус Цельсия назван в честь шведского учёного Андерса Цельсия, предложившего в 1742 году новую шкалу для измерения температуры.

Первоначальное определение градуса Цельсия зависело от определения стандартного атмосферного давления, потому что и температура кипения воды и температура таяния льда зависят от давления. Это не очень удобно для стандартизации единицы измерения. Поэтому после принятия кельвина K, в качестве основной единицы измерения температуры, определение градуса Цельсия было пересмотрено.

Градус Фаренгейта.

Назван в честь немецкого учёного Габриеля Фаренгейта, предложившего в 1724 году шкалу для измерения температуры.

На шкале Фаренгейта точка таяния льда равна +32 °F, а точка кипения воды +212 °F (при нормальном атмосферном давлении). При этом один градус Фаренгейта равен 1/180 разности этих температур. Диапазон 0…+100 °F по шкале Фаренгейта примерно соответствует диапазону −18…+38 °C по шкале Цельсия. Ноль на этой шкале определяется по температуре замерзания смеси воды, соли и нашатыря (1:1:1), а за 96 °F принята нормальная температура человеческого тела.

Кельвин (до 1968 года градус Кельвина) - единица термодинамической температуры в Международной системе единиц (СИ), одна из семи основных единиц СИ. Предложена в 1848 году. 1 кельвин равен 1/273,16 части термодинамической температуры тройной точки воды. Начало шкалы (0 К) совпадает с абсолютным нулём.

Пересчёт в градусы Цельсия: °С = K−273,15 (температура тройной точки воды — 0,01 °C).

Единица названа в честь английского физика Уильяма Томсона, которому было пожаловано звание лорд Кельвин Ларгский из Айршира. В свою очередь, это звание пошло от реки Кельвин (River Kelvin), протекающей через территорию университета в Глазго.

38.

Упрощенный вывод основного уравнения МКТ[

Пусть имеется {\displaystyleN}N частиц массой {\displaystylem_{0}}M0 в некотором кубическом сосуде.

Так как молекулы движутся хаотически, то события, состоящие в движении в одном из шести независимых направлений пространства, совпадающих с осями декартовой системы координат, равновероятны.

Поэтому, в каждом из этих направлении движется {\displaystyle {\frac {1}{6}}N} 1/6N частиц.

Пусть все частицы обладают одинаковой скоростью {\displaystylev}

V

.

Каждая из частиц, сталкивающихся со стенкой, передаёт ей импульс {\displaystyle \DeltaP=2m_{0}v}deltaP=2M0V.

Если площадь стенки {\displaystyleS}S, а концентрация - {\displaystylen}N, то количество частиц, сталкивающихся со стенкой за время {\displaystyle \Deltat}deltaT равно N=1/6nsdeltatv{\displaystyleN={\frac {1}{6}}nS\Deltatv} .

Так как {\displaystylep={\frac {F}{S}}}p=F/s, а {\displaystyleF={\frac {\DeltaP}{\Deltat}}N}F=deltaP/deltat*n - суммарная сила взаимодействия частиц со стенкой, то подставив соответствующие значения получим {\displaystylep={\frac {1}{3}}m_{0}nv^{2}}p=1/2m0nv*nv,

так как Ek=1/2mv*v{\displaystyle {\bar {E_{k}}}={\frac {1}{2}}m{\bar {v^{2}}}} , то {\displaystylep={\frac {2}{3}}n{\bar {E_{k}}}}p=2/3nEk

39.

Соотношение

p = nkT,

связывающее давление газа с его температурой и концентрацией молекул, получено в §3.2 для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

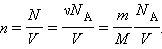Здесь N – число молекул в сосуде, N_А – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

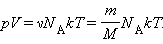Произведение постоянной Авогадро N_А на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть:

R = 8,31 Дж/моль·К.

Соотношение

(*)

называется уравнением состояния идеального газа.

40.

1.1 ОСНОВНЫЕ ПОНЯТИЯ ТЕРМОДИНАМИКИ

Термодинамическая система – тело или группа тел, находящихся во взаимодействии, мысленно или реально обособленные от окружающей среды.

Гомогенная система – система, внутри которой нет поверхностей, разделяющих отличающиеся по свойствам части системы (фазы).

Гетерогенная система – система, внутри которой присутствуют поверхности, разделяющие отличающиеся по свойствам части системы.

Фаза – совокупность гомогенных частей гетерогенной системы, одинаковых по физическим и химическим свойствам, отделённая от других частей системы видимыми поверхностями раздела.

Изолированная система – система, которая не обменивается с окружающей средой ни веществом, ни энергией.

Закрытая система – система, которая обменивается с окружающей средой энергией, но не обменивается веществом.

Открытая система – система, которая обменивается с окружающей средой и веществом, и энергией.

Совокупность всех физических и химических свойств системы характеризует её термодинамическое состояние. Все величины, характеризующие какое-либо макроскопическое свойство рассматриваемой системы – параметры состояния. Опытным путем установлено, что для однозначной характеристики данной системы необходимо использовать некоторое число параметров, называемых независимыми; все остальные параметры рассматриваются как функции независимых параметров. В качестве независимых параметров состояния обычно выбирают параметры, поддающиеся непосредственному измерению, например температуру, давление, концентрацию и т.д. Всякое изменение термодинамического состояния системы (изменения хотя бы одного параметра состояния) есть термодинамический процесс.

Обратимый процесс – процесс, допускающий возможность возвращения системы в исходное состояние без того, чтобы в окружающей среде остались какие-либо изменения.

Равновесный процесс – процесс, при котором система проходит через непрерывный ряд равновесных состояний.

Энергия – мера способности системы совершать работу; общая качественная мера движения и взаимодействия материи. Энергия является неотъемлемым свойством материи. Различают потенциальную энергию, обусловленную положением тела в поле некоторых сил, и кинетическую энергию, обусловленную изменением положения тела в пространстве.

Внутренняя энергия системы – сумма кинетической и потенциальной энергии всех частиц, составляющих систему. Можно также определить внутреннюю энергию системы как её полную энергию за вычетом кинетической и потенциальной энергии системы как целого.

Формы перехода энергии от одной системы к другой могут быть разбиты на две группы. В первую группу входит только одна форма перехода движения путем хаотических столкновений молекул двух соприкасающихся тел, т.е. путём теплопроводности (и одновременно путём излучения). Мерой передаваемого таким способом движения являетсятеплота. Теплота есть форма передачи энергии путём неупорядоченного движения молекул. Во вторую группу включаются различные формы перехода движения, общей чертой которых является перемещение масс, охватывающих очень большие числа молекул (т.е. макроскопических масс), под действием каких-либо сил. Таковы поднятие тел в поле тяготения, переход некоторого количества электричества от большего электростатического потенциала к меньшему, расширение газа, находящегося под давлением и др. Общей мерой передаваемого такими способами движения является работа – форма передачи энергии путём упорядоченного движения частиц.

Теплота и работа характеризуют качественно и количественно две различные формы передачи движения от данной части материального мира к другой. Теплота и работа не могут содержаться в теле. Теплота и работа возникают только тогда, когда возникает процесс, и характеризуют только процесс. В статических условиях теплота и работа не существуют. Различие между теплотой и работой, принимаемое термодинамикой как исходное положение, и противопоставление теплоты работе имеет смысл только для тел, состоящих из множества молекул, т.к. для одной молекулы или для совокупности немногих молекул понятия теплоты и работы теряют смысл. Поэтому термодинамика рассматривает лишь тела, состоящие из большого числа молекул, т.е. так называемые макроскопические системы.

41.

Изотермический процесс (T = const)

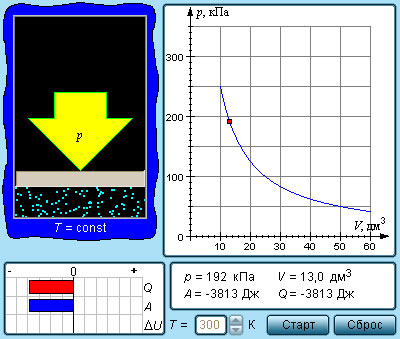
Изотермическим процессом называют квазистатический процесс, протекающий при постоянной температуре T. Из уравнения (*) состояния идеального газа следует, что при постоянной температуре T и неизменном количестве вещества ν в сосуде произведение давления p газа на его объем V должно оставаться постоянным:

pV = const.

Модель. Изотермический процесс

На плоскости (p, V) изотермические процессы изображаются при различных значениях температуры T семейством гипербол p ~ 1 / V, которые называются изотермами. Так как коэффициент пропорциональности в этом соотношении увеличивается с ростом температуры, изотермы, соответствующие более высоким значениям температуры, располагаются на графике выше изотерм, соответствующих меньшим значениям температуры (рис. 3.3.1). Уравнение изотермического процесса было получено из эксперимента английским физиком Р. Бойлем (1662 г.) и независимо французским физиком Э. Мариоттом(1676 г.). Поэтому это уравнение называют законом Бойля–Мариотта.

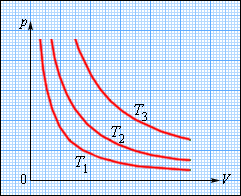Рисунок 3.3.1. Семейство изотерм на плоскости (p, V). T3 > T2 > T1

Изохорный процесс (V = const)

Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным.

Как следует из уравнения (*) состояния идеального газа, при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p ~ T или

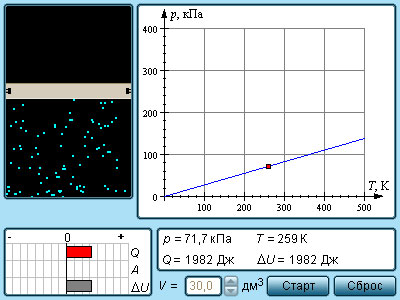Модель. Изохорный процесс

На плоскости (p, T) изохорные процессы для заданного количества вещества ν при различных значениях объема V изображаются семейством прямых линий, которые называются изохорами. Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур (рис. 3.3.2).

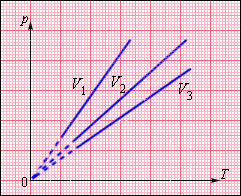Рисунок 3.3.2. Семейство изохор на плоскости (p, T). V3 > V2 > V1

Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Поэтому уравнение изохорного процесса называется законом Шарля.

Уравнение изохорного процесса может быть записано в виде:

где p₀ – давление газа при T = T₀ = 273,15 К (т. е. при температуре 0 °С). Коэффициент α, равный (1/273,15) К^–1, называют температурным коэффициентом давления.

Изобарный процесс (p = const)

Изобарным процессом называют квазистатический процесс, протекающий при неизменным давлении p.

Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид:

где V₀ – объем газа при температуре 0 °С. Коэффициент α равен (1/273,15) К^–1. Его называют температурным коэффициентом объемного расширения газов.

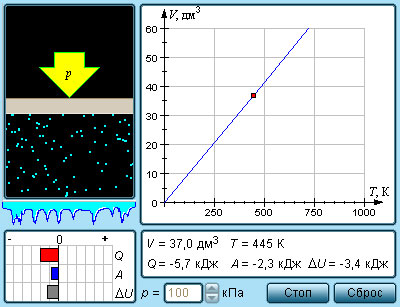Модель. Изобарный процесс

На плоскости (V, T) изобарные процессы при разных значениях давления p изображаются семейством прямых линий (рис. 3.3.3), которые называются изобарами.

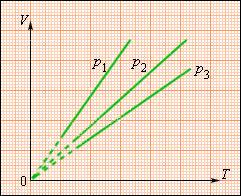Рисунок 3.3.3. Семейство изобар на плоскости (V, T). p3 > p2 > p1

Зависимость объема газа от температуры при неизменном давлении была экспериментально исследована французским физиком Ж. Гей-Люссаком (1862 г.). Поэтому уравнение изобарного процесса называют законом Гей-Люссака.

Экспериментально установленные законы Бойля–Мариотта, Шарля и Гей-Люссака находят объяснение в молекулярно-кинетической теории газов. Они являются следствием уравнения состояния идеального газа.

42.