Фотофизические свойства п.п. лазеров

1. Энергетические состояния.

Волновую функцию электрона в зоне можно записать в виде волновой функции Блоха:

где обладает той периодичностью, что и кристаллическая решетка, а постоянная распространения kс импульсом электронаpизвестным соотношением

Для кристалла в форме параллелепипеда с размерами L_x, L_y, L_z вектор k квантуется: k_i=2pl/L_i, где i=x,y,z, а l-- целое число.

Если блоховскую волновую функцию подставить в уравнение Шрёдингера, описывающее движение электрона в п.п., то окажется, что разрешенные значения энергии электронов попадают в зоны, среди которых верхняя заполненная зона называется валентной, а более высокая пустая - зоной проводимости. Появление зонной структуры связано с дифракцией Брэгга блоховской волновой функции на периодическом кристаллическом потенциале.

В пределах каждой зоны разрешенные значения энергии в приближении параболической зоны:

E_c(k)=h²k²/2m_c - для зоны проводимости,

E_v(k)=h²k²/2m_v - для валентной зоны (от верхушки вниз).

На рисунке изображен случай прямозонного полупроводника.

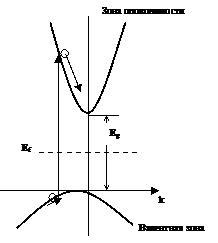
2. Заполнение уровней при тепловом равновесии.

Рассматривая заполнение энергетических уровней необходимо учесть, что волновая функция электрона распространяется на весь кристалл, и что здесь можно применить принцип Паули. Вероятность заполнения уровней в зонах дается статистикой Ферми - Дирака. Таким образом,

f(E)={1+exp[(E-E_f)/kT]}^-1

E_f - этот уровень представляет собой границу между полностью заполненными и пустыми уровнями при 0 К. В невырожденных полупроводниках уровень Ферми располагается внутри запрещенной зоны.

3. Излучательные и безызлучательные переходы.

Если энергия фотона больше ширины запрещенной зоны, то п.п. будет поглощать электромагнитную волну. В случае прямого перехода должен сохраняться полный импульс

k_v+k_опт=k_c

где k_v, k_c - волновые векторы электрона в валентной зоне и зоне проводимости, а k_опт - волновой вектор падающей волны. В оптическом диапазоне k_опт ~10⁵ см^-1, в то время как k_v, k_c имеют порядок 10⁸ см^-1. Можно принять k_опт ~ 0. На диаграмме переход соответствует вертикальной линии. У непрямозонного п.п. минимум зоны проводимости и вершина валентной зоны находятся при разных k.В этом случае переход между указанными двумя состояниями происходит только при участии фонона решетки, чтобы компенсировать изменение импульса кристалла.

Электроны, заброшенные в зону проводимости, релаксируют на дно безызлучательно за время < 100 фс, так же релаксируют дырки к потолку валентной зоны. Рекомбинация электрона и дырки происходит излучательно или безызлучательно. Время жизни для межзонных переходов около 1 нс.

4. Квазиуровни Ферми.

Рассмотрим случай, когда из валентной зоны в зону проводимости заброшено много электронов (или п.проводник очень сильно легирован). Внутри зоны сразу (< 100 фс) установится тепловое равновесие, хотя п.п. как целое и не находится в равновесии. Поэтому можно по отдельности говорить о вероятности заполнения для валентной зоны f_v и зоны проводимости f_c.. Считая при этом

f_v={1+exp[(E-E_fv)/kT]}^-1

f_c={1+exp[(E-E_fc)/kT]}^-1,

где E_fv и E_fc - энергии т.н. квазиуровней Ферми соответственно валентной и зоны проводимости. Достаточно лишь одной этой величины для описания вероятности заполнения большого числа участвующих в генерации уровней.

Получим условие лазерной генерации. Для этого число актов вынужденного излучения должно быть больше числа актов поглощения (для компенсации потерь в резонаторе). Оба указанных процесса пропорциональны числу фотонов в резонаторе q, вероятности перехода B. Вероятность вынужденного излучения будет пропорциональна также произведению вероятности заполнения верхнего уровня f_c(E₂) и вероятности того, что нижний уровень будет свободен (1- f_v(E₁)). Вероятность поглощения пропорциональна произведению вероятности заполнения нижнего уровня f_v(E₁) и вероятности того, что верхний уровень окажется свободным (1- f_c(E₂)). Таким образом, чтобы получить вынужденное излучение на переходе E₂ (зона проводимости) - E₁ (валентная зона), должно выполниться условие

Bq{f_c(E₂)[ 1- f_v(E₁)]- f_v(E₁)[ 1- f_c(E₂)]}>0,

т. е. f_c(E₂) > f_v(E₁).

Из этого неравенства с учетом выражений для f_v f_c получаем

E_fc - E_fv > E₂ - E₁ =hn.

Данное соотношение справедливо при любой температуре пока остается применимым понятие квазиуровней Ферми. Это условие - результат требования того, чтобы процессы вынужденного излучения преобладали над процессами поглощения. Заметим, что энергия излучаемого фотона должна, очевидно, быть больше ширины запрещенной зоны. Таким образом, мы приходим к условию:

E_g < hn < E_fc - E_fv,

которое приблизительно устанавливает ширину контура усиления п.п.

Заметим, чтобы выполнилось неравенство E_g < E_fc - E_fv, число заброшенных в зону проводимости электронов должно превысить некоторое критическое значение. До тех пор, пока не будет достигнут этот минимальный уровень инжекции, усиление в полупроводнике не наблюдается.