Время жизни фотона и добротность резонатора
Попытаемся вычислить скорость релаксации энергии в резонаторе для определенной моды. Рассмотрим для простоты плоскопараллельный резонатор. Моду резонатора можно представить как суперпозицию падающей и отраженной волн. Введем обозначения: I0 – начальная интенсивность падающей волны, R1, R2 – коэффициенты отражения по мощности двух зеркал, Ti – относительные внутренние потери за проход. Интенсивность I(t1) после одного полного прохода в момент времени 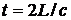 запишется в виде
запишется в виде
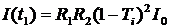
Интенсивность после m проходов, т.е. в момент времени
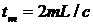 ,
,
равна
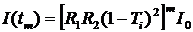 .
.
Если q(t) – полное число фотонов в резонаторе в момент времени t, то оно пропорционально интенсивности, т.е. 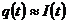 . И тогда можно записать
. И тогда можно записать
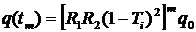 ,
,
где q0 – начальное число фотонов в резонаторе. Следовательно, число фотонов в момент времени tm равно:
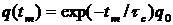 .
.
Сравнение двух последних выражений показывает, что (с учетом 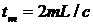 )
)
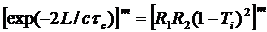 .
.
Откуда находим
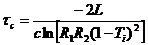 . (3.12)
. (3.12)
Если предполагать, что экспоненциальная зависимость q(tm) справедлива в любой момент времени t, то можно написать
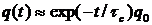 ,
,
здесь τс – время жизни фотона, определяемое выражением (3.12).
Например, R1=R2=R=0,98; Ti≈0, то из (*) получим τс=49,5L/c. Видно, что время жизни фотона много больше времени одного прохода резонатора. Если положить L=90 см и с=с0, то получим tT≈3 нс и τс≈150 нс.
При условии, что 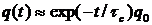 справедливо, временную зависимость электрического поля можно представить в виде
справедливо, временную зависимость электрического поля можно представить в виде 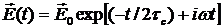 . С помощью фурье-преобразования доказывается, что спектр мощности излучения имеет лоренцеву форму линии с полушириной
. С помощью фурье-преобразования доказывается, что спектр мощности излучения имеет лоренцеву форму линии с полушириной
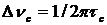 .
.
Следует отметить, что спектр излучения не совпадает со спектром пропускания. Однако расхождения между числовыми результатами совсем невелики. Одна из причин такого расхождения состоит в том, что было принято условие 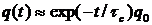 .
.
Добротность
Для любой резонансной системы Q=2π(запас. эн.)/(эн. тер. за цикл). Запасенная энергия qhν, теряемая 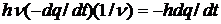 , и имеем
, и имеем
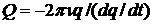 ,
,
с учетом 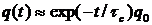 находим
находим 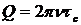
и, учитывая еще 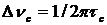 , получаем
, получаем  .
.
Для конкретных значений τс≈150 нс и ν=5·1014 Гц (λ=0,6мкм) Q=4,7·108.
Глава 4. Режимы работы лазеров
Теория основывается на приближении скоростных уравнений. Соответствующие уравнения выводятся из условия баланса между скоростями изменения полного числа частиц и полного числа фотонов лазерного излучения. Такой подход дает простое и наглядное описание работы лазера.
Скоростные уравнения
Четырехуровневый лазер
Рассмотрим четырехуровневую схему. Полагаем, что накачка проводится в одну полосу поглощения, релаксация из этой полосы на верхний лазерный уровень 2 происходит очень быстро, также быстро происходит релаксация и с 1 уровня на основной.

Обозначим населенности четырех уровней 0, 1, 2 и 3 соответственно через Ng, N1, N2 и N3. Будем считать, что лазер генерирует только на одной моде резонатора. Пусть q – полное число фотонов в резонаторе. Считаем, что переходы 3 – 2 и 1 – 0 являются быстрыми, поэтому можно положить N1≈N3≈0. В этом случае имеем следующие скоростные уравнения:
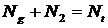 (4.1)
(4.1)
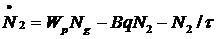 (4.2)
(4.2)
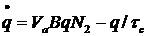 , (4.3)
, (4.3)
где Nt – полное число активных атомов. Второе уравнение дает изменение числа частиц на верхнем лазерном уровне. Уравнение 4.3 определяет скорость изменения числа фотонов в резонаторе: первый член дает увеличение числа фотонов вследствие вынужденного излучения (Va – объем, занимаемый модой внутри активной среды), второй – учитывает уменьшение числа фотонов из-за потерь в резонаторе (τс – время жизни фотона).
Следует заметить, что в выражении 4.3 нет слагаемого, учитывающего спонтанное излучение. В действительности генерация возникает за счет спонтанного излучения. Если в уравнениях положить q=0 в момент t=0, то получим 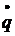 =0, и генерация не сможет возникнуть. Правильное выражение для члена, учитывающего спонтанное излучение, получается из квантовомеханического рассмотрения электромагнитного поля моды резонатора. В случае, когда учитывается спонтанное излучение, уравнение 4.3 преобразуется к виду:
=0, и генерация не сможет возникнуть. Правильное выражение для члена, учитывающего спонтанное излучение, получается из квантовомеханического рассмотрения электромагнитного поля моды резонатора. В случае, когда учитывается спонтанное излучение, уравнение 4.3 преобразуется к виду:


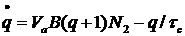 .
.
Однако для простоты мы не будем вводить такого дополнительного члена, а предположим, что в резонаторе уже имеется небольшое число фотонов qi. Это небольшое число фотонов, которое необходимо для возникновения генерации, в действительности не сказывается на последующем рассмотрении.
Далее получим приближенное значение для величины B, которое подходит для большинства практических приложений. Моду рассматриваем как суперпозицию падающей и отраженной волн, также вводим сечение перехода на частоте моды σ. Изменение интенсивности дается выражением:



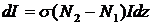 .
.
А за полный проход
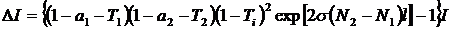
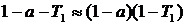
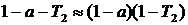
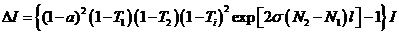 , (4.6)
, (4.6)
αi – потери в зеркалах, Тi – пропускание зеркал, Тi – внутренние потери.
Введем новые величины γ, которые можно представить как логарифмические потери за проход, а именно:
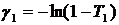
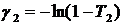 (4.7)
(4.7)
 .
.
А полные потери (потери пропускания зеркал γ 1 и γ2 плюс внутренние потери γi) за проход γ определим так:
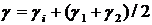 (4.8)
(4.8)
Подставим (4.7) и (4.8) в (4.6) и введем дополнительное условие
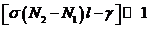 (4.9)
(4.9)
Последнее условие позволяет разложить экспоненту (4.6) в степенной ряд:
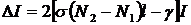
Разделим обе части этого выражения на Δt, за которое световая волна совершает полный проход резонатора, т.е. на 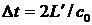 , где
, где 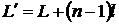 оптическая длина пути. Используя приближение
оптическая длина пути. Используя приближение 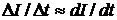 , получаем:
, получаем:
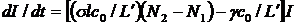 . (4.10)
. (4.10)
Поскольку число фотонов в резонаторе пропорционально интенсивности света полученное уравнение можно сравнить с уравнением
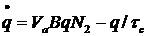
Из этого сравнения получим следующие выражения:
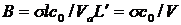
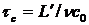 , (4.11)
, (4.11)
где 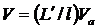 .
.
Несколько замечаний к проведенному рассмотрению.
--При выводе уравнения для 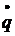
 мы использовали приближение, согласно которому разница между потерями и усилением невелика. Для непрерывного лазера это всегда выполняется, поскольку в установившемся процессе
мы использовали приближение, согласно которому разница между потерями и усилением невелика. Для непрерывного лазера это всегда выполняется, поскольку в установившемся процессе 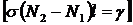 .
.
--Для импульсного лазера это условие применимо, когда лазер работает при малом превышении над порогом.
--Для импульсного лазера динамическое поведение следует анализировать проход за проходом.
Скоростные уравнения принято записывать через инверсию населенностей:
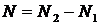
В силу предположения, что релаксация с уровня 1 является быстрой, имеем 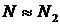 , и исходные уравнения нетрудно свести к двум уравнениям:
, и исходные уравнения нетрудно свести к двум уравнениям:
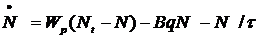
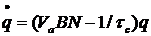
Для количественного описания работы лазера необходимо решить эти уравнения с учетом начальных условий. Если t=0, то N(0)=0, а q(0)=qi, где qi – малое число изначально присутствующих фотонов, стимулирующих вынужденное излучение. Из (4.11) и (4.8) следует:
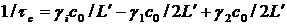
Если это выражение подставить в (4.3), то понятно, что величина 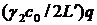 представляет собой скорость ухода фотонов из резонатора через второе зеркало. Следовательно, выходная мощность будет равна:
представляет собой скорость ухода фотонов из резонатора через второе зеркало. Следовательно, выходная мощность будет равна:

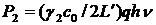
Следует отметить, что полученные результаты применимы только в случае одномодовой генерации.
Трехуровневый лазер
Предполагаем, что имеется лишь одна полоса поглощения накачки, и переход 3→2 быстрый, тогда можно положить N3≈0.
При этом можно записать скоростные уравнения:

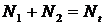
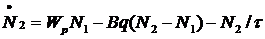
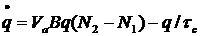
Используя равенство 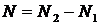 можно записать
можно записать
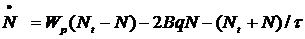
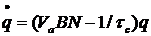
Эти уравнения совместно с выражениями
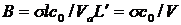
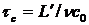 ,
,
где 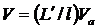 , описывают как установившееся, так и динамическое поведение трехуровневого лазера (аналогично 4-хуровнему). Однако скоростные уравнения для инверсии населенностей отличаются. Член, отвечающий вынужденному излучению, отличается на коэффициент 2. Это связано с тем, что при излучении одного фотона в трехуровневом лазере инверсия населенностей изменяется на 2 (N2 уменьшается на 1, а N1 увеличивается на 1), а в 4-хуровневом на 1(N2 уменьшается на 1, а N1 остается ≈0 из-за быстрой релаксации).
, описывают как установившееся, так и динамическое поведение трехуровневого лазера (аналогично 4-хуровнему). Однако скоростные уравнения для инверсии населенностей отличаются. Член, отвечающий вынужденному излучению, отличается на коэффициент 2. Это связано с тем, что при излучении одного фотона в трехуровневом лазере инверсия населенностей изменяется на 2 (N2 уменьшается на 1, а N1 увеличивается на 1), а в 4-хуровневом на 1(N2 уменьшается на 1, а N1 остается ≈0 из-за быстрой релаксации).
