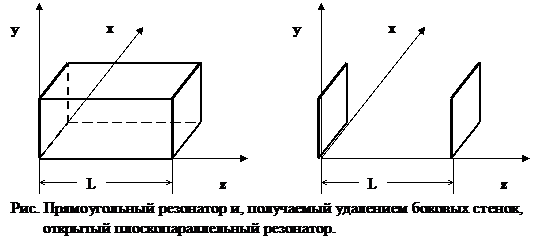
Плоскопараллельный резонатор

Рассмотрим прямоугольную полость с идеально проводящими стенками, полностью заполненную диэлектриком. Вычислим распределение стоячих электромагнитных волн, которое может существовать в этой полости. Согласно уравнениям Максвелла, напряженность электрического поля E(x,y,z,t) должна удовлетворять волновому уравнению

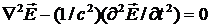, (3.2)

где 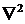- оператор Лапласа, а с – скорость света в рассматриваемой среде. Кроме того, напряженность электрического поля должна удовлетворять следующему граничному условию на каждой стенке

,

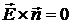где n – нормаль к поверхности рассматриваемой стенки. Это условие выражает тот факт, что тангенциальная компонента электрического поля должна обращаться в нуль на стенках полости.

Задача решается разделением переменных. Таким образом, записывая

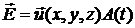(3.4)

и подставляя это выражение в (2.2), получаем

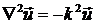(3.5а)

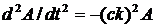, (3.5б)

где k – постоянная величина. Уравнение (2.5б) имеет общее решение

,

где А₀ и φ – произвольные постоянные величины, а ω=ck.

При гармоническом виде функции А(t), решение (2.4) соответствует определенной конфигурации стоячей волны электромагнитного поля внутри полости. Решение такого типа называется модой резонатора. Решения уравнения Гельмгольца (2.5а) с учетом граничных условий имеют вид:

,

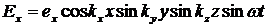
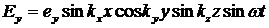
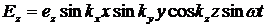где 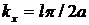, , 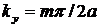, 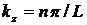а резонансные частоты даются выражением

(3.6)

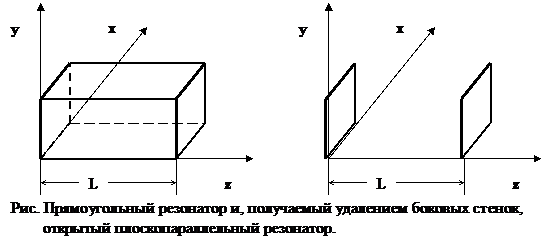Моды открытого резонатора с хорошей точностью описываются модами прямоугольного резонатора, для которых (l,m)<<n. Это можно аргументировать тем, что при (l,m)<<n волны распространяются под очень малыми углами к оси z. И можно ожидать, что отсутствие боковой поверхности не скажется заметным образом на этих модах. Резонансные частоты плоскопараллельного резонатора можно найти разложением (3.6) в ряд:

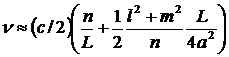
Из этого выражения можно получить разность частот между двумя продольными модами 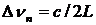, или поперечными

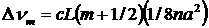
Интерферометр Фабри-Перо

Интерферометр Фабри – Перо состоит из двух плоских и параллельных друг другу зеркал. При пропускании света в нем происходит многократная интерференция. Большая популярность этого прибора объясняется как минимум тремя причинами: 1) физические процессы, происходящие в нем, на фундаментальном уровне аналогичны тем, что имеют место в оптических резонаторах; 2) во многих случаях его применяют для селекции частот внутри лазерного резонатора; 3) его используют для анализа спектров, включая лазерное излучение.

Как уже отмечалось, интерферометр Фабри – Перо состоит из двух плоских и параллельных друг другу зеркал с коэффициентом отражения по мощности R₁, R₂. Эти зеркала разделены диэлектрическим промежутком (показатель преломления n_r) длиной L. На интерферометр падает плоская волна под углом Θ₁. Выходной пучок представляет собой суперпозицию многих пучков, возникающих из-за многократных отражений.

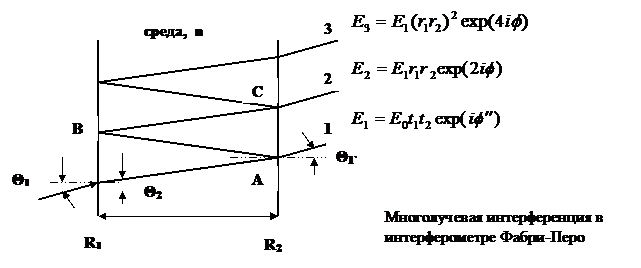
Амплитуда электрического поля выходного пучка E_t получается суммированием амплитуд всех выходных пучков с учетом фаз. Если учесть все многократные отражения, то получим

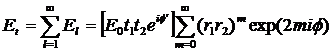(1)

В этом выражении: E₀ – амплитуда пучка, падающего на интерферометр; t₁ и t₂ – коэффициенты пропускания обоих зеркал для электрического поля; r₁ и r₂ – коэффициенты отражения для электрического поля; 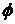¹ – фазовый набег при однократном прохождении, включающий в себя также и набеги фазы при прохождении обоих зеркал; 2 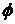- сдвиг фазы между последовательными отражениями, равный

,

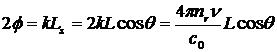здесь L_S – сумма длин двух отрезков AB и BC, а угол θ связан с θ¹ ( 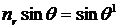). Сумма геометрической последовательности (1) равна

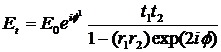
Коэффициент пропускания Т интерферометра по мощности равен просто 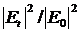, и из предыдущей формулы находим

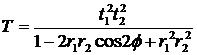. (3.7)

Поскольку 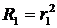, , 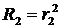а для зеркала без потерь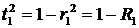 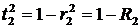, то с учетом этих соотношений выражение (3.7) преобразуется к виду:

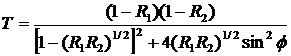(3.8)

Это и есть результат наших вычислений. Свойства интерферометра Фабри-Перо иллюстрирует рис. , на котором изображена зависимость пропускания Т интерферометра от частоты ν падающей волны.

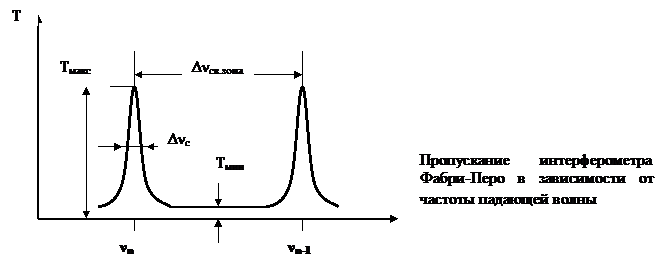
Кривая пропускания T(ν) построена по формуле (3.8) с учетом 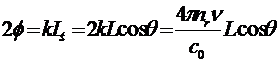. Кривая состоит из последовательности максимумов. Максимумы наблюдаются при sin²φ=0, т.е. при φ=nπ. Частоты, соответствующие максимумам, равны 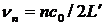. Интервал между двумя соседними максимумами называется свободной спектральной зоной.

Максимальное пропускание .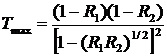

Минимальное пропускание .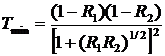

Например, при R₁=R₂=0,98 T_min≈10^-4.

Ширина пика пропускания определяется из условия, что «боковая мощность» равна половине максимальной. T_1/2=0,5T_max. Тогда из формулы (3.8) получаем

.

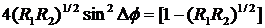Далее, при малых 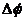можно считать 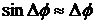, тогда из последнего выражения получим

,

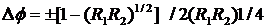и ширина полосы пропускания

.

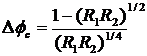Важной характеристикой интерферометра является ширина свободной зоны в единицах ширины полосы пропускания, т.н. резкость интерферометра

.

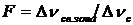
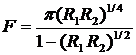Резкость интерферометра показывает, насколько узка линия пропускания по сравнению со свободной зоной (зоной дисперсии). Резкость интерферометра определяет его разрешающую способность.