Основные формулы и указания к решению задачи

7.1.1. Переменный ток, текущий через резистор сопротивлениемR

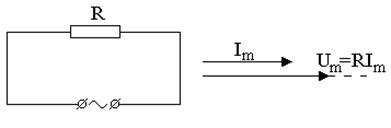
Если к концам участка цепи (рис. 7.1а) приложено напряжение U = U_m сos wt, то сила тока определяется законом Ома I = U/R = (U_m/R) сos wt = = I_m сos wt, где I – амплитуда силы тока. Векторная диаграмма (рис. 7.1б) амплитудных значений тока I_m и напряжения U_m на резисторе показывает, что сдвиг фаз между I_m и U_m равен нулю.

А б

Рис. 7.1. Схема цепи переменного тока (а) и

векторная диаграмма, соответствующая данной цепи (б).

7.1.2. Переменный ток, текущий через катушку индуктивностьюL

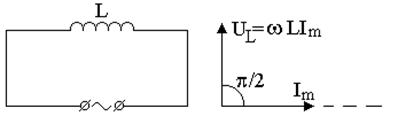
Если в цепи (рис. 7.2а)приложено переменное напряжение U = U_m сos wt, то сила тока в такой цепи I = I_m сos (wt – p/2). Величина R_L = wL называется индуктивным сопротивлением. Векторная диаграмма (рис. 7.2б) показывает, что падение напряжения U опережает по фазе ток I, текущий через катушку на p/2.

А б

Рис. 7.2. Схема цепи переменного тока (а) и

векторная диаграмма, соответствующая данной цепи (б).

Переменный ток, текущий через конденсатор емкостью С

Если переменное напряжение приложено к конденсатору (рис. 7.3а), то он все время перезаряжается, и в цепи течет переменный ток. Если все внешнее напряжение приложено к конденсатору, а сопротивлением подводящих проводов можно пренебречь, то U = U_m сos wt. Сила тока I = I_m сos(wt + p/2), где I_m = U_m/(1/(wC)).

Величина R_C = 1/(wC) называется емкостным сопротивлением.

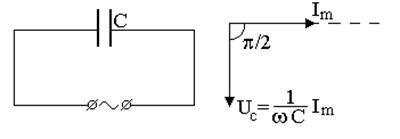
Падение напряжения на конденсаторе U отстает по фазе от текущего через конденсатор тока I на p/2. Это показано на векторной диаграмме (рис. 7.3б).

А б

Рис. 7.3. Схема цепи переменного тока (а) и

векторная диаграмма, соответствующая данной цепи (б).

Цепь переменного тока, содержащая последовательно включенные резистор, катушку индуктивности и конденсатор

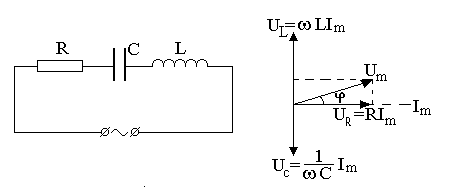
Рассмотрим цепь переменного тока, содержащую последовательно включенные резистор, катушку и конденсатор (рис. 7.4а).На рис. 7.4б представлена векторная диаграмма амплитуд падений напряжений на резисторе (U_R), катушке (U_L) и конденсаторе (U_C). Амплитуда U_m приложенного напряжения должна быть равна векторной сумме амплитуд этих падений напряжений. Угол j определяет разность фаз между напряжением и силой тока

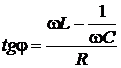. (7.1)

Из прямоугольного треугольника получаем

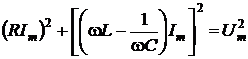, (7.2)

откуда амплитуда силы тока имеет значение

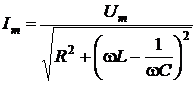. (7.3)

Следовательно, если напряжение в цепи изменяется по закону

U = U_m сos wt, то в цепи течет ток I = I_m сos(wt – j).

А б

Рис. 7.4. Схема цепи переменного тока (а) и

векторная диаграмма, соответствующая данной цепи (б).

Действующие значения тока и напряжения для синусоидального тока соответственно равны:

I = I_m / 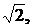U = U_m / 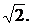(7.4)

Примеры решения задач

Пример 1. В цепи переменного тока (f = 50 Гц) с действующим напряжением 127 В включены параллельно конденсатор емкостью C = 24 мкФ и дроссель индуктивностью L = 0,6 Гн и активным сопротивлением R = 100 Ом. Определите действующее значение подводимого к участку тока.

Дано: U = 127 В; f = 50 Гц; C = 24×10^-6 Ф; L = 0,6 Гн; R = 100 Ом.

I = ?

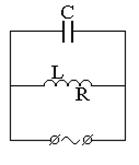
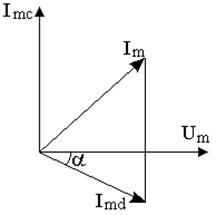
Решение.Начертим схему соединения приборов (рис. 7.5а) и построим векторную диаграмму токов (рис. 7.5б). При параллельном соединении элементов на каждом из них напряжение одинаковое, поэтому за основное направление возьмем вектор амплитуды напряжения.

а	б

Рис. 7.5. Схема цепи переменного тока (а) и

векторная диаграмма, соответствующая данной цепи (б).

Амплитуда тока в конденсаторе I_mС опережает амплитуду напряжения на p/2, амплитуда тока в дросселе I_md отстает от амплитуды напряжения на угол

. (7.5)

Векторная сумма токов I_mC и I_md определяет подводимый ток I. Из векторной диаграммы очевидно, что

I ²_m = I ²_mC + I ²_md – 2×I_mC I_md соs(90 – a) = I ²_mC + I ²_m – 2 I_mC I_md sin a. (7.6)

Перейдем к действующим значениям тока:

I ² = I ²_C + I ²_d – 2×I_C I_d sin a, 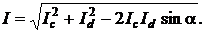(7.7)

Токи I_C и I_d найдем, применив закон Ома к каждому участку отдельно:

I_C = UwC, 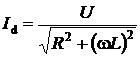, w = 2pf. (7.8)

Расчеты дают: sina = 0,8832; I_C = 0,96 A, I_d = 0,562 A; I = 0,515 A.

Выполним проверку единиц измерения величин.

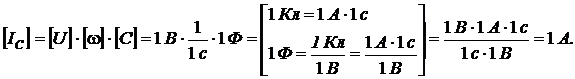(7.9)

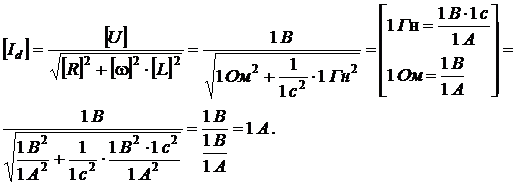
Пример 2. В цепь переменного тока (f = 50 Гц) с действующим значением силы тока 10 А включены последовательно конденсатор емкостью C = 18 мкФ, активное сопротивление R₁ = 10 Ом и дроссель индуктивностью L = 0,6 Гн и активным сопротивлением R₂ = 109 Ом. Определить действующее в цепи напряжение.

Дано: f = 50 Гц; I = 10 А; C = 18×10^-6 мкФ; R₁ = 10 Ом; L = 0,6 Гн; R₂ = 100 Ом.

U – ?

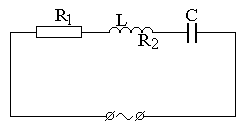
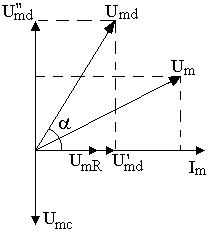
Решение.Начертим схему включения приборов (рис. 7.6 а) и построим векторную диаграмму напряжений (рис. 7.6 б).

а	б

Рис. 7.6 Схема цепи переменного тока (а) и

векторная диаграмма соответствующая данной цепи (б).

При последовательном соединении через все элементы идет одинаковый ток, поэтому за основное направление возьмем вектор амплитуды тока I_m. Амплитуда напряжения на конденсаторе U_mC отстает по фазе от тока на p/2. Амплитуда напряжения на дросселе U_md опережает по фазе ток на a. Амплитуду напряжения на дросселе разложим на две составляющие: активную U'_md = U_md cos a (колеблется в фазе с током) и реактивную U''_md = U_md sin a (опережает ток по фазе на p/2). Амплитуда напряжения на резисторе U_mR совпадает с амплитудой тока (колеблется в фазе с током). Амплитуда полного напряжения в цепи равна векторной сумме напряжений U'_md, U''_md, U_mC и U_mR.

Амплитуда напряжения, совпадающего по фазе с током:

U_1m = U_mR + U'_md = I_mR₁ + I_mR₂. (7.10)

Амплитуда напряжения, опережающего ток на p/2:

U_2m = U''_md – U_mC, 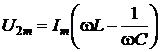. (7.11)

Амплитуда полного напряжения

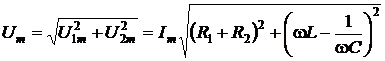. (7.12)

Перейдем к действующим значениям напряжения и тока

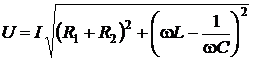, w = 2pf. (7.13)

Подставим численные данные

U = 220 В.

Выполним проверку единиц измерения величин.

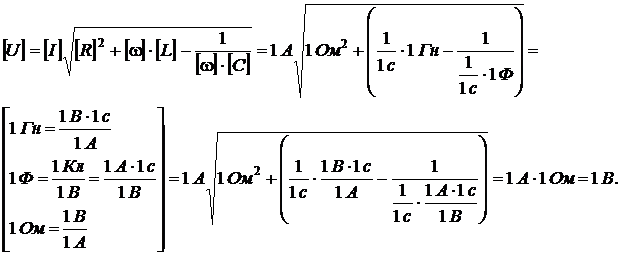
(7.14)

7.3 Задание для самостоятельного выполнения по вариантам

В цепь переменного тока n = 50 Гц с действующим напряжением U и действующим значением подводимого к участку тока I включены, как показано на рис. 7.7 конденсаторы С₁ и С₂, активные сопротивления R₁ и R₂, дроссели с индуктивностью L₁, L₂ и активными сопротивлениями R_L1 и R_L2.

1) Определите величину обозначенную в табл. 7.1 вопросительным знаком.

2) Начертите векторные диаграммы токов и напряжений (на одном рисунке) для схем, изображенных на рис. 7.7.

Значения величин. Таблица 7.1

№ варианта	С1, мкФ	С2, мкФ	L1, Гн	L2, Гн	R1, Ом	R2, Ом	RL1, Ом	RL2, Ом	U, В	I, А
			0,1							?
										?
			0,2							?
			0,3							?
			0,1	0,2						?
			0,2	0,3						?
			0,1	0,3						?
			0,2							?
			0,2						?
			0,1	0,1					?
			0,5	0,4					?
			0,6						?
									?
			0,5	0,5					?
			0,4						?
			0,4						?

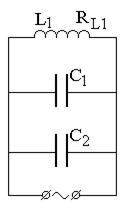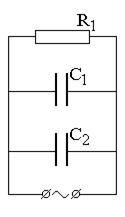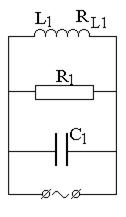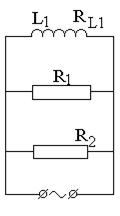вариант 1	вариант 2	вариант 3	вариант 4
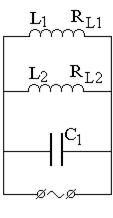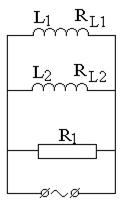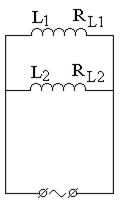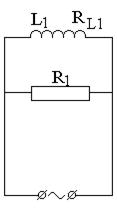вариант 5	вариант 6	вариант 7	вариант 8
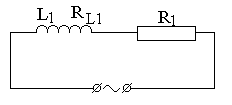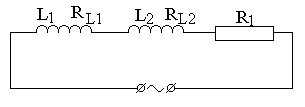вариант 9	вариант 10
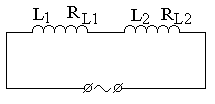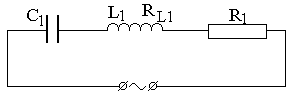вариант 11	вариант 12

Рис. 7.7. Схемы цепей переменного тока

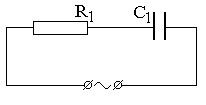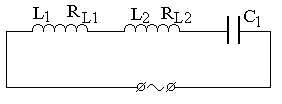вариант 13	вариант 14
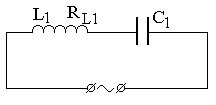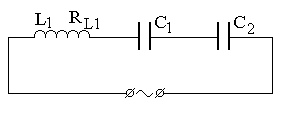вариант 15	вариант 16

Продолжение рис. 7.7. Схемы цепей переменного тока

литература

1. Савельев, И.В. Курс общей физики. Учебное пособие в 3 т. Т. 2./ И.В. Савельев. ‑ М.: Наука, 1988.

2. Зисман, Г.А. Курс общей физики. Учебное пособие в 3 т. Т. 2./ Г.А. Зисман, О.М. Тодес. ‑ М.: Наука, 1979.

3. Детлаф, А.А. Курс физики/ А.А. Детлаф, Б.М. Яворский. Учебное пособие ‑ М.: Высшая школа, 1989.

4. Волькенштейн, В.С. Сборник задач по общему курсу физики / В.С. Волькенштейн. – 6-е изд. стереотипное. ‑ М.: Наука, 1967.

5. Чертов, А.Г. Задачник по физике: учеб. пособие для студентов втузов/ А.Г. Чертов, А.А. Воробьев. ‑ 6-е изд., перераб и доп. ‑ М.: Интеграл-Пресс, 1997.

6. Трофимова, Т.И. Сборник задач по курсу физики с решениями: учеб. пособие для вузов/ Т.И. Трофимова, З.Г. Павлова. – 3-е изд. стереотипное. – М.: Высш. шк., 2002.

Приложение 1