Тема: Сила, действующая на заряд, движущийся в магнитном поле

Основные формулы и указания к решению задачи

Сила, действующая на провод с током в магнитном поле (закон Ампера),

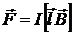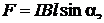
или (5.1)

где l – длина провода;

a – угол между направлением тока в проводе и вектором магнитной индукции .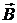

Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять к каждому элементу провода в отдельности:

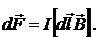(5.2)

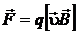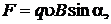Сила Лоренца – или (5.3)

где 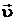– скорость заряженной частицы;

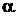– угол между векторам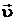и и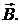

Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора u (если заряд положительный), то отогнутый большой палец покажет направление силы Лоренца.

Отметим, что магнитное поле действует только на движущиеся в нем заряды, на покоящиеся электрические заряды магнитное поле не действует.

Пример решения задачи

Рассмотрев фотографию треков заряженных частиц, двигавшихся в магнитном поле определить отношение заряда к массе неизвестной частицы, а также знак заряда этой частицы, если известно, что левый трек принадлежит ядру атома водорода, правый неизвестной частице. Отношение заряда атома водорода к его массе равно 9,6×10⁷ Кл/кг. Модули начальных скоростей частиц одинаковы. Индукция магнитного поля 2,2 Тл. Направление магнитного поля показано на рис. 5.1.

Решение. Для решения этой задачи оба трека осторожно переносят на кальку или делают ксерокопию рисунка. Затем измеряют радиусы кривизны треков. Для этого вначале находят центры кривизны. В средних участках треков проводят по две хорды и в середине к ним восстанавливают перпендикуляры. Точки пересечения перпендикуляров будут центрами кривизны треков. Затем измеряют радиусы кривизны с помощью измерительной линейки, учитывая масштаб снимка.

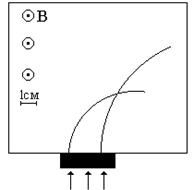
Рис. 5.1. Треки заряженных частиц в магнитном поле

Для нашего случая R₁ = 0,032 м, R₂ = 0,072 м.

На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца, вектор которой перпендикулярен вектору скорости частицы. Эта сила является центростремительной силой:

F_л = quB, 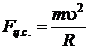, F_л = F_ц.с., (5.4)

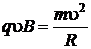. (5.5)

Отсюда модуль скорости неизвестной частицы u₁ будет равен:

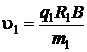, (5.6)

где q₁ – заряд частицы;

m₁ – масса частицы;

R₁ – радиус кривизны трека;

B – модуль магнитной индукции.

Модуль скорости ядра атома водорода u₂ равен:

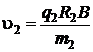, (5.7)

где q₂ – заряд ядра водорода;

m₂ – масса ядра атома водорода;

R₂ – радиус кривизны трека.

Так как по условию u₁ = u₂, то

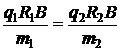. (5.8)

Отсюда получаем:

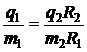. (5.9)

Подставляя в последнюю формулу числовые данные, находим:

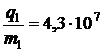Кл/кг.

Выполним проверку единиц измерения величин.

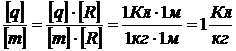. (5.10)

Воспользовавшись правилом левой руки определяем, что наша частица заряжена положительно.

5.3 Задание для самостоятельного выполнения по вариантам

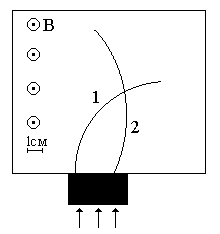
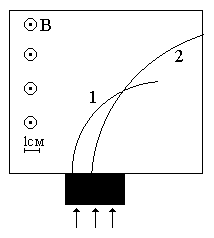
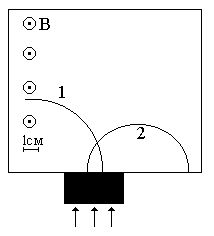
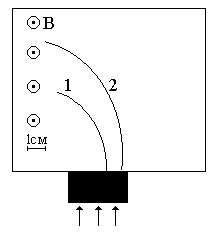
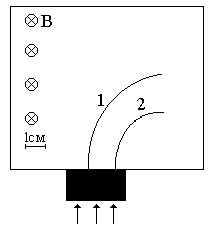
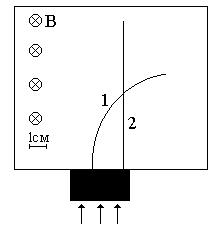
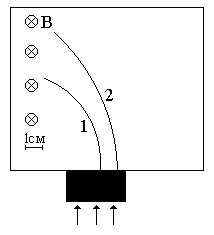
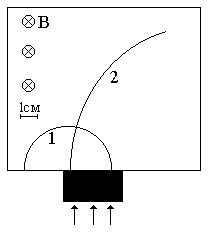
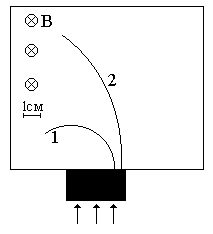
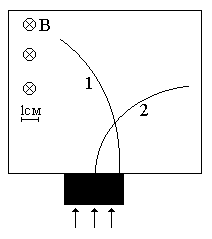
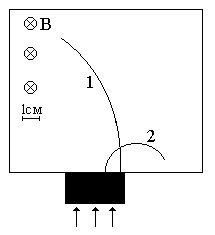
Неизвестные частицы 1 и 2 (см. рис. 5.2) прошли ускоряющую разность потенциалов U и влетели перпендикулярно линиям магнитной индукции В в камеру Вильсона. По фотографии трека определите удельный заряд частиц q/m и укажите знаки их заряда. При измерении радиусов треков учитывайте масштаб снимка, указанный на рис. 5.2. Направление линий магнитной индукции указано на рисунке обозначением:  – перпендикулярно листу бумаги "к нам", Ä – перпендикулярно листу бумаги "от нас". Данные приведены в табл. 5.1.

Таблица 5.1

Значения величин.

№ варианта	U, B	В, Tл
		2,1
		2,2
		2,3
		2,4
		2,5
		2,6
		2,7
		2,8
		2,9
		3,0
		3,1
		3,2
		3,3
		3,4
		3,5

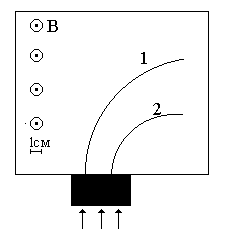вариант 1	вариант 2
вариант 3	вариант 4
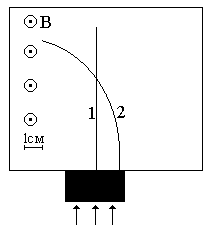вариант 5	вариант 6

Рис. 5.2. Треки частиц в магнитном поле

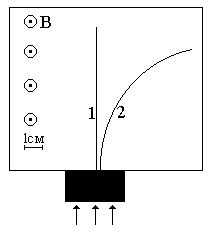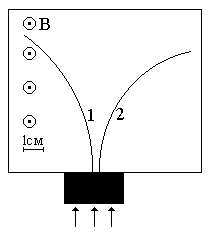вариант 7	вариант 8
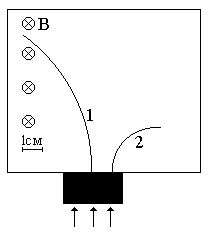вариант 9	вариант 10
вариант 11	вариант 12

Продолжение рис. 5.2. Треки частиц в магнитном поле

вариант 13	вариант 14
вариант 15	вариант 16

Продолжение рис. 5.2. Треки частиц в магнитном поле