Параметры состояния. Законы и уравнения состояния идеальных газов.

Параметры состояния. Законы и уравнения состояния идеальных газов.

1.4; 3.11; 3.15; 3.22; 3.23.

1.4 В машинном зале электростанции работают три турбины, в конденсаторах которых поддерживается абсолютное давление p₁ = 2,94 кПа, р₂ = 3,923 кН/м² и р₃ = 0,711 lbf/in². Определите величины вакуумов в процентах барометрического давления. Показание барометра в машинном зале В = 753 мм рт. ст.

Решение. Давление:

,

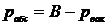где 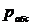- абсолютное давление;

В – барометрическое (атмосферное) давление;

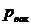- давление разряжения (вакуум).

Тогда 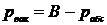. Выражаем все в Па (таблица 5, с. 291, [3]).

1) p₁ = 2,94 кПа = 2940 Па; ; ;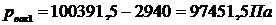

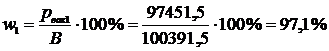2) р₂ = 3,923 кН/м² = 3,923 кПа = 3923 Па; ;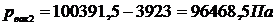

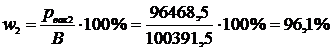
3) 10 lbf/in² = 0,68948·10⁵ Па

0,711 lbf/in² = р₃. р₃ = 4902,2 Па. ;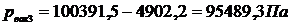

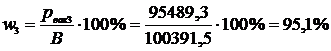
4) 10³ мм рт. ст. = 1,33322·10⁵ Па

753 мм рт. ст. = В. В = 100391,5 Па.

Ответ: , , .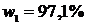

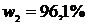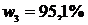3.11 Определите массу воздуха, находящегося в комнате площадью 25 м² и высотой 3,2 м. Принять, что температура воздуха в комнате t = 22⁰С, а барометрическое давление В = 986,5 гПа.

Решение.Уравнение состояния идеальных газов 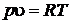, для произвольной массы газа m, кг:

,

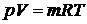где р – абсолютное давление, Па;

V – объем, м³;

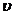- удельный объем, м³/кг;

Т – температура, К;

R – удельная газовая постоянная, Дж/(кг·К).

,

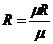где 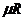- универсальная газовая постоянная, Дж/(кмоль·К).

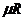= 8314,51 Дж/(кмоль·К)

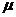- молекулярная масса, кг/ кмоль (таблица 7, с. 292, [3])

Газовая постоянная 1 кг газа R = 8314,51/ .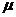

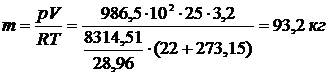
Ответ: 93,2 кг.

3.15 В комнате площадью 35 м² и высотой 3,1 м воздух находится при t = 23⁰C и барометрическом давлении В = 973 гПа. Какое количество воздуха проникнет с улицы в комнату, если барометрическое давление увеличится до В = 1013 гПа. Температура воздуха остается постоянной.

Решение.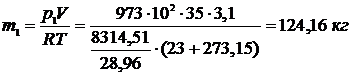

.

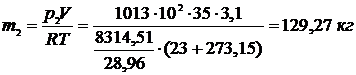
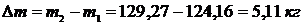Ответ :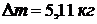

3.22 При температуре t = 800⁰C и давлении р = 0,1 МПа плотность газа 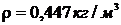. Что это за газ?

Решение. 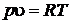, 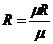→ 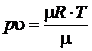, 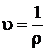.Откуда 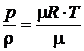. Следовательно,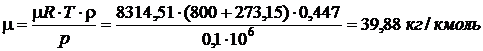

По таблице 7, с. 292 [3] определяем по молекулярной массе, что искомый газ – аргон.

Ответ:аргон.

3.23 Компрессор подает кислород в резервную емкость 3 м 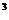. Избыточное давление в резервуаре увеличивается при этом от 0,01 до 0,6 МПа, а температура газа – от 15 до 30 ⁰С. Определите массу поданного компрессором кислорода. Барометрическое давление 993гПа.- гекто

Решение.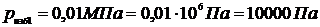

,

,

=

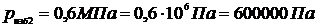
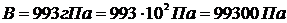
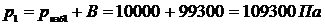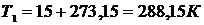
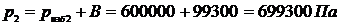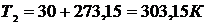
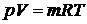
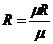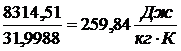
Изначальное количество кислорода, кг, в резервуаре:

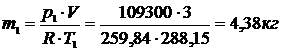
После подачи кислорода компрессором, кг:

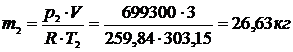
Масса поданного компрессором кислорода:

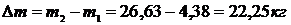
Ответ: .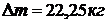

Решение.

1) Используя [5, табл. III, с.47] определяем, что это перегретый пар;

2) Используя [5, табл. II, с.26] определяем

р = 0,4 МПа = 4·10⁵ Па. При этом давлении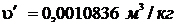

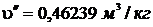
Т.к. 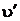< < 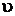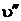, т.е. 0,0010836<0,015<0,46239, то состояние воды – влажный пар.

3) Используя [5, табл. I, с.19] определяем

t = 170⁰С. При этой температуре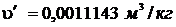

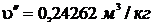
Т.к. 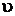< 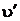, т.е. 0,00105<0,0011143, то состояние воды – жидкость.

4) Используя [5, табл. II, с.31] определяем

р = 18,2 МПа = 1,82·10⁷ Па. При этом давлении t = 357,90⁰С. Поэтому, это может быть состояние кипящей жидкости, влажного пара, сухого насыщенного пара.

Ответ:1) перегретый пар; 2) влажный пар; 3) жидкость; 4) кипящая жидкость, влажный пар, сухой насыщенный пар.

9.5 В сосуде объемом V = 500 см³ находится в равновесии смесь сухого насыщенного пара и кипящей воды общей массой m = 0,05 кг. Температура внутри сосуда t = 310 ⁰С. Найдите степень сухости смеси.

Решение. Удельный объем влажного пара: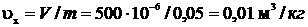

Используя [5, табл. I, с.22] определяем

t = 310 ⁰С. При этой температуре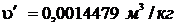

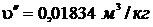
Степень сухости: 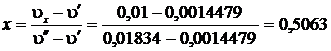или х = 50,63%

Ответ: х = 50,63%.

9.6 В барабане котельного агрегата находится кипящая вода и над ней водяной пар под давлением р = 9 МПа. Масса воды m = 5000 кг. Объем барабана V = 8 м³. Какова масса пара, находящегося над зеркалом испарения, если пар считать сухим насыщенным?

Решение. Удельный объем влажного пара: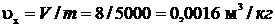

Используя [5, табл. II, с.30] определяем

р = 9 МПа = 9·10⁶ Па. При этом давлении

Степень сухости: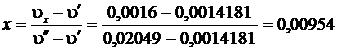

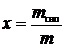, откуда масса сухого насыщенного пара: .

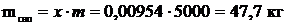Ответ: .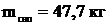

9.9 В резервуаре объемом 5 м³ находится влажный пар со степенью сухости х = 0,3. Определите массу влажного пара, объем, занимаемый водой, и объем, занимаемый сухим насыщенным паром. Давление в резервуаре р = 19,0 МПа.

Решение. Масса влажного пара: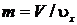

Удельный объем влажного пара: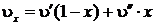

Используя [5, табл. II, с.31] определяем

р = 19 МПа = 1,9·10⁷ Па. При этом давлении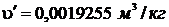

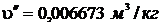
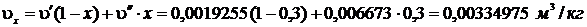
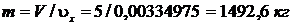
Объем, занимаемый сухим насыщенным паром: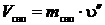

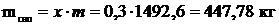
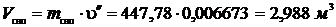
Масса воды равна: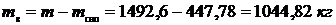

Объем, занимаемый водой: .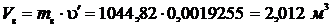

Ответ: ; ; .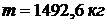

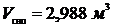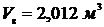9.29 К питательной воде, вводимой в прямоточный паровой котел при р = 24 МПа и t = 350 ⁰С в количестве D = 900·10³ кг/ч, от топочных газов подводится Q = 1600 ГДж/ч теплоты. Определите температуру пара на выходе из парового котла, его энтальпию и внутреннюю энергию. Падением давления при протекании воды и пара по трубам пренебречь. Представьте процесс в Т, s – и h, s – диаграммах.

Решение. Теплота, подводимая от топочных газов 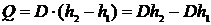, откуда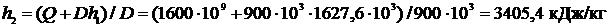

h₁ определяли по [5, табл. III, с.67] при р = 24 МПа и t = 350 ⁰С.

Значение энтальпии 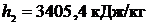находится между значениями 3382,3 кДж/кг и 3413,2 кДж/кг [5, табл. III, с.68], что соответствует температурам 560 ⁰С и 570 ⁰С. Значит, искомая температура t₂ находится в пределах от 560 ⁰С до 570 ⁰С. Проинтерполируем:

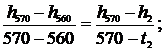
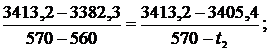откуда t₂ = 567,48 ⁰C.

;

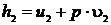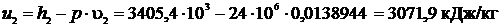
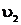определяли по [5, табл. III, с.68] при р = 24 МПа и t₂ = 567,48 ⁰С.

Ответ: 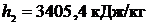; t₂ = 567,48 ⁰C; .

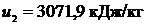9.40Водяной пар, имеющий параметры р₁ = 3,4 МПа и х₁ = 98%, изоэнтропно сжимается до р₂ = 9,0 МПа. Найдите температуру и энтальпию пара в конечном состоянии. Определите работу сжатия и изменение внутренней энергии 1 кг пара. Задачу решите, пользуясь таблицами. Проверьте результат по h, s – диаграмме.

Решение. 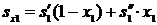, кДж/(кг·К)

Используя [5, табл. II, с.28] определяем

р₁ = 3,4 МПа = 3,4·10⁶ Па. При этом давлении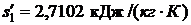

.

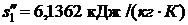
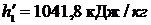
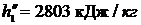
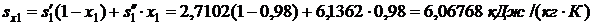Т.к. водяной пар сжимается изоэнтропно, то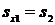

Используя [5, табл. III, с.57] определяем, что наше значение 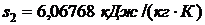находится между значениями 6,0378 кДж/(кг·К) и 6,0940 кДж/(кг·К) [5, табл. III, с.57], что соответствует температурам 350 ⁰С и 360 ⁰С. Значит, искомая температура t₂ находится в пределах от 350 ⁰С до 360 ⁰С. Проинтерполируем:

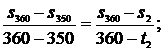
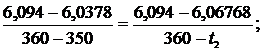откуда t₂ = 355,32 ⁰C. Аналогично для энтальпии

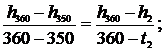
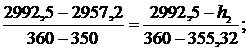откуда h₂ = 2975,98 кДж/кг

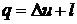, т.к. процесс – адиабатный, т.е протекающий без теплообмена с окружающей средой, то 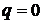, а

.

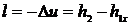
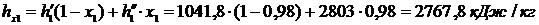
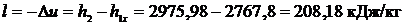Ответ: t₂ = 355,32 ⁰C; h₂ = 2975,98 кДж/кг; .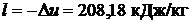

9.41 Покрытый тепловой изоляцией резервуар объемом V = 10 м³ наполовину заполнен водой при температуре насыщения и наполовину сухим насыщенным паром. Давление в резервуаре р₁ = 9,0 МПа. Быстро открывая задвижку (рис. 9.9), выпускают пар в атмосферу до тех пор, пока давление в резервуаре р₂ не становится равным 6,0 МПа, после чего задвижку закрывают. Сколько килограммов пара выпускается в атмосферу? Какой объем будет занимать пар, оставшийся в барабане после закрытия задвижки? Процесс изменения состояния Н₂О в резервуаре считать изоэнтропным.

Решение. Т.к. резервуар объемом V = 10 м³ наполовину заполнен водой при температуре насыщения и наполовину сухим насыщенным паром, то V_снп = 5 м³ и V_ж = 5 м³.

Масса сухого насыщенного пара: ,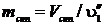

масса жидкости: .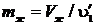

Используя [5, табл. II, с.30] определяем

р₁ = 9 МПа = 9·10⁶ Па. При этом давлении ;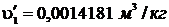

;

;

.

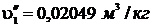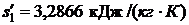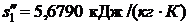Тогда ,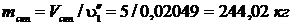

.

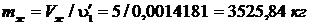Масса влажного пара до открытия задвижки: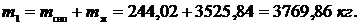

Степень сухости: .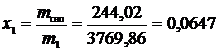

Энтропия влажного пара до открытия задвижки: .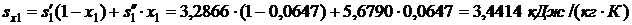

По условию задачи процесс изменения состояния Н₂О в резервуаре считать изоэнтропным, то .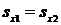

Используя [5, табл. II, с.29] определяем

р₂ = 6 МПа = 6·10⁶ Па. При этом давлении ;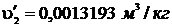

;

;

.

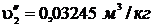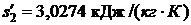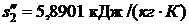Энтропия влажного пара после закрытия задвижки: 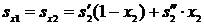, тогда

.

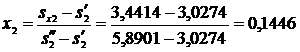Удельный объем влажного пара после закрытия задвижки: 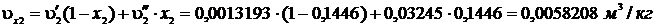Масса влажного пара после закрытия задвижки: .

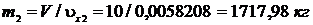Масса пара, выпущенного в атмосферу: .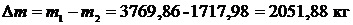

Объем, который будет занимать пар, оставшийся в барабане после закрытия задвижки: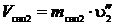

Масса сухого насыщенного пара после закрытия задвижки: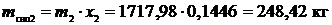

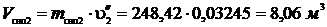
Ответ: ; .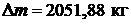

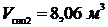Решение.

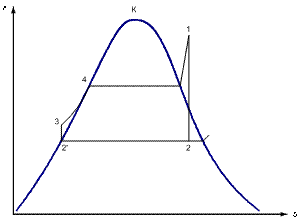
Термический КПД цикла Ренкина:

,

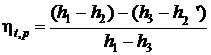где h₁ – энтальпия пара перед турбиной;

h₂ – энтальпия пара на входе в конденсатор;

h₂^’ – энтальпия воды на выходе из конденсатора;

h₃ – энтальпия воды после насоса (энтальпия питательной воды).

Термический КПД цикла Карно:

,

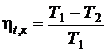где Т₁ – температура теплоисточника;

Т₂ – температура холодного источника.

Используя [5, табл. III, с.58] определяем при р₁ = 10 МПа и температуре t₁ = 530 ⁰С, что h₁ = 3451,7 кДж/кг, s₁ = 6,6965 кДж/(кг·К).

s₁ = s₂

Используя [5, табл. II, с.24] определяем

р₂ = 40 гПа = 4·10³ Па. При этом давлении ;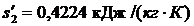

;

;

.

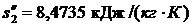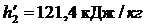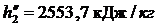t₂ = 28,96 ⁰C.

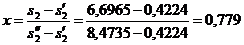
Энтальпия пара на входе в конденсатор:

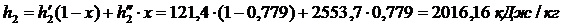
Энтальпия воды на выходе из конденсатора: 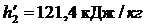и энтропия .

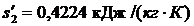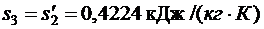
Используя [5, табл. III, с.57] при р₁ = 10 МПа определяем, что наше значение 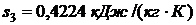находится между значениями 0,2944 кДж/(кг·К) и 0,4337 кДж/(кг·К) [5, табл. III, с.57], что соответствует температурам 20 ⁰С и 30 ⁰С. Значит, искомая температура t₃ находится в пределах от 20 ⁰С до 30 ⁰С. Проинтерполируем:

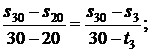
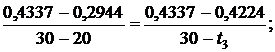откуда t₃ = 29,19 ⁰C.

Тогда для энтальпии

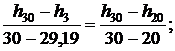
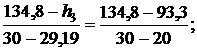откуда h₃ = 131,44 кДж/кг

Термический КПД цикла Ренкина:

.

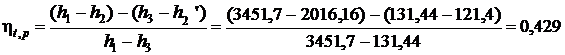Термический КПД цикла Карно:

.

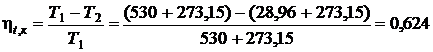Ответ: ; .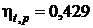

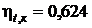14.6 При одинаковой начальной температуре t₁ = 500 ⁰C постройте кривую зависимости 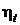цикла паротурбинной установки от начального давления р₁, приняв его равным 5,0; 10,0; 15,0 и 20,0 МПа. Давление в конденсаторе одинаково, р₂ = 40 гПа. Учтите работу питательного насоса. Представьте циклы в T,s – диаграмме.

Решение.

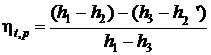
1) Используя [5, табл. III, с.54] определяем при р₁ = 5 МПа и температуре t₁ = 500 ⁰С, что h₁ = 3434,5 кДж/кг, s₁ = 6,9778 кДж/(кг·К).

s₁ = s₂

Используя [5, табл. II, с.24] определяем

р₂ = 40 гПа = 4·10³ Па. При этом давлении ;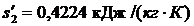

;

;

.

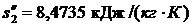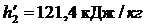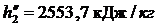t₂ = 28,96 ⁰C.

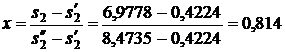
Энтальпия пара на входе в конденсатор:

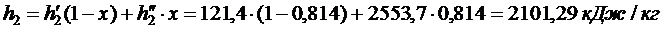Энтальпия воды на выходе из конденсатора: 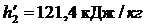и энтропия .

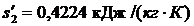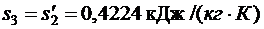
Используя [5, табл. III, с.53] при р₁ = 5 МПа определяем, что наше значение 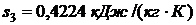находится между значениями 0,2955 кДж/(кг·К) и 0,4353 кДж/(кг·К) [5, табл. III, с.53], что соответствует температурам 20 ⁰С и 30 ⁰С. Значит, искомая температура t₃ находится в пределах от 20 ⁰С до 30 ⁰С. Проинтерполируем:

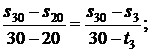
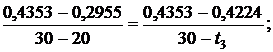откуда t₃ = 29,08 ⁰C.

Тогда для энтальпии

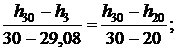
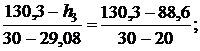откуда h₃ = 126,46 кДж/кг

Термический КПД цикла Ренкина:

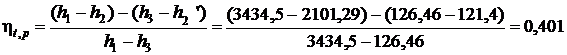
2) Используя [5, табл. III, с.58] определяем при р₁ = 10 МПа и температуре t₁ = 500 ⁰С, что h₁ = 3375,1 кДж/кг, s₁ = 6,5993 кДж/(кг·К).

s₁ = s₂

Используя [5, табл. II, с.24] определяем

р₂ = 40 гПа = 4·10³ Па. При этом давлении ;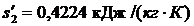

;

;

.

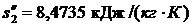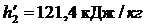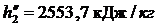t₂ = 28,96 ⁰C.

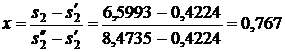
Энтальпия пара на входе в конденсатор:

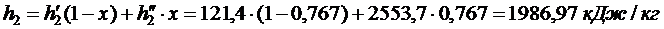Энтальпия воды на выходе из конденсатора: 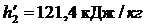и энтропия .

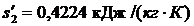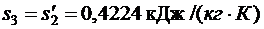
Используя [5, табл. III, с.57] при р₁ = 10 МПа определяем, что наше значение 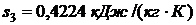находится между значениями 0,2944 кДж/(кг·К) и 0,4337 кДж/(кг·К) [5, табл. III, с.57], что соответствует температурам 20 ⁰С и 30 ⁰С. Значит, искомая температура t₃ находится в пределах от 20 ⁰С до 30 ⁰С. Проинтерполируем:

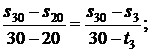
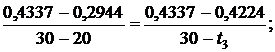откуда t₃ = 29,19 ⁰C.

Тогда для энтальпии

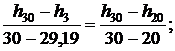
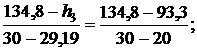откуда h₃ = 131,44 кДж/кг

Термический КПД цикла Ренкина:

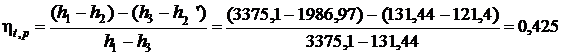
3) Используя [5, табл. III, с.64] определяем при р₁ = 15 МПа и температуре t₁ = 500 ⁰С, что h₁ = 3310,8 кДж/кг, s₁ = 6,3479 кДж/(кг·К).

s₁ = s₂

Используя [5, табл. II, с.24] определяем

р₂ = 40 гПа = 4·10³ Па. При этом давлении ;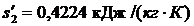

;

;

.

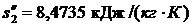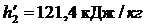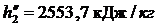t₂ = 28,96 ⁰C.

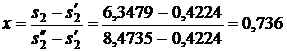
Энтальпия пара на входе в конденсатор:

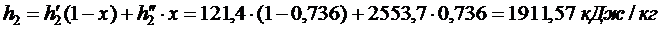Энтальпия воды на выходе из конденсатора: 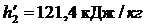и энтропия .

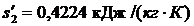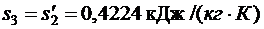
Используя [5, табл. III, с.63] при р₁ = 15 МПа определяем, что наше значение 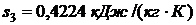находится между значениями 0,2932 кДж/(кг·К) и 0,4322 кДж/(кг·К) [5, табл. III, с.63], что соответствует температурам 20 ⁰С и 30 ⁰С. Значит, искомая температура t₃ находится в пределах от 20 ⁰С до 30 ⁰С. Проинтерполируем:

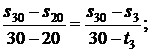
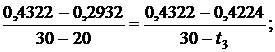откуда t₃ = 29,29 ⁰C.

Тогда для энтальпии

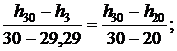
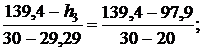откуда h₃ = 136,45 кДж/кг

Термический КПД цикла Ренкина:

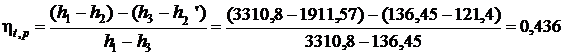
4) Используя [5, табл. III, с.66] определяем при р₁ = 20 МПа и температуре t₁ = 500 ⁰С, что h₁ = 3241,2 кДж/кг, s₁ = 6,1445 кДж/(кг·К).

s₁ = s₂

Используя [5, табл. II, с.24] определяем

р₂ = 40 гПа = 4·10³ Па. При этом давлении ;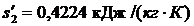

;

;

.

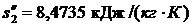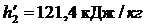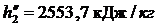t₂ = 28,96 ⁰C.

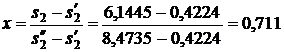
Энтальпия пара на входе в конденсатор:

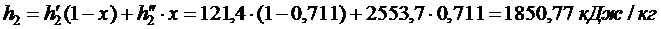Энтальпия воды на выходе из конденсатора: 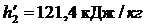и энтропия .

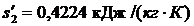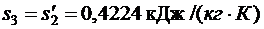
Используя [5, табл. III, с.65] при р₁ = 20 МПа определяем, что наше значение 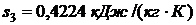находится между значениями 0,2921 кДж/(кг·К) и 0,4306 кДж/(кг·К) [5, табл. III, с.65], что соответствует температурам 20 ⁰С и 30 ⁰С. Значит, искомая температура t₃ находится в пределах от 20 ⁰С до 30 ⁰С. Проинтерполируем:

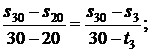
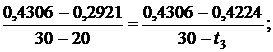откуда t₃ = 29,41 ⁰C.

Тогда для энтальпии

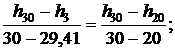
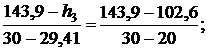откуда h₃ = 141,46 кДж/кг

Термический КПД цикла Ренкина:

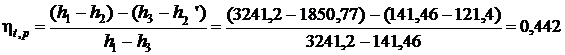
Ответ: р₁, МПа 5 10 15 20

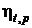0,401 0,425 0,436 0,442

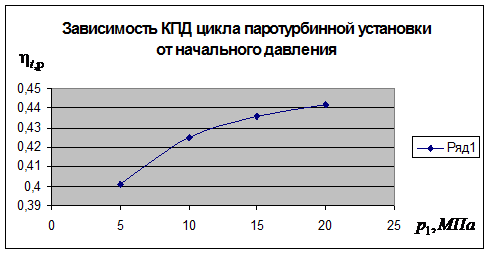
15.1 Воздушная холодильная машина должна обеспечить температуру в охлаждаемом помещении t_охл = 5 ⁰C при температуре окружающей среды t_о.с. = 20 ⁰C. Холодопроизводительность машины 840 МДж/ч. Давление воздуха на выходе из компрессора р₂ = 0,5 МПа, давление в холодильной камере р₁ = 0,1 МПа. Определите мощность двигателя для привода машины, расход воздуха, холодильный коэффициент и количество теплоты, передаваемое окружающей среде. Подсчитайте холодильный коэффициент машины, работающей по циклу Карно в том же интервале температур. Представьте цикл в T,s – диаграмме.

Решение. Холодильный коэффициент: .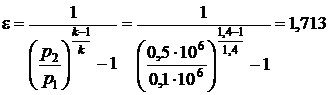

Мощность двигателя для привода машины: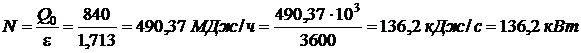

Холодильный коэффициент машины, работающей по циклу Карно: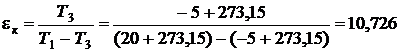

Количество теплоты, передаваемое окружающей среде: 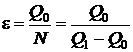, откуда .

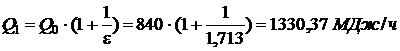Удельная холодопроизводительность: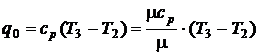

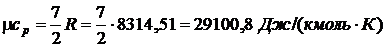[3, с.36]

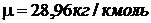
Из соотношения 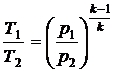находим .

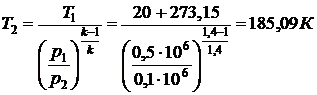Тогда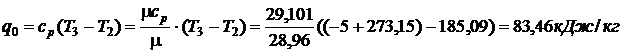

Расход воздуха: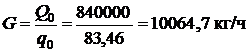

Ответ: ; ; ; ; .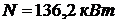

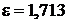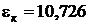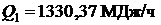15.8 Компрессор аммиачной холодильной установки имеет теоретическую мощность 40 кВт. Из компрессора сухой насыщенный пар аммиака при температуре t₂ = 25 ⁰C направляется в конденсатор, после которого жидкость в дроссельном вентеле расширяется. Температура испарения аммиака в охлаждаемой среде t₁ = -10 ⁰C. Определите холодопроизводительность установки, используя табл. 24 приложения [3].

Решение. Холодопроизводительность установки: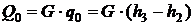

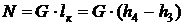, откуда 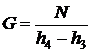, тогда

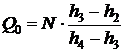
Процесс 1-2 – дросселирование ( )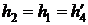

Процесс 3-4 – адиабатное сжатие ( )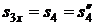

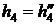находим по таблице 24 при t = 25 ⁰C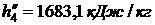

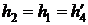находим по таблице 24 при t = 25 ⁰C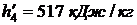

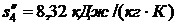определяли по таблице 24 при t = 25 ⁰C

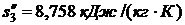определяли по таблице 24 при t = -10 ⁰C

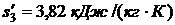определяли по таблице 24 при t = -10 ⁰C

Степень сухости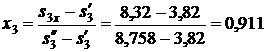

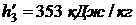определяли по таблице 24 при t = -10 ⁰C

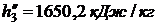определяли по таблице 24 при t = -10 ⁰C

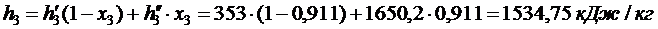
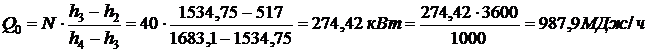Ответ: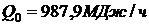

15.13 Современные электрогенераторы работают с применением водородного охлаждения. Циркулирующий в системе водород может быть использован как рабочее вещество в схеме теплового насоса (рис. 15.6). Каков отопительный коэффициент 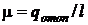этой установки, если давление водорода в системе охлаждения генератора постоянно: р₁ = р₄ = 0,097 МПа, а температура в точках 1,3 и 4 указана на схеме.

Каково давление водорода р₂ поступающего в теплообменник. Теплоемкость с_р водорода считать не зависящей от температуры.

Решение. Отопительный коэффициент .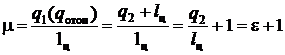

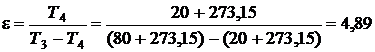. Тогда .

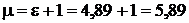Подставив значения в формулу 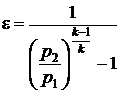, получим 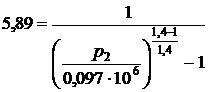откуда р₂ = 186041 Па = 0,186 МПа.

Ответ: 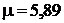; р₂ = 0,186 МПа.

б) Теплопередача [4]

Решение.

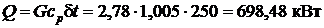
1) для цилиндрической стенки

Коэффициент теплопередачи

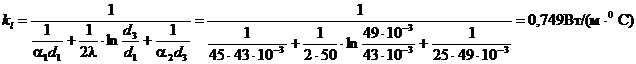
Поверхность нагрева подогревателя: 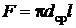, м² (1)

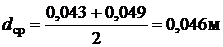
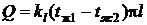(2)

Выразив из формулы (2) 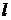и подставив в уравнение (1), получим

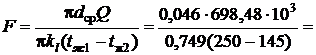
Параметры состояния. Законы и уравнения состояния идеальных газов.

1.4; 3.11; 3.15; 3.22; 3.23.

1.4 В машинном зале электростанции работают три турбины, в конденсаторах которых поддерживается абсолютное давление p₁ = 2,94 кПа, р₂ = 3,923 кН/м² и р₃ = 0,711 lbf/in². Определите величины вакуумов в процентах барометрического давления. Показание барометра в машинном зале В = 753 мм рт. ст.

Решение. Давление:

,

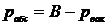где 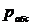- абсолютное давление;

В – барометрическое (атмосферное) давление;

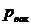- давление разряжения (вакуум).

Тогда 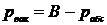. Выражаем все в Па (таблица 5, с. 291, [3]).

1) p₁ = 2,94 кПа = 2940 Па; ; ;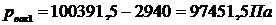

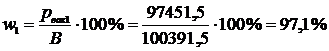2) р₂ = 3,923 кН/м² = 3,923 кПа = 3923 Па; ;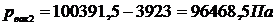

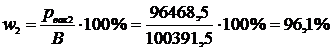
3) 10 lbf/in² = 0,68948·10⁵ Па

0,711 lbf/in² = р₃. р₃ = 4902,2 Па. ;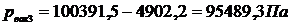

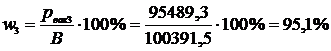
4) 10³ мм рт. ст. = 1,33322·10⁵ Па

753 мм рт. ст. = В. В = 100391,5 Па.

Ответ: , , .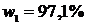

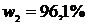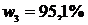3.11 Определите массу воздуха, находящегося в комнате площадью 25 м² и высотой 3,2 м. Принять, что температура воздуха в комнате t = 22⁰С, а барометрическое давление В = 986,5 гПа.

Решение.Уравнение состояния идеальных газов 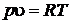, для произвольной массы газа m, кг:

,

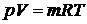где р – абсолютное давление, Па;

V – объем, м³;

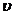- удельный объем, м³/кг;

Т – температура, К;

R – удельная газовая постоянная, Дж/(кг·К).

,

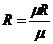где 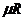- универсальная газовая постоянная, Дж/(кмоль·К).

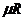= 8314,51 Дж/(кмоль·К)

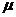- молекулярная масса, кг/ кмоль (таблица 7, с. 292, [3])

Газовая постоянная 1 кг газа R = 8314,51/ .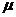

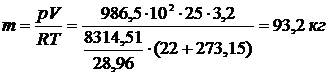
Ответ: 93,2 кг.

3.15 В комнате площадью 35 м² и высотой 3,1 м воздух находится при t = 23⁰C и барометрическом давлении В = 973 гПа. Какое количество воздуха проникнет с улицы в комнату, если барометрическое давление увеличится до В = 1013 гПа. Температура воздуха остается постоянной.

Решение.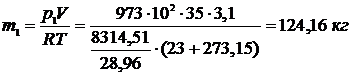

.

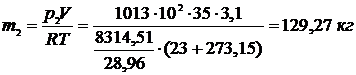
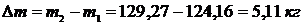Ответ :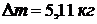

3.22 При температуре t = 800⁰C и давлении р = 0,1 МПа плотность газа 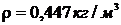. Что это за газ?

Решение. 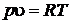, 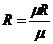→ 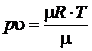, 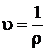.Откуда 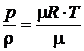. Следовательно,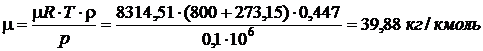

По таблице 7, с. 292 [3] определяем по молекулярной массе, что искомый газ – аргон.

Ответ:аргон.

3.23 Компрессор подает кислород в резервную емкость 3 м 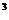. Избыточное давление в резервуаре увеличивается при этом от 0,01 до 0,6 МПа, а температура газа – от 15 до 30 ⁰С. Определите массу поданного компрессором кислорода. Барометрическое давление 993гПа.- гекто

Решение.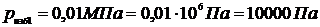

,

,

=

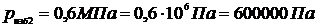
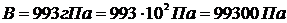
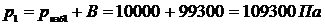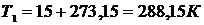
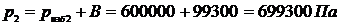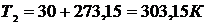
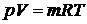
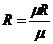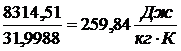
Изначальное количество кислорода, кг, в резервуаре:

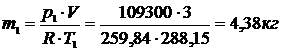
После подачи кислорода компрессором, кг:

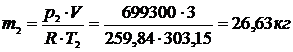
Масса поданного компрессором кислорода:

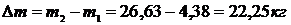
Ответ: 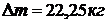.