Статистические и динамические закономерности в природе
Согласно общепринятой в физике терминологии под динамической закономерностью (или теорией) понимается закономерность, в которой связи всех физических величин однозначны. В статистических закономерностях (или теориях) однозначно связаны только вероятности обнаружения определённых значений тех или иных физических величин; связи между самими физическими величинами неоднозначны.
Для всех фундаментальных физических теорий, как динамических, так и статистических используются понятия объектов и их окружения, а также взаимодействия объектов и воздействия на объект со стороны окружения. Контролируемость взаимодействий и воздействий и определяет динамическую закономерность (или теорию), придавая связям всех физических величин однозначность.
Если же реализовать контролируемость взаимодействий и воздействий не удаётся, то реализуются статистические закономерности (или теории), в которых однозначно связаны только вероятности обнаружения тех или иных физических величин.
В процессе измерения физических величин обычно также проявляются возмущающие воздействия, задавая случайные погрешности и статистические закономерности измерений. Приведем высказывание Л.Бриллюэна, хорошо показывающее суть дела: «Законы классической механики представляют собой математическую идеализацию, которую нельзя считать соответствующей реальным законам природы…Классическая точка зрения пренебрегала действительной ролью экспериментальной погрешности. Ошибки считались случайностью. Отсюда всегда представлялось, что их можно сделать сколь угодно малыми и в конце концов ими пренебречь. Эта упрощенная картина привела к предположению о полном детерминизме в классической механике. Мы сейчас должны ясно представлять себе, что экспериментальные ошибки неизбежны, обнаружение чего делает строгий детерминизм невозможным. Ошибки - существенная черта картины мира, подлежащая учету в теории. Детерминизм необходимо заменить статистическими вероятностями». (см.: Бриллюэн Л. Научная неопределенность и информация.- М.: Мир, 1966).
Итак, динамические законы представляют собой первый, опирающийся на классическую стратегию естественнонаучного мышления, этап в процессе познания окружающего нас мира; статистические законы более совершенно отображают объективные связи в природе: они являются следующим, опирающимся на неклассическую стратегию естественнонаучного мышления, более высоким этапом познания.
Взаимодействие динамических и статистических закономерностей мы рассмотрим на примере равновесного теплового макросостояния, которое позволяет перебросить мостик к неклассическому естествознанию макромира.
Между макрообъектом (термодинамической системой) и внешним окружением (термостатом) возникают определенные виды контактов, каждому из которых соответствует конкретное условие теплового равновесия (см. схему 27).
Схема 27 . Условия теплового равновесия макросостояния.
| Виды контактов между макрообъектом и термостатом | ||
| Корпускулярный (диффузионный) контакт | Механический контакт | Тепловой (энергетический) контакт |
| Условия теплового равновесия | ||
Равенство химических потенциалов 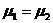 , где , где 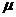 характеризует энергию передаваемую одной частицей в условиях диффузионного взаимопроникновения частиц характеризует энергию передаваемую одной частицей в условиях диффузионного взаимопроникновения частиц | Равенство давлений: P1=P2, так как работа определяется формулой А= 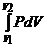 | Равенство температур: Tобъекта=Тприбора=Ттермостата |
Важно отметить, что все макроскопические параметры, характеризующие условия теплового равновесия макросостояния являются статистическими величинами и флуктуируют в условиях неконтролируемого воздействия термостата на макрообъект. В рамках равновесной термодинамики пренебрегают флуктуациями макроскопических параметров и основные законы (начала) термодинамики рассматривают, как динамические закономерности.
Схема 28. Основные законы (начала) равновесной термодинамики макросостояния.
| 1.Нулевое начало термодинамики | Если два макрообъекта А и В находятся порознь в термодинамическом равновесии с макрообъектом С и термостатом, то они находятся в термодинамическом равновесии друг с другом. Мерой термодинамического равновесия (теплового контакта) является температура. |
| 2.Первое начало термодинамики | При равновесном переходе системы между двумя макросостояниями изменение внутренней энергии не зависит от вида процесса, посредством которого произведен этот переход: 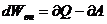 |
| 3.Второе начало термодинамики | Во всех изолированных (закрытых) системах энтропия никогда не убывает, она либо остается постоянной, либо возрастает: 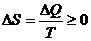 |
| 4.Третье начало термодинамики | При стремлении температуры макрообъекта к нулю его энтропия также стремится к нулю независимо от значений внешних параметров: 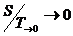 |
Формулы первого и второго начал термодинамики можно в случае равновесных макропроцессов объединить в одну формулу:

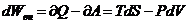 .
.
Обратим внимание, что повышение температуры в термодинамической системе можно достичь, не увеличивая ее внутренней энергии, а только за счет уменьшения энтропии.
Таким образом, оказывается пренебречь статистическими закономерностями мы можем только, если не будем учитывать не только статистический смысл макропараметров и статистический характер измерений, но также не учитывать взаимопроникновение порядка и хаоса.
Оказывается, что энтропия макросостояния пропорциональна числу микросостояний, с помощью которых реализуется данное макросостояние (термодинамической вероятности или статистическому весу макросостояния). Природа стремится к переходу от менее вероятных к более вероятным макросостояниям. Энтропия выступает в качестве меры беспорядка (хаоса): 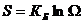 (формула Л.Больцмана).
(формула Л.Больцмана).
Принцип возрастания энтропии в изолированных (закрытых) системах свидетельствует о переходе энергии упорядоченных форм энергии в неупорядоченные в случае изолированных (закрытых) систем.
Таким образом, уменьшение энтропии возможно только в открытых системах за счет создания в них упорядоченных, например, конвективных форм движения.
В случае открытых систем (неизолированных макрообъектов) возможно, как показал И.Пригожин в рамках неравновесной термодинамики, как возрастание, так и убывание энтропии и даже ее сохранение: 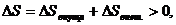 или =0, или <0.
или =0, или <0.
Фактически с понятием открытой термодинамической системы мы сталкиваемся при так называемом обогреве помещений за счет конвективного движения молекул воздуха от батареи центрального отопления вверх и обратно вниз.
Моделью хаоса является так называемое броуновское движение. Его совершают малые по массе и размеру, но все же макроскопические объекты, помещенные в некоторую среду, например жидкость или газ, находящуюся в тепловом равновесии. Если в эту макросистему, содержащую N молекул, извне попадает пылинка размером около 10-4…10-5 см, состоящая из большого числа 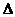 N<<N молекул, то она будет испытывать как целое столкновение с молекулами жидкости или газа. Поскольку эти молекулы движутся хаотически, их результирующее воздействие на броуновскую частицу, казалось бы, в данный момент времени должно быть в среднем равно нулю, так что броуновская частица должна была бы двигаться как свободная. Однако, на самом деле это не так. Это следует из того, что броуновская частица движется беспорядочно, постоянно изменяя направление своего движения, что можно объяснить только неравномерностью воздействия на нее молекул среды. В результате броуновская частица «чувствует» отклонения воздействия от среднего нулевого значения, которые приводят к тому, что передаваемый ей импульс всё время меняет величину и направление, а потому она движется хаотически.
N<<N молекул, то она будет испытывать как целое столкновение с молекулами жидкости или газа. Поскольку эти молекулы движутся хаотически, их результирующее воздействие на броуновскую частицу, казалось бы, в данный момент времени должно быть в среднем равно нулю, так что броуновская частица должна была бы двигаться как свободная. Однако, на самом деле это не так. Это следует из того, что броуновская частица движется беспорядочно, постоянно изменяя направление своего движения, что можно объяснить только неравномерностью воздействия на нее молекул среды. В результате броуновская частица «чувствует» отклонения воздействия от среднего нулевого значения, которые приводят к тому, что передаваемый ей импульс всё время меняет величину и направление, а потому она движется хаотически.
Как показал А.Эйнштейн, средний радиус «миграции» броуновской частицы пропорционален корню квадратному из времени «миграции»: <∆r>~D 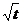 .
.
Спустя достаточно большой промежуток времени, называемый временем релаксации к тепловому равновесию, кинетическая энергия броуновской частицы приближается к предельному значению, определяемому только одним фундаментальным макропараметром – температурой среды Т, характеризующей ее свойства в тепловом равновесии. При этом среднее значение кинетической энергии в пределе не зависит от её начальной скорости. Иными словами, броуновская частица, первоначально подчинявшаяся законам классической динамики, попав в среду, в конце концов «забывает» о своих характеристиках и начальных данных. В результате столкновений с молекулами среды она «запутывается» в макросистеме и становится её неотъемлемой частью.
Аналогичный процесс приближения к тепловому равновесию происходит в любой макросистеме, при этом в роли броуновской частицы может выступать не только «инородный» макроскопический объект, но и любая молекула, например, идеального газа.
Как мы уже отмечали, фундаментальным параметром – мерой теплового равновесия является температура.
Итак, даже начала равновесной термодинамики можно только приближённо считать динамическими законами. При учёте соотношения неопределенностей А. Эйнштейна:
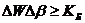 , где
, где 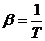 , или
, или 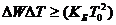 ,
,
где Т0-температура термостата, более оправдано говорить о статистической термодинамике, в которой важнейшей проблемой является, как выразить макропараметры через известные характеристики микрообъектов. Эту проблему, хотя и частично, решил знаменитый американский физик Дж. Гиббс. Ему удалось показать, что в условиях теплового равновесия микрообъекты, составляющие макрообъект, находятся в специфическом микросостоянии, которое описывается распределением микрочастиц по группам с определенной энергией:
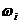

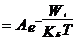 ,
, 
где 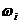 – вероятность нахождения частиц в группе с энергией
– вероятность нахождения частиц в группе с энергией 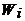 . Распределение Гиббса записывается в квазиклассическом виде и фиксирует зависимость соответствующего микросостояния от абсолютной температуры термостата T, а в более общем микроканоническом виде – от химического потенциала μ и давления P.
. Распределение Гиббса записывается в квазиклассическом виде и фиксирует зависимость соответствующего микросостояния от абсолютной температуры термостата T, а в более общем микроканоническом виде – от химического потенциала μ и давления P.
Распределение Гиббса взаимосвязано с таким фундаментальным макропараметром, как энтропия. Можно сказать, что фактически энтропия является макроскопическим «образом» распределения Гиббса.
Напомним, что микросостояние типа волновой функции формируется макрообстановкой (окружением микрообъекта), в которую включается и система «человек + прибор». Эти микросостояния оказываются весьма разнообразными. Распределение Гиббса в качестве микросостояния оказывается проще, поскольку в нём роль универсальной макрообстановки выполняет только термостат. Так, например, в случае идеального газа (совокупности классических микрочастиц) квазиклассическое распределение Гиббса можно выразить в виде обобщённого статистического распределения Больцмана-Максвелла:
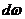 =
= 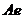
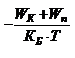
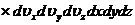 .
.
Квазиклассичность соответствующей формулы связана с тем, что нельзя одновременно точно, исходя из соотношения неопределенностей Гейзенберга, измерить координату и проекцию скорости микрочастицы.
Из обобщённого статистического распределения Больцмана-Максвелла можно вывести распределение Максвелла молекул идеального газа по абсолютным их скоростям.
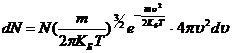 , графически изображённого на схеме (слева).
, графически изображённого на схеме (слева).
Схема 29. Статистические распределения
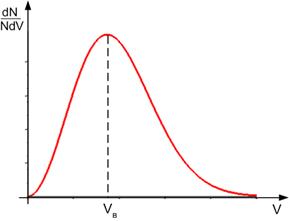 | 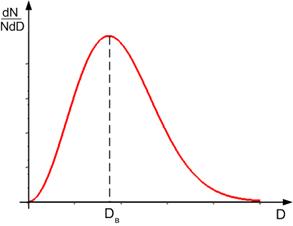 |
На той же схеме справа приведено распределение людей по абсолютным их доходам. Нетрудно заметить определённое сходство этих распределений, т.е. статистические распределения (закономерности) играют важную роль во всех сегментах интеллектуальной сферы культуры.
Из обобщённого распределения Больцмана-Максвелла также можно вывести распределение Больцмана молекул идеального газа по высоте в однородном поле тяжести, а также барометрическую формулу изменения давления воздуха атмосферы с высотой:
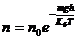 и
и 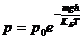 .
.
В случае относительного постоянства температуры в нижних слоях тропосферы барометрическую формулу используют для определения высоты в низколетящих вертолётах и самолётах.
Квантовые статистики используют, как мы уже отмечали, принцип тождественности квантовых частиц, имеющих одинаковые массы, заряды и спины (внутренние характеристики микрочастиц), что позволяет разделить мир элементарных частиц на бозоны (коллективисты) и фермионы (индивидуалисты).
В постнеклассической стратегии естественнонаучного мышления теории взаимодействия порядка и хаоса становятся определяющими в теориях наук о сложных системах: экологии (Э.Геккель(1834-1919)), кибернетики и теории информации (Н.Винер(1894-1964)), синергетики (Г.Хакен(р.1927)), неравновесной термодинамики (И.Пригожин(р.1917)), нелинейной динамики.
Физика Вселенной
Физика Вселенной изучается космологией – астрофизической теорией структуры и динамики изменения Метагалактики, включающей в себя и определенное понимание свойств всей Вселенной. Выделяют также астрофизику, включая в нее не только космологическую, но и космогоническую науку о структуре и динамике изменения нашей солнечно-планетной системы. Очень часто астрофизические космологические и космогонические теории объединяют в единое понятие физики Мегамира.
Схема 30. Мегамир.

Фрактальная структура стрел времени опирается на принцип глобального эволюционизма, ярко выраженного в основной идее астрофизики: «Звезды рождаются, живут и умирают, как и всё в этом мире». Для обоснования концепции стрел времени важную роль играет энтропия Вселенной – её количественная оценка и характер распределения между основными материальными объектами. Соответствующие оценки, проведенные для Вселенной, показывают, что основным носителем энтропии Вселенной, играющим тем самым роль её «термостата», является реликтовое фоновое космическое излучение, состоящее из безмассовых частиц (фотонов, нейтрино). Наличие массы у нейтрино носит в настоящее время в значительной степени гипотетический характер. Соответствующая энтропия составляет величину Sизл.~ 1090 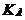 (в расчете на единицу сопутствующего веществу объема Вселенной). Заметим, что величина Sизл. практически не изменяется с очень ранних стадий эволюции Вселенной (начиная с 1 с после Большого взрыва). С другой стороны, суммарная энтропия Sизл для совокупности массивных объектов (космических тел) Вселенной ничтожна мала по сравнению с Sизл.. Наконец, оценка максимально возможной энтропии Вселенной в гипотетическом полностью равновесном состоянии «черной дыры» с той же массой составляет Sравн .~ 10124
(в расчете на единицу сопутствующего веществу объема Вселенной). Заметим, что величина Sизл. практически не изменяется с очень ранних стадий эволюции Вселенной (начиная с 1 с после Большого взрыва). С другой стороны, суммарная энтропия Sизл для совокупности массивных объектов (космических тел) Вселенной ничтожна мала по сравнению с Sизл.. Наконец, оценка максимально возможной энтропии Вселенной в гипотетическом полностью равновесном состоянии «черной дыры» с той же массой составляет Sравн .~ 10124 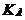 . Таким образом, принимая, что при бесконечно больших временах энтропия Вселенной стремится к своему равновесному значению, для слагаемых полной энтропии Вселенной SВс = Sизл. + Sвещ. получаем следующую цепочку неравенств:
. Таким образом, принимая, что при бесконечно больших временах энтропия Вселенной стремится к своему равновесному значению, для слагаемых полной энтропии Вселенной SВс = Sизл. + Sвещ. получаем следующую цепочку неравенств:
Sвещ. << Sизл << Sравн.
Из нее следует, по крайней мере, два важных вывода. Во-первых, эволюция во Вселенной идёт (и, по-видимому, ещё долго будет продолжаться), по существу, в характерных для изолированной системы условиях, когда
SВс = Sизл. + Sвещ. » Sизл = const. Во-вторых, окружающая нас часть Вселенной ещё очень далека от своего максимального неупорядоченного (равновесного) состояния, соответствующего полному коллапсу. Возможно, именно эта неравновесность наблюдаемой Вселенной является причиной справедливости второго начала термодинамики для всех замкнутых подсистем в ней.
Наконец в контексте неравенства Sвещ. << Sизл становится вполне понятным весьма важный феномен спонтанного возникновения «порядка из хаоса», который описан И.Р. Пригожиным. Он заключается в том, что в природе при определенных условиях становится вполне возможным процесс самоорганизации, т.е. образование компактных структур с достаточно большими флуктуациями их «внутренней» энтропии D S , при D S < 0 эти процессы сопровождаются усложнением структуры, при D S > 0 – их упрощением, деградацией, но в любом случае |D S| << Sизл . Существенно, что при D S < 0 происходит компенсация убыли энтропии в системе и её избыток в виде «внешней» энтропии (по абсолютной величине превосходящей |D S|) отдаётся термостату, так что в конечном итоге энтропия Вселенной всё-таки возрастает в полном соответствии со вторым началом термодинамики.
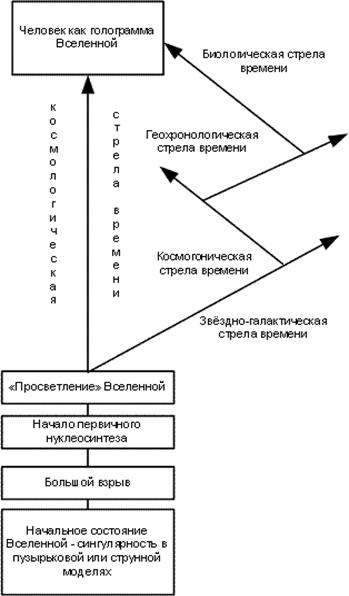
Древо эволюции в концепции стрел времени использует в качестве корневой системы стандартную теорию Большого взрыва и представлено на схеме 31.
Схема 31. Древо эволюции мира (универсума) в контексте стрел времени.
Экспериментальным подтверждением стандартной теории Большого взрыва являются:
1. Расширение Вселенной – разбегающиеся галактики (красное смещение линий в спектрах элементов удаленных галактик в сторону более длинных волн по сравнению с линиями в спектрах аналогичных элементов на Земле).
2. Реликтовое излучение фотонов и нейтрино, образовавшихся в ранней стадии расширения Вселенной.
3. Химический состав наблюдаемой части Вселенной в среднем одинаков: вещество в ней на 77% состоит из водорода и на 22% - из гелия, причем такое значительное обилие гелия невозможно объяснить термоядерными реакциями в звездах.
4. Значительное превышение концентрации фотонов космического электромагнитного излучения, не имеющего никакого отношения к излучению наблюдаемых ныне звезд и других объектов, над концентрацией вещества (барионов-протонов и нейтронов):
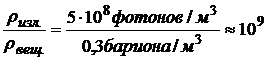
5. Оценки возраста горных пород Земли и метеоритов дают значения времени их существования 4,5…17,5 млрд. лет, что служит косвенным указанием для величины возраста Вселенной.
6. Вселенная в целом находится в состоянии, далеком от теплового равновесия, и в условиях, когда видимое вещество в ней очень разрежено.
7. Модель Галактики и Метагалактики, приведенная ниже (схема 32).
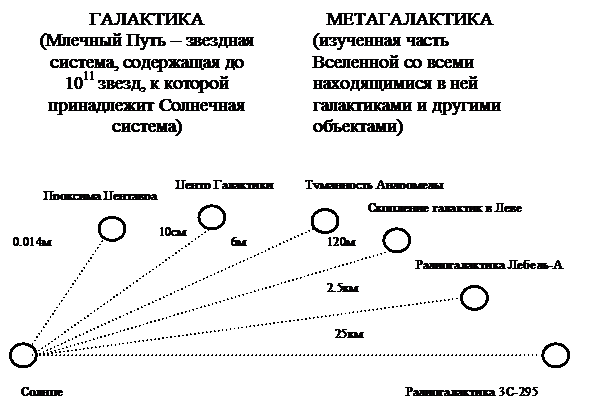 Схема 32. Модель Галактики и Метагалактики.
Схема 32. Модель Галактики и Метагалактики.
| Масштаб: Земная орбита = внутренней орбите атома водорода в классической модели Бора (радиус этой орбиты равен 0,53×10-8см) Галактика в этом масштабе: · Расстояние до ближайшей звезды Проксима будет 0,014 мм; · Расстояние до центра Галактики около 10 см; · Размеры нашей звездной системы будут около 35 см; · Диаметр Солнца будет 0,0046А (ангстрем – единица длины, равная 10-8см). Реальные размеры Галактики: диаметр – 120 тыс. световых лет, толщина 10 тыс. световых лет | Метагалактика в этом масштабе: · Расстояние до туманности Андромеды будет 6м (реальное её удаление 1,5 млн. световых лет); · Расстояние до центральной части скопления галактик в Деве, куда входит и наша местная система галактик будет 120м, причем такого же порядка будет размер самого скопления (реальное удаление 50 млн. световых лет); · Расстояние до радиогалактики Лебедь-А будет 2,5км; · Расстояние до радиогалактики 3С-295 будет 25км (реальное ее удаление 5 млрд. световых лет). Скорость удаления радиогалактики Лебедь-А – около 17 тыс. км/с, радиогалактики 3С-295 – около 138 тыс. км/с _____________________________ Реальные размеры Метагалактики около 20 млрд. световых лет |
В стандартной модели эволюции на космологическом уровне выделяют основные этапы космической шкалы времени, которые совместно с характерными процессами им соответствующими, приведены фрагментарно в схеме 33.
Схема 33 . Космическая шкала времени в стандартной космологической модели эволюции Вселенной.
| Этапы | Характерные процессы | Время от сегодняшнего момента | ||
| Название | Космическое время | Температура (К) | ||
| 1. Начальное состояние Вселенной – сингулярность | Существуют две модели сингулярности точечная (пузырьковая) и струнная. Для обеих моделей характерным является переход к стандартной модели Большого взрыва | |||
| 2. Большой взрыв | В пузырьковой модели Вселенная от первоначального сингулярного состояния перешла к расширению (около 20 млрд. лет назад). В результате Большого взрыва образовалась не только материя, но и пространство-время, задающее начало рождения Вселенной. В струнной модели задание времени рождения Вселенной оказывается сложной гипотетической задачей. Общим в обеих моделях является существование единого фундаментального взаимодействия. | 20 млрд. лет | ||
| 3. Этап первичного синтеза, включающий в себя следующие эпохи: 3.1 Планка; 3.2 Барионов; 3.3 Адронов; 3.4 Лептонов; 3.5 Синтеза ядер; 3.6 Вещества; 3.7 Прозрачной Вселенной. | 10-42с 10-35с 10-6с 10-3с 100с 104 лет 2×105 лет | 1032 1028 1014 1012 109 | Рождение элементарных частиц, во Вселенной доминирует излучение; установление числа барионов; возникновение асимметрии между материей и антиматерией; аннигиляция протоно-антипротонных пар; аннигиляция электронно-позитронных пар; становление первоначального физико-химического состава Вселенной (ядер водорода -70%, ядер гелия (a-частиц) – 30%); во Вселенной начинает доминировать вещество, состоящее из нейтральных атомов водорода, дейтерия и гелия с небольшой примесью водорода; отделение излучения от вещества. | 19,7 млрд. лет |
| 4. Этап формирования галактик, в том числе и нашей галактики, включающий в себя следующие эпохи: 4.1 Начало образования галактик; 4.2 Галактики начинают образовывать скопления; 4.3 Сжатие нашей протогалактики; 4.4 Образование звезд; 4.5 Образование межзвездного облака, давшего начало Солнечной системе; 4.6 Образование планет. | 1-2 млрд. лет 3 млрд. лет 4 млрд. лет 4,1 млрд. лет 15,2 млрд. лет 15,4 млрд. лет | 2,7 | Создание неустойчивостей относительно флуктуаций плотности за счет гравитационного взаимодействия в неравновесной смеси газов из нейтральных атомов и фотонов. Гравитационному коллапсу (полному сжатию) препятствуют вращение и внутреннее давление, причем до отделения излучения от вещества силы давления излучения превышали гравитационные. Критический размер и масса объекта, для которого обе силы (гравитации и внутреннего давления) уравновешиваются, называются длиной и массой Джинса. Если исходный размер объекта превосходит длину Джинса, должна наблюдаться его фрагментация. Если же этот размер меньше длины Джинса, то объект должен коллапсировать как целое. Образование иерархической структуры Вселенной – галактик, их скоплений, с одной стороны, и звезд, шаровых скоплений, планет и т.п., с другой – обусловлено флуктуациями плотности, имеющими различную природу. Формирование галактик сопровождалось возникновением и эволюцией звезд различных масс, в которых путем различного рода ядерных реакций создавались в разных пропорциях легкие, средние и тяжелые элементы. | 19 – 18 млрд. лет 17 млрд. лет 16 млрд. лет 15,9 млрд. лет 4,8 млрд. лет 4,6 млрд. лет |
Рассмотрим фрагментарно классификацию галактик и звезд (схема 34).
Схема 34 . Классификация галактик.
| Наименование | Тип | Масса в массах Солнца |
| Яркие сверхгигантские галактики | Эллиптические | 1013 |
| Сверхгигантские галактики | Эллиптические и спиральные | 1012 – 1011 |
| Гигантские и карликовые галактики | Эллиптические, спиральные и неправильные | 1010 – 108 |
| Карликовые галактики и пигмеи | Эллиптические | 107 – 106 |
Млечный путь входит в группу, включающую около двадцати галактик, которую называют Местной. Помимо нашей галактики в неё входит туманность Андромеды – гигантская спиральная галактика (М 31, расстояние до неё 670 килопарсек или 1,5 млн. световых лет, масса - 3×1011 масс Солнца), Малое Магелланово Облако – неправильная галактика, Большое Магелланово Облако – нечто промежуточное между спиральной и неправильной галактиками (расстояние до них соответственно 63 и 52 килопарсек, их масса соответственно 2×109 и 1×1010 масс Солнца), и ряд неправильных и эллиптических галактик. Диаметр нашей Местной группы галактик 5 млн. световых лет.
Схема 35 . Виды звезд.


Схема 36 . Эволюция звезд
(варианты развития).
 |



 I.
I.
|
|
| |||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||



 II.
II.
|
|
|
|
 | |||
 | |||
 III.
III.
 |  | ||||||||
| |||||||||
| |||||||||
| |||||||||
Варианты развития звезд:
I. Звезды массой от 1 до 1,2 массы Солнца эволюционируют к белому карлику, который, остывая, превращается в черного карлика.
II. Звезды с массой 2,0 массы Солнца эволюционируют к нейтронной звезде: последняя, если сможет захватить межзвездный газ или вещество двойной звезды, превращается в черную дыру.
III. Звезда с массой более 2,0 массы Солнца эволюционирует к черной дыре через коллапс звезды.
