Уравнение моментов или основное уравнение динамики вращательного движения

Это уравнение можно получить, умножив векторно обе части второго закона Ньютона на радиус-вектор r, определяющий положение материальной точки или ЦМ тела относительно произвольного полюса О: 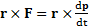. Тогда с учетом определений момента силы: 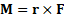и момента импульса 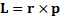, а также представления 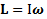и определения углового ускорения 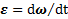придем к уравнениям динамики вращательного движения

, , .

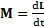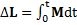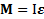Пример 1: К концам нити, перекинутой через цилиндрический блок массой M и радиусом R, привязаны два груза с одинаковой массой m. На один из грузов кладут перегрузок массой 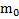. Найти ускорения грузов, силы натяжения нитей и силу давления перегрузка на тело.

Рис.62

Дано: 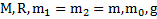. Найти: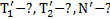

Решение:Второй закон Ньютона для каждого из тел (рис.62) в проекциях на направление их ускорения и уравнение вращательного движения блока имеют вид

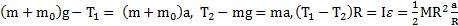или .

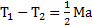Складывая эти три уравнения, получим 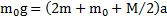. Откуда ускорение тел

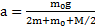. Реакции нитей 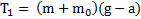, 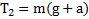. Второй закон Ньютона для перегрузка 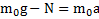. Откуда реакция тела, на которое положен перегрузок 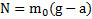. Силы натяжения нитей и силу давления перегрузка на тело находим по третьему закону Ньютона .

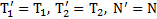Ответ: , , , .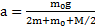

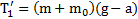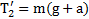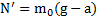Пример 2. К концам нити, перекинутой через цилиндрический блок, привязаны два груза с одинаковой массой m. В разрезы нитей вставлены динамометры. На один из грузов кладут перегрузок массой 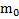. Найти массу блока и ускорение движения грузов, если отношение сил натяжения нитей по показаниям динамометров равно 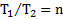, где 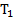– сила натяжения нити, к которой прикреплено тело с перегрузком.

Дано: 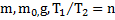. Найти: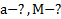

Решение: Натяжения нитей найдены в примере 1. Откуда 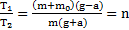и ускорение движения грузов 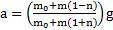. Сила натяжения первой нити 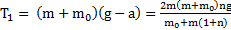, а второй .

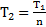Согласно примеру 1 из уравнения вращательного движения блока следует, что 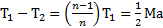. Откуда масса блока .

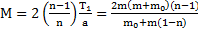Ответ: , .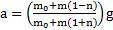

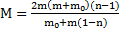Пример 3.Диск радиуса R насажен на стержень радиуса r, изготовленный из того же материала, что и диск. Массы диска и стержня равны 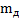и 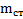. На обод диска насажено кольцо массой 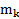и внутренним и внешним радиусами 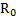и R. Вся система (маятник Максвелла) подвешена на двух нитях одинаковой длины, прикрепленных по разные стороны диска к стержню (рис.63). В результате ось маятника параллельна горизонтальной поверхности. Маятник поднимают на высоту 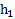, накручивая нити на стержень, и отпускают, и после рывка он поднимается на высоту 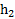. Найти ускорение движения маятника до и после рывка нитей, время его движения от начальной точки до точки максимального подъема, модуль изменения его момента импульса и изменение модуля (величины) момента импульса при рывке нити и количество теплоты, выделившееся при этом.

Рис.63

Дано: 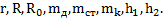Найти: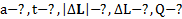

Решение: Масса маятника 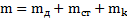. Моменты инерции диска, стержня и кольца относительно оси маятника 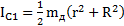, 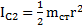и 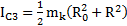. Полный момент инерции маятника относительно его оси 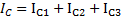. Момент инерции маятника относительно точек О касания нитей и стержня .

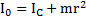До и после рывка нитей маятник движется под действием одного и того же набора сил (реакции нитей Tи его силы тяжести 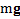), поэтому ускорение 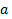его ускоренного и замедленного движения до и после рывка нитей будет одинаковым. Его можно найти, например, написав уравнение вращательного движения маятника 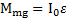относительно точек О касания нитей и стержня 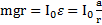. Откуда ускорение движения маятника .

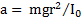Его можно также найти, используя закон сохранения энергии: 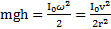. Опять получим .

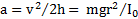Путь, проходимый маятником на любом участке его движения, дается уравнениями кинематики: 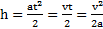. Откуда скорости маятника до и после рывка нити равны 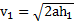и 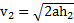. Время движения маятника до рывка нити 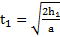, а после рывка до точки максимального подъема 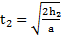, и полное время движения маятника от начала его движения до точки максимального подъема равно .

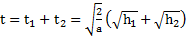Моменты импульса маятника относительно его оси до и после рывка нитей равны 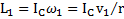и 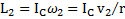. Тогда модуль изменения момента импульса маятника при рывке нитей с учетом, что после рывка нитей направление вектора его момента импульса изменяется на противоположное, равен 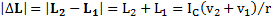. Но изменение модуля (величины) момента импульса будет равно .

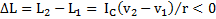Количество теплоты, выделившееся при рывке нитей, с учетом, что кинетическая энергия маятника в начальной и конечной точках его движения равна нулю 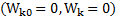, согласно закону сохранения энергии равно .

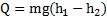Ответ: , , , , , , , , , .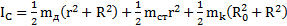

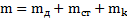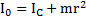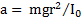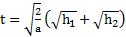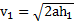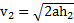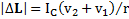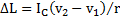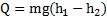Пример 4. Ось маятника Максвелла (пример 3) массой m и радиусом оси r подвешена на двух нитях одинаковой длины. Наматывая нить на ось, маятник поднимают на высоту 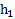и отпускают, Через время 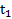происходит рывок нити и маятник поднимается на высоту 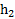. Найти ускорение движения маятника, время его движения от начальной точки до точки максимального подъема, его собственный момент инерции, модуль изменения его момента импульса и изменение модуля (величины) момента импульса при рывке нити и количество теплоты, выделившееся при этом.

Дано: 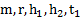.Найти: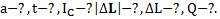

Решение: Набор уравнений, описывающий движение тела, не зависит от структуры таблицы дано-найти, изменится лишь алгоритм решения задачи.

Согласно уравнениям примера 3 ускорение движения маятника 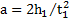. Собственный момент инерции маятника: 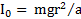, 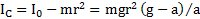. Отношения времен подъема и опускания маятника 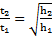. Время движения маятника от начальной точки до точки его максимального подъема 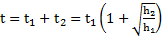. Скорости маятника перед рывком и после рывка нити – 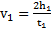и .

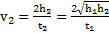Модуль изменения момента импульса маятника при рывке нитей 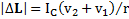. Изменение модуля (величины) момента импульса 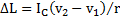. Количество теплоты, выделившееся при рывке нитей .

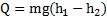Ответ: , , , , , , , .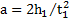

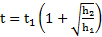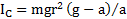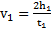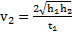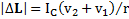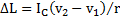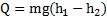Пример 5. Круглое тело массой m с коэффициентом инерции k скатывается без проскальзывания с наклонной плоскости с углом наклона α. Найти ускорение тела и силу трения, действующую на него, а также значение коэффициента трения, при котором скольжения не будет.

Рис.64

Дано: m, k, g, α. Найти: , μ –?

Решение: Возьмем полюс в точке О касания тела и плоскости (рис.64), через которую проходит мгновенная ось вращения тела (проскальзывание тела относительно плоскости отсутствует). Относительно этой точки моменты сил Nи 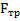равны нулю: 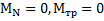, а момент силы тяжести равен 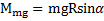. Момент инерции круглого тела относительно оси О по теореме Штейнера 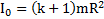, угловое ускорение вращения тела 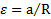. Тогда уравнение вращательного движения тела относительно оси О 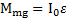примет вид 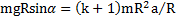. Отсюда ускорение скатывания тела .

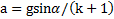Если выбрать полюс в точке С (ЦМ тела), то моменты сил N и mg относительно оси С будут равны нулю: 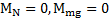, а момент силы трения будет равен 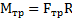. Момент инерции тела относительно оси С 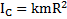, а угловое ускорение его вращения 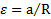.Тогда уравнение вращательного движения тела относительно оси С 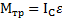примет вид 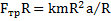. Откуда 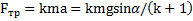. Силу трения можно также найти из второго закона Ньютона для ЦМ тела: 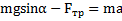. Результат будет прежним. Найденная сила трения сцепления аналогична силе трения покоя. Как известно, максимальная сила трения покоя 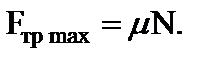В данной задаче 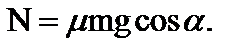Следовательно, 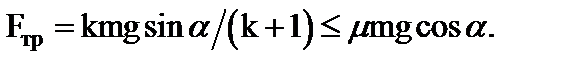Отсюда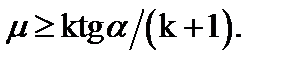

Ответ: , ,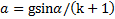

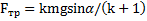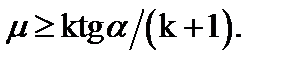
Пример 6. Два круглых тела с коэффициентами инерции 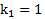(полый цилиндр) и 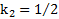(сплошной цилиндр) одинаковой массы и одинаковыми радиусами начинают скатываться без проскальзывания с наклонной плоскости высотой h и углом наклона α одновременно. Найти скорости тел в основании наклонной плоскости и времена их скатывания с нее. Во сколько раз отличаются ускорения, времена скатывания тел и их скорости в основании наклонной плоскости?

Дано: 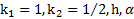. Найти: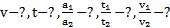

Решение: Ускорения тел найдены в примере 5. При скатывании тела проходят одинаковые пути 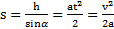. Откуда время скатывания тела 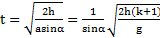, а его скорость в основании наклонной плоскости 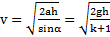. Отношения ускорений, времен и скоростей тел: , .

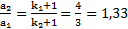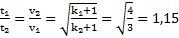Ответ: , , , .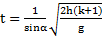

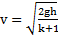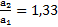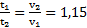Пример 7. Круглое тело с коэффициентом инерции 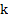скатывается с наклонной плоскости с углом наклона α без проскальзывания и оказывается в основании наклонной плоскости через время t. Найти высоту наклонной плоскости и скорость тела в ее основании.

Дано: α, k, g,t. Найти:h-?,v-?

Решение: Согласно примеру 3 ускорение скатывания тела 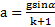. Путь, проходимый телом вдоль наклонной плоскости 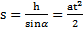. Откуда высота наклонной плоскости 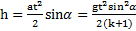, а скорость тела в ее основании .

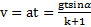Ответ: , .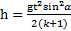

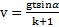Пример 8. Два круглых тела скатываются с наклонной плоскости без проскальзывания. При этом оказалось, что отношение времен их скатывания 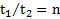. Во сколько раз отличаются ускорения скатывания тел и их скорости в основании наклонной плоскости? Чему равен коэффициент инерции второго тела, если коэффициент инерции первого тела равен ?

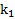Дано: 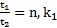.Найти: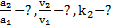

Решение: При скатывании с наклонной плоскости тела проходят одинаковые пути 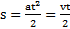. Откуда 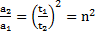, 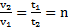. Согласно примеру 4 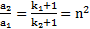, откуда .

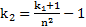Ответ: 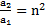, , .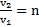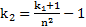