Понятие электронного облака. Его физический смысл.

Общий вид волновых функций достаточно сложен.

Рассмотрим для примера волновую функцию основного состояния электрона– 1s-состояние, т.е. состояния с минимальной энергией: n = 1, l = 0, m = 0.

Кратность вырождения n² = 1, т. е. состояние невырожденное. Так как l = 0, то М = 0, М_z = 0.

Функция Y, представляющая собой собственную функцию оператора квадрата момента импульса для s-состояния (с нулевым моментом импульса) будет постоянной. Это соответствует тому, что движение электрона не зависит от углов θ и φ и будет только радиальным, а пси-функция 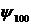( а также все пси-функции вида 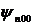) зависит только от r и будет сферически симметричной.

Решение уравнения Шредингера для s-состояния дает следующий вид пси-функции

,

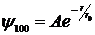где r₀ – радиус первой боровской орбиты, A – нормирующая константа.

Так как от понятия траектории пришлось отказаться, то ввели понятие «электронного облака», плотность распределения которого в каждой точке пропорциональна плотности вероятности местонахождения электрона в этой точке.

Плотность вероятности обнаружить электрон на расстоянии r будет определяться с учетом того, что элемент объема в сферической системе координат

,

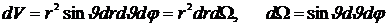где 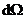- элемент телесного угла. Проинтегрировав это выражение по полному телесному углу 4π, найдем вероятность того, что электрон окажется в тонком шаровом слое между r и r + dr

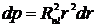
Плотность вероятности нахождения электрона на расстоянии r от ядра определяется величиной

.

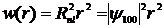Графически распределение плотности вероятности выглядит, например для состояния 1s следующим образом (рис.4).

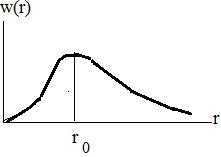
Рис.4

Плотность вероятности w(r) обращается в нуль при r = 0 и асимптотически стремиться к нулю при 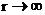. Таким образом, имеется определенная вероятность найти электрон на любом расстоянии от ядра. Мы можем определить расстояние, на котором эта вероятность будет максимальна. Полученный результат покажет, что максимум вероятности будет соответствовать расстоянию от ядра, совпадающему с величиной радиуса первой боровской орбиты r₀. Так как состояние 1s характеризуется сферической симметрией, то распределение вероятности представляет собой сферическое облако, а не плоский образ, соответствующий боровской орбите.

Пример для состояния 2s: n = 2, l = 0, m = 0 (рис.5).

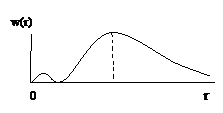
Рис.5

Пространственное квантование момента импульса имеет следующий вид (рис.6)

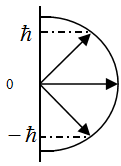
Рис.6

Угловое распределение плотности вероятности нахождения электрона в атоме водорода определяется видом угловой функции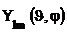

1) в s-состоянии (l = 0)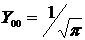

2) в p –состоянии (l = 1, m = -1, 0, +1)

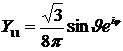
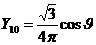
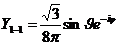(Рис.7)

Рис.7

Для получения пространственного образа надо представить себе тело вращения, возникающее путем вращения избраженных фигур вокруг соответствующих осей.

Вопросы для самоконтроля:

1. Запишите уравнение Шредингера, которому удовлетворяет состояние электрона в атоме водорода.

2. Что характеризует квантовые числа: главное n, орбитальное l и магнитное m? Какие значения они могут принимать?

3. Каковы возможные значения l и m, для главного квантового числа n=3?

4. Сколько различных состояний соответствует n=2?

5. Чему равна плотность вероятности обнаружения электрона в основном состоянии атома водорода?

6. Атом водорода может иметь одно и тоже значение энергии находясь в различных состояниях? Как они называются?

7. Каковы правила квантования орбитального и собственного моментов импульса электронов? Их проекций на направления внешнего магнитного поля?

8. Что представляет из себя электронное облако? Каков его смысл?

Лекция 8.

АТОМЫ В МАГНИТНОМ ПОЛЕ

План

1. Орбитальный механический и магнитный моменты электрона.

2. Спин электрона.

3. Опыт Штерна и Герлаха.

1.Орбитальный механический и магнитный моменты электрона.Пусть электрон движется со скоростью v по орбите радиуса r . Через площадку, расположенную в любом месте на пути электрона, за время t переносится заряд q = eνt, где e – заряд электрона, ν – число оборотов в секунду. Следовательно, движущийся по орбите электрон образует круговой ток силы

I = 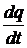= eν.

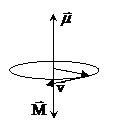Поскольку заряд электрона отрицателен, направление движения электрона и направление тока противоположны. Магнитный момент создаваемого электроном тока равен

,

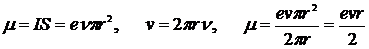где v – скорость движения электрона.

Момент обусловлен движением электрона по орбите, вследствие чего его назвали орбитальным магнитным моментом электрона. Направление вектора μобразует с направлением тока правовинтовую систему, а с направлением движения электрона – левовинтовую.

Орбитальный механический момент импульса 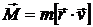образует с направлением движения электрона правовинтовую систему. Следовательно, вектора μ и М ориентированы перпендикулярно плоскости орбиты и противоположно направлены.

Отношение магнитного момента электрона к его механическому моменту называется гиромагнитным отношением. Получим

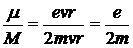
По Бору М = mvr = nћ. Следовательно,

,

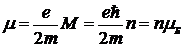где 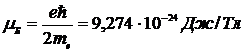- магнетон Бора.

Из решения уравнения Шредингера для атома водорода мы получили, что квантование момента импульса по величине отличается от квантования его по Бору и определяется орбитальным квантовым числом l :

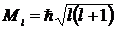, где l = 0,1,2,… n-1.

Квантуется также его проекция на некоторую заданную ось z, т.е. момент импульса электрона может иметь лишь такие ориентации в пространстве, для которых проекция 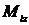принимает значения, кратные ћ: 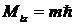, где m = 0,±1, ±2,…±l.

Таким образом, вектор собственного механического момента может принимать 2l +1 ориентацию в пространстве.

2.Спин электрона. В 1925 году Гаудсмит и Уленбек выдвинули гипотезу о том, что электрон обладает собственным механическим моментом импульса, не связанным с движением электрона в пространстве. Этот собственный момент был назван спином. Они дали спину наглядное модельное представление: спин – момент импульса, связанный с вращением электрона – заряженного шарика, вокруг своей оси. Однако скоро пришлось отказаться от подобных модельных представлений. Вращение электрона должно было бы происходить с такой угловой скоростью, что линейная скорость на поверхности его сферы в 200 раз превышала бы скорость света; либо размер электрона должен был превышать размеры атома; либо масса электрона превышала массу протона.

Спин и связанный с ним собственный (спиновый) магнитный момент следует считать внутренними свойствами, присущими электрону, подобно тому, как ему присущи заряд и масса. В отличие от орбитального момента спин всегда сохраняется. Спином обладают не только электроны, но и другие элементарные частицы – протоны, нейтроны, фотоны и др., кроме мезонов.

Величина собственного момента импульса электрона определяется по общим законам квантовой механики так называемым спиновым квантовым числомs

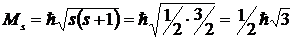, где .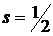

Проекция спина на заданное направление может принимать квантованные значения, отличающиеся друг от друга на ħ

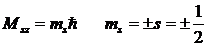
С собственным механическим моментом связан собственный магнитный момент. Ряд опытных фактов свидетельствовал, что отношение собственных магнитного и механического моментов равно

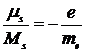
Отсюда собственный магнитный момент электрона равен

,

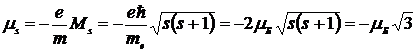Знак минус указывает на то, что механический и магнитный моменты электрона направлены в противоположные стороны.

Проекция собственного магнитного момента электрона на заданное направление может иметь следующие значения

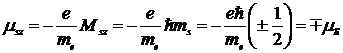
Таким образом, проекция собственного момента импульса электрона может принимать значения 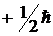и 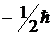, а собственного магнитного момента – значения 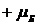и .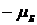

В ряд формул входят не сами моменты, а их проекции, поэтому принято говорить, что спин электрона равен одной второй (подразумевается в единицах ħ), а собственный магнитный момент равен одному магнетону Бора.

Магнитный момент атома складывается из орбитальных и собственных моментов входящих в его состав электронов, а также магнитного момента ядра (который обусловлен магнитными моментами входящих в состав ядра элементарных частиц). Магнитный момент ядра значительноменьше моментов электронов, поэтому при рассмотрении многих вопросов им можно пренебречь и считать, что момент атома равен векторной сумме магнитных моментов электронов.

3.Опыт Штерна и Герлаха.Посмотрим, каким образом можно было бы непосредственно убедиться в существовании спина и магнитного момента электрона. Очевидно, что для этого необходимо подвергнуть электрон действию внешнего магнитного поля. Наиболее подходящими для этой цели являются атомы водорода и элементов первой группы периодической системы. Невозбужденные состояния этих атомов принадлежат к типу s –состояний, т.е. орбитальный момент их равен нулю. Если опыт покажет, что эти атомы все-таки имеют механический и магнитный моменты, то их наличие можно приписать свойствам самого валентного электрона. Такой опыт был поставлен Штерном и Герлахом.

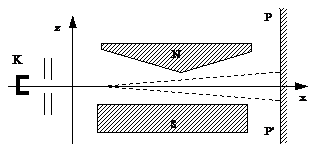
В закрытый сосуд помещали маленькую печку К, куда клали кусочек серебра. При нагревании серебро испарялось, и атомы его вылетали из отверстия печки во всевозможных направлениях с тепловыми скоростями порядка нескольких сот метров в секунду. С помощью нескольких щелей выделяли узкий пучок атомов серебра – атомный луч, который проходил через сильно неоднородное магнитное поле между полюсами электромагнита SN и попадал на пластину РР, где можно было обнаружить след осевших атомов. В неоднородном магнитном поле на атомы пучка должна действовать сила

,

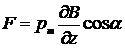величина и знак которой зависят от угла α, образуемого вектором 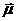с направлением поля. При хаотическом распределении моментов атомов по направлениям в пучке имеются частицы, для которых значения α изменяются в пределах от 0 до π. В соответствии с этим предполагалось, что узкий пучок атомов после прохождения между полюсами образует на экране сплошной растянутый след вследствие с различной ориентацией магнитных моментов. Опыт дал неожиданные результаты. Вместо сплошного растянутого следа получились две отдельные линии, расположенные симметрично относительно следа пучка, полученного в отсутствие поля.

Таким образом, опыт Штерна и Герлаха показал, что углы, под которыми ориентируются магнитные моменты атомов по отношению к магнитному полю, могут иметь только дискретные значения, т.е. проекция магнитного момента на направление поля квантуется.

Опыт, впервые поставленный с серебром, был проделан затем с атомами других веществ. Опыт показал, что в случае водорода, серебра и щелочных металлов возникают две полоски, расположенные симметрично относительно полоски, которая получается в отсутствие поля. Это свидетельствует о том, что при прохождении через поле пучок разбивается на два пучка, одинаково отклоняющиеся в противоположные стороны. То есть проекция собственного момента импульса электрона может принимать только два значения, одинаковых по величине и противоположных по знаку. При отсутствии у электрона спина в s-состоянии расщепление пучка не наблюдалось бы, так как орбитальный магнитный момент атома в этом случае равен нулю. Таким образом в опыте было доказано существование спина. Расчет проекции магнитного момента атома на направление поля показал, что он равен численно одному магнетону Бора.

Опыт Штерна и Герлаха наряду с немногими другими принадлежит к числу основных опытов атомной физики, так как он обнаруживает одно из важнейших свойств материи.

Вопросы для самоконтроля

1.В чем заключается квантование момента импульса?

2.Что такое спин? Имеет ли он классический аналог?

3.Какова схема опыта Штерна и Герлаха?

4.Что подтвердил опыт Штерна и Герлаха?

Лекция 9

МНОГОЭЛЕКТРОННЫЕ АТОМЫ

План

1. Принцип Паули. Распределение электронов на энергетических уровнях.

2. Периодическая система Д.И.Менделеева.

1.Принцип Паули. В связи с существованием спина электрона к квантовым числам добавляется квантовое число m_s, которое определяет проекцию спина на заданное направление. Число m_s, по аналогии с m, нужно было бы называть магнитным спиновым числом. Однако такое название обычно редко применяется. Число m_s отличается от спинового квантового числа s только тем, что принимает два значения ±½.Обычно, говоря о спиновом квантовом числе, понимают под ним число m_s.

Таким образом, состояние каждого электрона в атоме характеризуется четырьмя квантовыми числами:

главным n = 1, 2, 3,…

орбитальным l = 0, 1, 2, 3,… n-1

магнитным m = -l,…-1, 0, +1,…+l

спиновым m_s = +½, -½

На первый взгляд, если атом находится в невозбужденном состоянии, то все электроны атома должны заполнить уровень с наименьшей возможной энергией. Было установлено, что это не так. По мере увеличения порядкового номера атома Z происходит последовательное строго определенное заполнение электронных уровней атома.

Распределение электронов на энергетических уровнях. Порядок заполнения уровней предложил Паули. В 1925 году он установил квантово-механический закон, называемый принципом Паули:

В любом атоме не может быть двух электронов, находящихся в двух одинаковых стационарных состояниях, определяемых набором четырех квантовых чисел: главного n, орбитального l, магнитного m и спинового m_s.

Применительно к системе электронов в атоме принцип Паули можно записать следующим образом.

Число электронов, находящихся в состояниях, определяемых набором четырех квантовых чисел n, l, m и m_s:

Z₁(n,l,m,m_s) = 0 или 1.

Число электронов, находящихся в состояниях, определяемых набором трех квантовых чисел n, l и m:

Z₂(n,l,m) = 2

Эти электроны отличаются лишь ориентацией спинов, т.е. +½ħ или -½ħ

Число электронов, находящихся в состояниях, определяемых набором двух квантовых чисел n и l:

Z₃(n,l) = 2(2l+1)

Так как при заданном числовом значении момента импульса, он может принимать 2l+1 различных ориентаций в пространстве.

Число электронов, находящихся в состояниях, определяемых значением главного квантового числа n:

Z(n) = .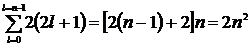

Совокупность электронов, имеющих одинаковые значения квантового числа n, образует электронный слой.

Слои подразделяются на оболочки,отличающиеся значением квантового числа l.

В соответствии со значением n слоям дают следующие обозначения:

Значение n	1 2 3 4 5 6 7 …
Обозначение слоя	K L M N O P Q …

Нарисуем таблицу, в которой определим максимальные числа электронов, находящихся в состояниях, характеризуемых данными значениями главного и орбитального квантовых чисел

Слой	Число электронов в оболочках	Максимальное число электронов
s (l = 0)	p (l = 1)	d (l = 2)	f (l = 3)	g (l = 4)
K		-	-	-	-
L			-	-	-
M				-	-
N					-
O

Принцип Паули сыграл выдающуюся роль в развитии современной атомной и ядерной физики. Так, например, удалось теоретически обосновать периодическую систему элементов Менделеева. Без принципа Паули невозможно было бы создать квантовые статистики и современную теорию твердых тел.

2.Периодическая система элементов Менделеева. В 1869 году Менделеев открыл периодический закон изменения химических и физических свойств элементов в зависимости от их атомных масс.

Если расположить химические элементы в порядке возрастания их атомных масс, то периодически, через правильные промежутки, называемые периодами, элементы, оказавшиеся в одном вертикальном ряду (группе) обнаруживают сходные физико-химические свойства.

Однако в ряде случаев приходилось отступать от принципа возрастания атомных масс. Менделеев ввел понятие о порядковом номере элемента, расположив известные в его время 64 химических элемента в таблицу в порядке возрастания их номера. Часть клеток периодической таблицы оставалась свободной, так как не все элементы были известны к тому времени. Таким образом, Менделееву удалось на основании открытого им закона предсказать ряд новых химических элементов (галлий, скандий, германий и т. д.) и описать их химические свойства. В дальнейшем все эти элементы были открыты и предсказания Менделеева полностью подтвердились.

Физический смысл порядкового номера Z элемента в периодической системе элементов был установлен в ядерной модели Резерфорда: Z совпадает с числом положительных заряженных частиц в ядре, закономерно возрастающим на единицу при переходе от элемента к элементу.

Химические свойства элементов и ряд их физических свойств объясняются поведением внешних, валентных электронов атомов этих элементов. Поэтому периодичность свойств химических элементов должна быть связана с определенной периодичностью в расположении электронов в атомах различных элементов.

Важнейшей задачей физики явилось теоретическое истолкование периодического закона Менделеева и объяснение строения периодической системы.

Теория периодической системы основывается на следующих положениях квантовой механики:

1. Порядковый номер химического элемента равен общему числу электронов в атоме данного элемента;

2. Состояние электронов в атоме определяется набором их квантовых чисел n, l, m и m_s. Распределение электронов в атоме по энергетическим состояниям должно удовлетворять принципу минимума потенциальной энергии: с возрастанием числа электронов каждый следующий электрон должен занять возможное энергетическое состояние с наименьшей энергией;