Фарадеевская и максвелловская трактовки явления электромагнитной индукции. Ток смещения.
Из закона электромагнитной индукции Фарадея следует
ℇ 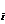 = -dФ/dt,
= -dФ/dt,
где ℇ 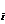 - ЭДС электромагнитной индукции; dФ/dt, - скорость изменения магнитного потока. В фарадеевской трактовке при изменении магнитного потока, пронизывающего некоторый проводящий контур, в нем возникает ЭДС и индукционный ток. Максвелл предположил, что изменяющееся со временем магнитное поле обуславливает появление в пространстве электрического поля независимо от присутствия в этом пространстве проволочного контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля.
- ЭДС электромагнитной индукции; dФ/dt, - скорость изменения магнитного потока. В фарадеевской трактовке при изменении магнитного потока, пронизывающего некоторый проводящий контур, в нем возникает ЭДС и индукционный ток. Максвелл предположил, что изменяющееся со временем магнитное поле обуславливает появление в пространстве электрического поля независимо от присутствия в этом пространстве проволочного контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля.
Итак, согласно идее Максвелла изменяющееся со временем магнитное поле порождает электрическое поле. Это поле существенно отличается от порождаемого неподвижными зарядами электростатического поля. Электростатическое поле потенциально, его силовые линии начинаются и заканчиваются на зарядах. Электрическое поле, создаваемое переменным магнитным полем вихревое, его силовые линии замкнуты.
В 1865 г. Максвелл высказал гипотезу о том, что изменение электрического поля должно вызывать образование магнитного поля. В дальнейшем эта гипотеза нашла экспериментальное подтверждение.
Переменное электрическое поле, которое может создавать переменное магнитное поле, Максвелл назвал током смещения.
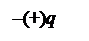
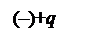 Рассмотрим цепь переменного тока, содержащую конденсатор (рис.
Рассмотрим цепь переменного тока, содержащую конденсатор (рис.
 30.1). Между обкладками заряжающегося и разряжающегося конденса-
30.1). Между обкладками заряжающегося и разряжающегося конденса-

Рис. 30.1 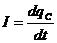 (30-1)
(30-1)
Так как 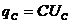 (С - емкость конденсатора,
(С - емкость конденсатора, 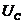 - напряжение на нем)
- напряжение на нем)
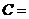 ℰℰ
ℰℰ 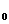 S/ℓ (здесь кроме известных обозначений ℓ - расстояние ме- жду пластинами конденсатора)
S/ℓ (здесь кроме известных обозначений ℓ - расстояние ме- жду пластинами конденсатора)
Напряжение на конденсаторе 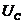 можно представить как произведение напряженности электрического поля внутри конденсатора на расстояние между пластинами, то есть
можно представить как произведение напряженности электрического поля внутри конденсатора на расстояние между пластинами, то есть 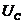 = Е⋅ℓ, подставляя в (30 -1), получим
= Е⋅ℓ, подставляя в (30 -1), получим
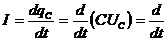 (Еℓ⋅ℰℰ
(Еℓ⋅ℰℰ 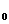 S/ℓ) = S⋅d(ℰℰ
S/ℓ) = S⋅d(ℰℰ 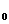 E)/dt
E)/dt
Выражение в скобках ℰℰ 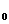 E = D – электрическое смещение, то есть
E = D – электрическое смещение, то есть
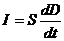
Разделим обе части на S, тогда в левой части будет плотность тока 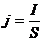 , а в правой -
, а в правой - 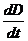 , то есть
, то есть 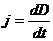 . Так как в общем случае
. Так как в общем случае 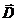 может иметь производные по координатам, запишем j через частную производную по времени
может иметь производные по координатам, запишем j через частную производную по времени 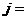
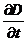 или в векторной форме
или в векторной форме
|
Эта величина получила название плотности тока смещения. Ток смещения находится интегрированием.






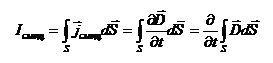
(30-2)
При этом еще раз отметим, что никакого тока между пластинами конденсатора нет, а есть переменное электрическое поле. Название «ток смещения» является условным, исторически сложившемся (так назвал Максвелл).






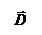
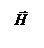














 По Максвеллу переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между
По Максвеллу переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между

т.е. вектор 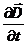 направлен противоположно вектору
направлен противоположно вектору 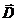 , а вектор
, а вектор 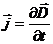 имеет такое направление, что как бы «продолжает» направление тока в подводящих проводах.
имеет такое направление, что как бы «продолжает» направление тока в подводящих проводах.
Максвелл ввел понятие полного тока, равного сумме токов проводимости и смещения. Плотность полного тока
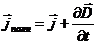 (30-3)
(30-3)
