Переходный процесс в электрической цепи, описываемой дифференциальным уравнением 2-го порядка.
Рассмотрим процесс включения электрической цепи, содержащей сопротивление, индуктивность и емкость.
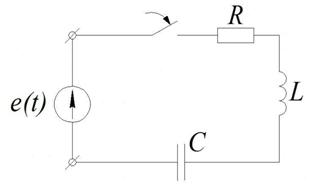
Дифференциальное уравнение, связывающее ЭДС и ток в такой цепи имеет следующий вид:
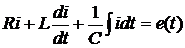 или
или
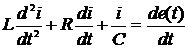 .
.
Переходный ток ищем в виде суммы принужденной и свободной составляющих
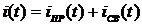 , где
, где
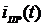 определяется исходя из характера e(t), а
определяется исходя из характера e(t), а 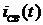 ищется в виде суммы экспонент
ищется в виде суммы экспонент
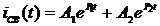 .
.
Таким образом
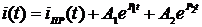 , где
, где
р1 и р2 – корни характеристического уравнения, а А1 и А2 – постоянные интегрирования.
Характеристическое уравнение имеет вид:
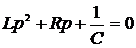 или
или
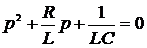 .
.
Находим корни характеристического уравнения:
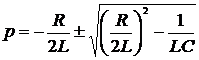 .
.
Введем обозначения
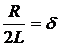 ;
; 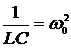 , тогда
, тогда
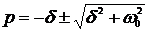 .
.
Для определения постоянных интегрирования необходимо знать характер e(t).
Пусть e(t)=E – const, т.е. рассматриваем включение цепи R, L, C к источнику постоянной ЭДС.
1) Определим 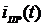 . Т.к. цепь содержит емкость и включается к источнику постоянной ЭДС то
. Т.к. цепь содержит емкость и включается к источнику постоянной ЭДС то 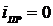 .
.
2) Запишем переходный ток
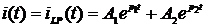 .
.
3) Определим независимые начальные условия
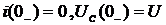
4) По законам коммутации
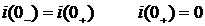
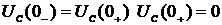
5) При t=0 имеем:
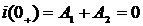 .
.
6) Вычислим 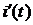 .
.
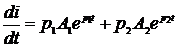
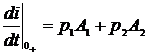
7) Таким образом, для определения постоянных интегрирования имеем систему из двух уравнений с двумя неизвестными.
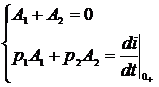
8) Определим 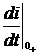 (зависимое начальное условие) по закону Кирхгофа.
(зависимое начальное условие) по закону Кирхгофа.
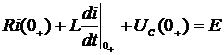 . Т.к.
. Т.к. 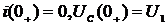 , то
, то
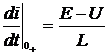
9) Определим А1 и А2.
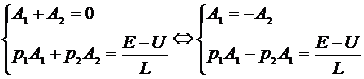
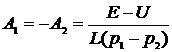
10) Запишем переходной ток.
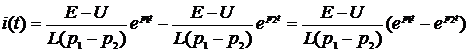
Проанализируем поведение переходного тока при различных соотношениях между корнями характеристического уравнения.
1) Корни вещественные и различные, т.е. р1≠р2.
р1>р2
Т.к. 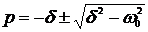 то в этом случае
то в этом случае
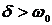 , т.е.
, т.е. 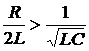 ,
, 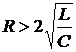 .
.
Тогда: 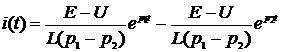
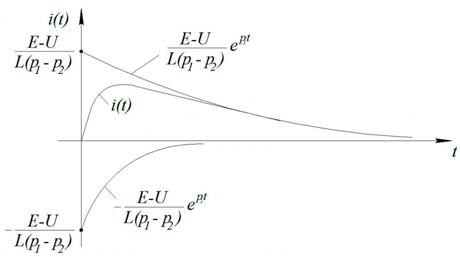
Такой характер переходного тока называется апериодическим.
2) Корни вещественные и равные, т.е. 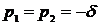 .
.
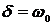 ;
; 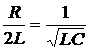 ;
; 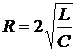 .
.
Подстановка корней р1=р2=р в выражение для переходного тока приводит к неопределенности вида 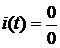 .
.
Раскрывая неопределенность по правилу Лопиталя, получаем:
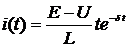
К этому же выражению приходим, рассматривая общее решение однородного уравнения с кратными корнями:
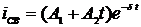 .
.
Найдем А1 и А2.
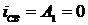 , т.к.
, т.к. 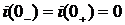 и
и 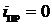 .
.
Тогда 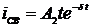 .
.
Вычислим производную 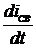 .
.
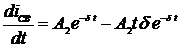 .
.
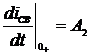 , но
, но 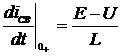 (определялось нами ранее).
(определялось нами ранее).
Таким образом, 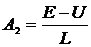 .
.
Окончательно получаем:
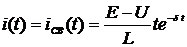 .
.
Эта функция с одной стороны линейно возрастает с возрастанием t ,а с другой стороны убывает по экспоненциальному закону 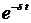 .
.
При малых значениях t возрастание по линейному закону имеет большее значение, чем убывание по экспоненциальному. При больших значениях t убывание по экспоненциальному закону становится преобладающим.
Таким образом, переходный ток с течением времени возрастает, достигает максимума, а затем убывает.
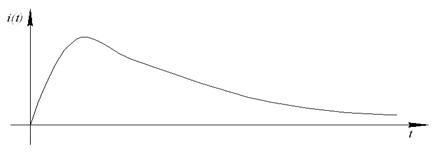
При этом процесс остается апериодическим.
3) Корни комплексно-сопряженные.
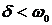 ;
; 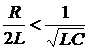 ;
; 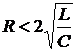 .
.
Тогда 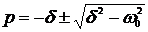 .
.
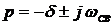 , где
, где 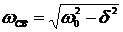 - частота свободных колебаний, откуда
- частота свободных колебаний, откуда 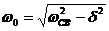 .
.
Рассматривая корни в комплексной плоскости, устанавливаем, что они расположены в левой полуплоскости на дуге окружности с радиусом, равным 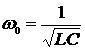 .
.
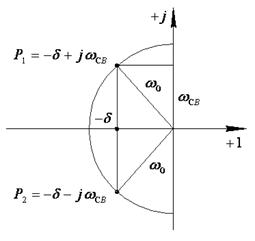
Определим переходный ток в цепи:
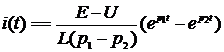 , где
, где
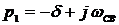 ;
; 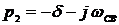 .
.
После подстановки значений корней р1 и р2 получаем:
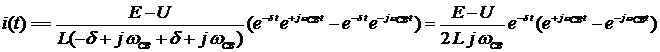
Учитывая, что 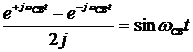 , получаем:
, получаем:
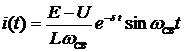 .
.
Полученное выражение показывает, что в цепи возникают колебания с угловой частотой 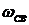 . Амплитуда этих колебаний, равная
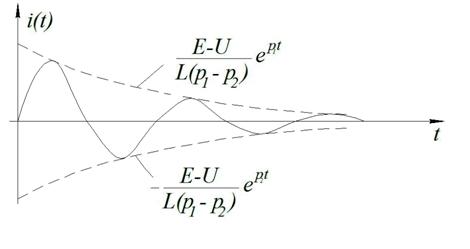
. Амплитуда этих колебаний, равная 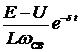 , убывает по экспоненциальному закону, т.е. рассматриваемые колебания являются затухающими.
, убывает по экспоненциальному закону, т.е. рассматриваемые колебания являются затухающими.
Подведем некоторые итоги:
1) Если 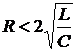 , то переходный процесс перестает быть апериодическим и имеет колебательный характер. Частота
, то переходный процесс перестает быть апериодическим и имеет колебательный характер. Частота 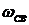 называется угловой частотой свободных или собственных колебаний в цепи R, L, C.
называется угловой частотой свободных или собственных колебаний в цепи R, L, C. 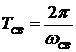 - период этих колебаний.
- период этих колебаний.
2) Сопротивление 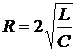 , при котором характер переходного процесса все еще остается апериодическим, называется критическим сопротивлением.
, при котором характер переходного процесса все еще остается апериодическим, называется критическим сопротивлением.
3) О характере переходного процесса можно судить по корням характеристического уравнения или по их расположению на комплексной плоскости.
4) Если корни характеристического уравнения отрицательные, вещественные и различные (располагаются на вещественной оси в левой полуплоскости), то переходный процесс имеет апериодический характер.
5) Если корни характеристического уравнения отрицательные, вещественные и равные (располагаются в одной и той же точке вещественной оси в левой полуплоскости), то переходный процесс еще сохраняет апериодический характер.
6) Если корни характеристического уравнения комплексно-сопряженные (располагаются в левой полуплоскости на полуокружности с радиусом 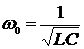 ), характер переходного процесса – затухающие колебания. Колебания в цепи возникают вследствие периодического преобразования энергии электрического поля в энергию магнитного поля и обратно, причем эти колебания сопровождаются потерей в сопротивлении.
), характер переходного процесса – затухающие колебания. Колебания в цепи возникают вследствие периодического преобразования энергии электрического поля в энергию магнитного поля и обратно, причем эти колебания сопровождаются потерей в сопротивлении.
Величина 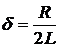 называется коэффициентом затухания. При времени
называется коэффициентом затухания. При времени 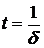 амплитуда колебаний в «е» раз меньше начального значения. Следовательно,
амплитуда колебаний в «е» раз меньше начального значения. Следовательно, 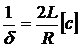 - является постоянной времени цепи R, L, C.
- является постоянной времени цепи R, L, C.
Чем меньше 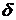 по сравнению с
по сравнению с 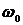 , тем медленнее затухают колебания и тем больше частота
, тем медленнее затухают колебания и тем больше частота 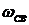 приближается к резонансной частоте
приближается к резонансной частоте 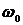 .
.
В пределе, при 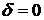
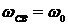 . Колебания не затухают, а корни характеристического уравнения становятся чисто мнимыми и располагаются на мнимой оси комплексной плоскости.
. Колебания не затухают, а корни характеристического уравнения становятся чисто мнимыми и располагаются на мнимой оси комплексной плоскости.
О быстроте затухания колебательного процесса судят по величине 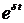 , где t=TCB. Величина
, где t=TCB. Величина 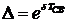 называется декрементом колебания (от лат. decrementum – затухание, уменьшение).
называется декрементом колебания (от лат. decrementum – затухание, уменьшение).
Натуральный логарифм этой величины называется логарифмическим декрементом колебания, т.е. 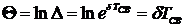 .
.
Декремент колебания можно определить по графику переходного процесса, как отношение двух амплитуд колебания, отстоящих одна от другой на период свободных колебаний.
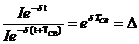 ;
; 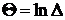 .
.
