Опыты Фарадея. Закон Фарадея. Правило Ленца. ЭДС индукции в неподвижных проводниках.

1. Опыты Фарадея

а) В соленоид, замкнутый на гальванометр, вдвигается и выдвигается постоянный магнит. На гальванометре будет отклонение стрелки, и оно будет тем больше, чем быстрее происходит вдвижение и выдвижение. При изменении полюсов магнита направление отклонения стрелки изменится.

б) В соленоид, замкнутый на гальванометр, вставлена катушка (другой соленоид), через которую пропускается ток. При включении и выключении (т.е. при любом изменении тока) происходит отклонение стрелки гальванометра. Направление отклонения изменяется при включении – выключении, уменьшении – увеличении тока, вдвигании – выдвигании катушек.

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает индукционный (наведенный) электрический ток.

Возникновение индукционного тока означает, что в контуре действует электродвижущая сила _i – ЭДС индукции.

ЭДС индукции, возникающая в проводящем контуре, равна скорости изменения магнитного потока через площадь, ограниченную этим контуром – закон Фарадея.

Правило Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.

Знак минус в законе Фарадея является математическим выражением правила Ленца.

Если контур, в котором индуцируется ЭДС, состоит не из одного витка, а из N витков (например, соленоид), то если витки соединены последовательно, _i будет равна сумме ЭДС, индуцируемых в каждом из витков в отдельности:

- потокосцепление или полный магнитный поток.

Если Ф₁ =Ф₂=…=Ф_n, то

Т.к. Ф_B=BScosα,то для того чтобы изменить магнитный поток Ф можно изменить:

1) магнитное поле 2) площадь S3) угол α.

Индуктивность соленоида.

Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока (или магнитная индукция) 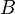, которая выражается в системе СИ в тесла [Тл], внутри катушки является фактически постоянной и (приближённо) равна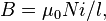

где 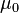− магнитная постоянная, 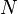− число витков, 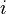− ток, записанный в амперах [А] и 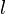− длина катушки в метрах [м]. Пренебрегая краевыми эффектами на концах соленоида, получим^[16], что потокосцепление через катушку равно плотности потока 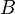[Тл], умноженному на площадь поперечного сечения 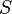[м²] и число витков :

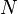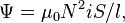
Отсюда следует формула для индуктивности соленоида (без сердечника):

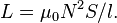
Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель 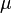— относительную магнитную проницаемость^[17] сердечника:

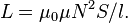
В случае, когда 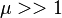, можно (следует) под S понимать площадь сечения сердечника [м²] и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.