Закон Джоуля-Ленца в интегральной и дифференциальной формах.

Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов 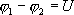, тогда работу по переносу заряда q на этом участке равна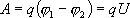

По определению I= q/t. откуда q= I t. Следовательно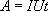

Так как работа идет на нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил

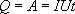
Это соотношение выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности 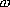, равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника

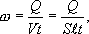
где S - поперечное сечение проводника, 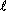- его длина.

Используя соотношение 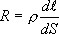, получим

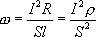
Но 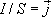- плотность тока, а 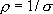, тогда

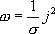
с учетом закона Ома в дифференциальной форме 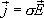, окончательно получаем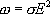

Эта формула выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.

Магнитное поле. Вектор магнитной индукции и вектор напряженности магнитного поля. Закон Ампера. Принцип суперпозиции магнитных полей.

Магнитное поле

Опыт показывает, что, подобно тому, как в пространстве, окружающем электрические заряды, возникает электростатическое поле, так и в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные магниты. Название «магнитное поле» связывают с ориентацией магнитной стрелки под действием поля, создаваемого током (это явление впервые обнаружено датским физиком X. Эрстедом (1777—1851)).

Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды. Важнейшая особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды. Опыт показывает, что характер воздействия магнитного поля на ток различен в зависимости от формы проводника, по которому течет ток, от расположения проводника и от направления тока. Следовательно, чтобы охарактеризовать магнитное поле, надо рассмотреть его действие на определенный ток.

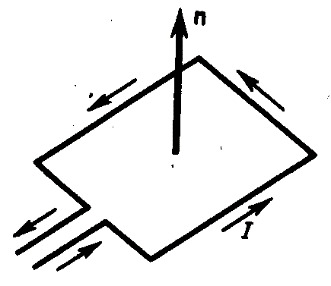Подобно тому, как при исследовании электростатического поля использовались точечные заряды, при исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), линейные размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле. Ориентация контура в пространстве определяется направлением нормали к контуру. Направление нормали определяется правилом правого винта: за положительное направление нормали принимается направление поступательного движения винта, головка которого вращается в направлении тока, текущего в рамке.

Опыты показывают, что магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая ее определенным образом. Этот результат используется для выбора направления магнитного поля. За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к рамке

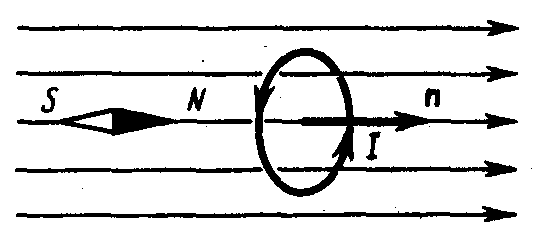
За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса магнитной стрелки лежат в близких точках поля, то силы, действующее на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направлением поля.

Вектор магнитной индукции и вектор напряженности магнитного поля.

Рамкой с током можно воспользоваться также и для количественного описания магнитного поля. Так как рамка с током испытывает ориентирующее действие поля, то на нее в магнитном поле действует пара сил. Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки и определяется формулой

M = [p_mB](109.1)

где pm— вектор магнитного момента рамкис током (В— вектор магнитной индукции,количественная характеристика магнитного поля). Для плоского контура с током I

p_m=ISn(109.2)

где S — площадь поверхности контура (рамки), n— единичный вектор нормали к поверхности рамки. Направление рm совпадает, таким образом, с направлением положительной нормали.

Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют различные вращающие моменты, однако отношение Мmax/рm (Мmax — максимальный вращающий момент) для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля, называемой магнитной индукцией:

B = M_max/p_m

Магнитная индукцияв данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля. Следует отметить, что вектор Вможет быть выведен также из закона Ампера (с м. § 111) и из выражения для силы Лоренца (см. § 114).

Так как магнитное поле является силовым, то его, по аналогии с электрическим, изображают с помощью линий магнитной индукции— линий, касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.

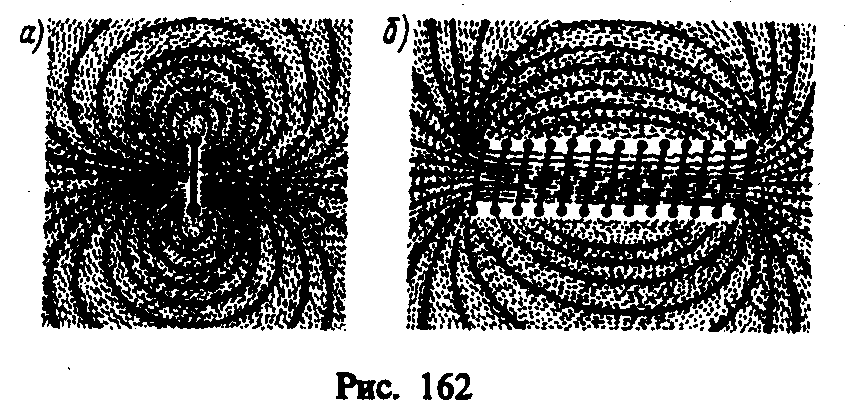Линии магнитной индукции можно «проявить» с помощью железных опилок, намагничивающихся в исследуемом поле и ведущих себя подобно маленьким магнитным стрелкам. На рис. 162, а показаны линии магнитной индукции поля кругового тока, на рис. 162, б — линии магнитной индукции поля соленоида (соленоид — равномерно намотанная на цилиндрическую поверхность проволочная спираль, по которой течет электрический ток).

Линии магнитной индукции всегда замкнуты и охватывают проводники с током. Этим они отличаются от линий напряженности электростатического поля, которые являются разомкнутыми (начинаются на положительных зарядах и кончаются на отрицательных (см. § 79)).

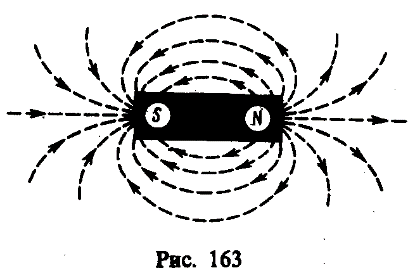
На ряс. 163 изображены линии магнитной индукции полосового магнита; они выходят из северного полюса и входят в южный. Вначале казалось, что здесь наблюдается полная аналогия с линиями напряженности электростатического поля и полюсы магнитов играют роль магнитных «зарядов» (магнитных монополей). Опыты показали, что, разрезая магнит на части, его полюсы разделять нельзя, т. е. в отличие от электрических зарядов свободные магнитные «заряды» не существуют, поэтому линии магнитной индукции не могут обрываться на полюсах. В дальнейшем было установлено, что внутри полосовых магнитов имеется магнитное поле, аналогичное полю внутри соленоида, и линии магнитной индукции этого магнитного поля являются продолжением линий магнитной индукции вне магнита. Таким образом, линии магнитной индукции магнитного поля постоянных магнитов являются также замкнутыми.

До сих пор мы рассматривали макроскопические токи, текущие в проводниках. Однако, согласно предположению французского физика А. Ампера (1775—1836), в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Эти микроскопические молекулярные токи создают свое магнитное поле и могут поворачиваться в магнитных полях макротоков. Например, если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле. Вектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, т. е. при одном и том же токе и прочих равных условиях векторВвразличных средах будет иметь разные значения.

П09.3)

Магнитное поле макротоковописывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:

B = μ₀μH

где μ0 — магнитная постоянная, μ — безразмерная величина — магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоковН усаливается за счет поля микротоков среды.

Сравнивая векторные характеристики электростатического (Еи D) и магнитного (Ви Н) полей, укажем, что аналогом вектора напряженности электростатического поляЕявляется вектор магнитной индукции В, так как векторы Еи Вопределяют силовые действия этих полей и зависят от свойств среды. Аналогом вектора электрического смещения Dявляется вектор напряженности Нмагнитного поля.

Закон Ампера.

Магнитное поле (см. § 109) оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током. Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dlс током, находящегося в магнитном поле, равна

dF = I[dl, B](111.1)

где dl—вектор, по модулю равный dlи совпадающий по направлению с током, В— вектор магнитной индукции.

Направление вектора dFможет быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правило левой руки:если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера (см. (111.1)) вычисляется по формуле

dF = IBdlsina(111.2)

где a — угол между векторами dlи В.

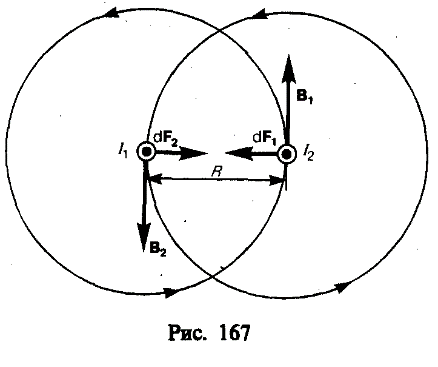Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2; (направления токов указаны на рис. 167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I1 на элемент dlвторого проводника с током I2. Ток I1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора B1 определяется правилом правого винта, его модуль по формуле 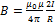(110.5) равен

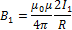
Направление силы dF1, с которой поле B1 действует на участок dlвторого тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол  между элементами тока I2 и вектором B1 прямой, равен

dF₁ = I₂B₁dl

подставляя значение для В1, получим

dF₁ = 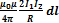(111.3)

Рассуждая аналогично, можно показать, что сила dF2 с которой магнитное поле тока I2 действует на элемент dlпервого проводника с током I1, направлена в противоположную сторону и по модулю равна

dF₂ =I₁B₂dl = 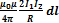(111.4)

Сравнение выражений (111.3) и (111.4) показывает, что

dF₁ = dF₂

т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой

dF = 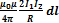(111.5)

Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5).