Туннельный эффект. Коэффициент прозрачности барьера

Туннельный эффект - преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительно квантовой природы, невозможное в классической механике; аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрения геометрической оптики, происходит полное внутреннее отражение.

Коэффициент прозрачности барьера D: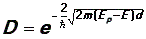

Коэффициент прозрачности характеризует вероятность прохождения частицы сквозь барьер. Эта вероятность очень сильно зависит от толщины барьера d: чем толще барьер, тем меньше вероятность туннельного эффекта.

15. Гармонический осциллятор. Квантовомеханическое описание атома водорода.

Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы 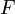, пропорциональной смещению 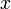(согласно закону Гука):

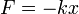
где 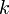— коэффициент жёсткости системы.

Если 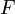— единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Важнейший постулат Н.Бора был сформулирован так: "Двигаясь по дозволенным орбитам в атоме водорода, электрон не излучает и не поглощает энергии". Но это противоречило классической электродинамике. Если классическая электродинамика не применима к атомам, то надо создавать механику для электронно-ядерных систем атомных масштабов, т.е. надо создавать квантовую механику.

Такая механика была создана усилиями двух независимых групп ученых: В.Гайзенберг и М.Борн в Германии основное уравнение квантовой механики записали в матричной форме, а Э.Шредингер (который по существу лишь завершил большую предварительную работу, проделанную Л.Больцманом, М.Планком, А.Энштейном и Луи де Боройлем) предложил уравнение, учитывающие не только все электростатические взаимодействия электронно-ядерных систем, но и волновые свойства электронов.

Одним из важнейших современных методов исследования строения атомов и молекул является квантовая механика. Пусть, например, нас интересует строение атома водорода и ионов He+, Li2+, Be3+ и т.д., т.е. одноэлектронных и одноядерных систем. Для того чтобы решить эту задачу квантовая механика должна записать Уравнение Шредингера для этой системы и решить его. Прежде всего необходимо учесть потенциальную энергию взаимодействия всех составных частей системы, в нашем случае электрона и ядра:

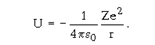
Волновые свойства электрона Уравнение Шредингера учитывает автоматически. Математики задолго до 1926 г. изучили дифференциальные уравнения подобного типа и тщательно разработали методы их решения. Исходя из физического смысла решаемой задачи нужно потребовать, чтобы волновая функция, характеризующая всю совокупность свойств рассматриваемой электронно-ядерной системы, была непрерывной, конечной и однозначной. Это уравнение решается, если некоторые параметры n, l, m (квантовые числа) принимают определенные целочисленные значения.

Главное квантовое число - n - может принимать значения 1, 2, 3, ..., оно характеризует электронный слой, в котором находится электрон, энергию электрона в этом слое, размеры пространства, в котором движется электрон, проявляя свои волновые свойства.Второе квантовое число - l называют побочным или орбитальным квантовым числом. Оно характеризует орбитальный момент количества движения электрона при его движении в слое n и может принимать численные значения 0, 1, 2, ... и вплоть до максимального n-1. Чтобы было удобно выражать сразу набор квантовых чисел n и l, для последнего вместо чисел 0, 1, 2, 3, ... часто используются буквенные эквиваленты s, p, d, f, ... Так, сочетание 1s означает, что n=1, а l=0. Если n=2, а l=1, то пишут 2p. l характеризует форму орбитали, на которой находится электрон. Так, s-орбитали имеют форму шара,

p-орбитали имеют форму двух шаров, которые касаются друг друга в точке, где расположено ядро. Эти шары иногда изображают сильно вытянутыми и говорят, что p-орбиталь имеет форму гантели.

d-орбиталь имеет достаточно сложную пространственную форму, получаемую при перпендикулярном расположении двух гантелей.

Третье квантовое число - m называют магнитным. Оно определяет пространственную ориентацию момента количества движения электрона и принимает значения -l, -l+1, ..., 0, 1, ..., l, а всего 2l+1 значений.

Если для атома водорода решать не Уравнение Шредингера, а более точное уравнение Дирака, то появляется еще одно квантовое число - спиновое, которое может принимать всего два значения +1/2(a) и -1/2(b) и характеризует всего две возможные ориентации в пространстве собственного момента количества движения электрона (спина). Для изображения этого квантового числа часто используют стрелки, направленные вверх или вниз.

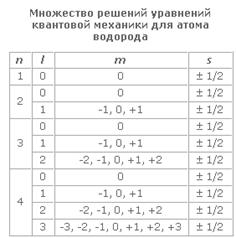Итак, все множество решений уравнений квантовой механики для атома водорода можно свести в таблицу. Может ли атомарный водород находиться в любом из тех состояний, которые представлены в этой таблице? Да, может. Атомы водорода с одинаковой вероятностью могут находиться в любом из этих состояний? Нет. В земных условиях, в межзвездном пространстве наиболее стабильным для водорода является состояние с минимальной энергией, т.е. 1s-состояние. Может ли атом водорода переходить из одного состояния в другое? Да, может. Что происходит при таком переходе? По мере увеличения значения главного квантового числа энергия атома возрастает. Поэтому в солнечной атмосфере или в разрядной трубке при прохождении электрического тока атомы водорода могут переходить из основного 1s состояния в возбужденные: 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f и т.д. Время жизни в возбужденных состояниях очень мало и, испуская квант света hn, который уносит избыточную энергию, атом водорода возвращается в менее возбужденные состояния, или в 1s-состояние.

16. Уровни энергии и схема термов щелочных металлов. Дублетная структура спектров щелочных металлов.

Спектры испускания атомов щелочных металлов, подобно спектру водорода, состоят из нескольких серий линий. Наиболее интенсивные из них получили названия: главная, резкая, диффузная и основная (или серия Бергмана). Эти названия имеют следующее происхождение. Главная серия названа так потому, что наблюдается и при поглощении. Следовательно, она соответствует переходам атома в основное состояние. Резкая и диффузная серии состоят соответственно из резких и размытых (диффузных) линий. Серия Бергмана была названа основной (фундаментальной) за свое сходство с сериями водорода.

Еще 'в конце прошлого столетия Ридберг установил эмпирические формулы, позволяющие вычислить частоты серий щелочных металлов. Эти формулы для всех серий сходны и имеют вид:

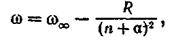
где 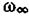—частота, соответствующая границе серии, 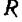— постоянная Ридберга (59,5), 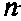—целое число, 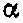—дробное число.

Таким образом, частоты линий могут быть представлены как разности двух термов: постоянного ( 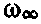) и переменного, имеющего более сложный вид, чем баль-меровский терм 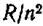. Константы 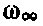и а для различных

серий имеют, вообще говоря, разное значение. Так, например, спектральные серии натрия можно представить следующими формулами.

Резкая серия(буква s является начальной буквой наименования серии: sharp — резкий).

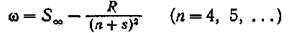
Главная серия:(principal — главный),

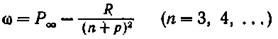
Диффузная серия:(diffuse — диффузный).

Основная серия (серия Бергмана)(fundamental — основной).:

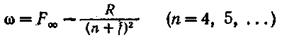
Вследствие равенства константы / нулю переменный терм в формуле для основной серии совпадает с баль-меровским, а сама серия, как уже отмечалось, является водородоподобной.

Для сокращения условились записывать переменные термы, указывая число п с добавлением букв S, P, D, Fсоответственно для каждой серии. Тогда переменный терм резкой серии вместо 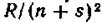будет иметь вид/zS.

Переменный терм главной серии запишется как пР₉ диффузной — nD и, наконец, основной — nF.

Переписывая формулы для серий натрия с использованием сокращенных обозначений, учтем также то обстоятельство, что, как было установлено экспериментально, постоянный терм главной серии Р^ оказался совпадающим с переменным термом резкой серии для п = 3 (Роо = 35). Постоянные термы £<» и /)<*> оказались одинаковыми и равными переменному терму главной серии для п = 3 (Soo — Dm = ЗР). Постоянный терм основной серии Foo оказался равным переменному терму диффузной серии для п = 3 {Foo — 3D). Таким образом, спектральные серии натрия могут быть представлены в следующем виде:

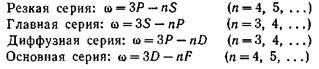
Мы пришли к весьма существенному результату. Выяснилось, что линии всех четырех спектральных серий можно получить путем комбинации четырех типов (рядов) термов: 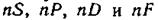[ср. с формулой (59.9)].

Терм с точностью до постоянного множителя совпадает с энергией соответствующего состояния атома [см. формулу (62.2)]. Следовательно, каждому ряду спектральных термов должен соответствовать свой ряд энергетических уровней. Эмпирическая схема уровней атома натрия изображена на рис. 200. Схемы уровней других щелочных металлов имеют такой же характер, как у натрия.

Схема уровней натрия (рис. 200) отличается от схемы уровней водородного атома (рис. 198) тем, что аналогичные уровни в различных рядах лежат на неодинаковой высоте. Несмотря на это отличие, обе схемы обнаруживают большое сходство. Это сходство дает основание предположить, что спектры щелочных металлов испускаются при переходах самого внешнего (так называемого валентного или опти ческого) электрона с одного уровня на другой.

Из рис. 200 видно, что энергия состояния оказывается зависящей, кроме числа п, также от того, в какой ряд попадает данный терм, т. е. от номера ряда термов. На схеме уровней атома водорода различные ряды термов (с совпадающими по высоте уровнями) отличаются значениями момента импульса электрона. Естественно предположить, что различные ряды термов щелочных металлов также отличаются значениями момента импульса оптического электрона. Поскольку уровни различных рядов в этом случае не лежат на одинаковой высоте, следует принять, что энергия оптического электрона в атоме щелочного металла зависит от величины момента импульса электрона (чего мы не наблюдали для водорода).

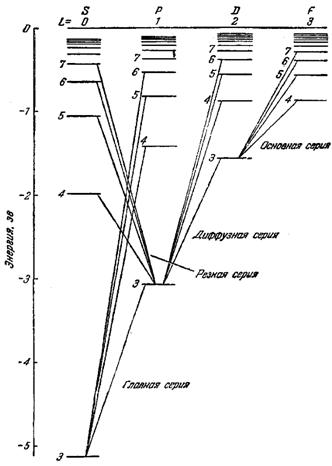
Рис. 200. В более сложных, чем водород, атомах, имеющих несколько электронов, можно считать, что каждый из электронов движется в усредненном поле ядра и остальных электронов. Это™'поле уже не будет кулоновским (т. е. пропорциональным 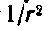), но обладает центральной симметрией (зависит только от г). В самом деле, в зависимости от степени проникновения электрона в глубь атома заряд ядра будет для данного электрона в большей или меньшей степени экранироваться другими электронами, так что эффективный заряд, воздействующий на рассматриваемый электрон, не будет постоянным. Вместе с тем, поскольку электроны движутся в атоме с огромными скоростями, усредненное по времени поле можно считать центрально-симметричным.

Решение уравнения Шредингера (65.3) для электрона, движущегося в центрально-симметричном некуло-новском поле, дает результат, аналогичный результату для водородного атома, с тем отличием, что энергетические уровни зависят не только от квантового числа п, но и от квантового числа l:

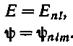
Таким образом, в этом случае снимается вырождение по /. Отличие в энергии между состояниями с различными / и одинаковыми п вообще не так велико, как между состояниями с различными п. С увеличением / энергия уровней с одинаковыми п возрастает.

Числа / и т по-прежцему определяют момент импульса электрона и его проекцию на заданное направление.

Момент импульса атома в целом слагается из моментов всех электронов, входящих в состав атома. Сложение моментов импульса осуществляется по квантовым "законам, согласно которым величина результирующего момента Мопределяется выражением:

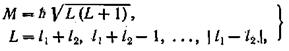(70.2)

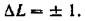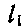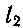(70.3) где и —числа, определяющие складываемые моменты Mi и М₂ по формуле: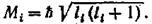

Таким образом, результирующий момент может иметь 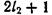или 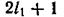(нужно взятъ меньшее из двух /) различных значений.

Исследования оптических спектров ионов щелочных металлов показали, что мЪмент импульса атомного остатка (т. е. ядра и остальных электронов, кроме наименее связанного 'оптического электрона, удаляющегося при ионизации) равен нулю. Следовательно, момент атома щелочного металла равен моменту его оптического электрона и L атома совпадает с / этого электрона.

Поскольку при возбуждении атома и испускании света остальные электроны не изменяют своего энергетического состояния, схему уровней атома можно считать тождественной схеме уровней оптического электрона. Таким образом, квантовая механика объясняет все особенности приведенной на рис. 200 схемы.

На рис. 200 показаны переходы между уровнями, приводящие к возникновению различных серий. Эти переходы подчиняются действующему и в данном случае правилу отбора: возможны лишь такие переходы, при которых момент атома изменяется на единицу:

Из всего сказанного выше становится ясным происхождение символов 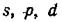и т. д. Будучи заимствованы из названий спектральных серий, эти буквы послужили вначале для обозначения рядов термов, а затем были перенесены на состояния с соответствующими значениями L или /.

17. Магнитный и механический моменты электронов. Спин. Опыты Штерна и Герлаха.

Электрон в атоме движется вокруг ядра. В классической физике движению точки по окружности соответствует момент импульса L=mvr, где m– масса частицы, v – её скорость, r – радиус траектории. В квантовой механике эта формула неприменима, так как неопределенны одновременно радиус и скорость (см. "Соотношение неопределенностей"). Но сама величина момента импульса существует. Как его определить? Из квантово-механической теории атома водорода следует, что модуль момента импульса электрона может принимать следующие дискретные значения:

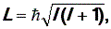(40)

где l – так называемое орбитальное квантовое число, l = 0, 1, 2, … n-1. Таким образом, момент импульса электрона, как и энергия, квантуется, т.е. принимает дискретные значения. Заметим, что при больших значениях квантового числа l (l >>1) уравнение (40) примет вид 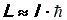. Это не что иное, как один из постулатов Н. Бора.

Из квантово-механической теории атома водорода следует еще один важный вывод: проекция момента импульса электрона на какое-либо заданное направление в пространстве z(например, на направление силовых линий магнитного или электрического поля) также квантуется по правилу:

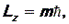(41)

где m= 0, ± 1, ± 2, …± l – так называемое магнитное квантовое число.

Электрон, движущийся вокруг ядра, представляет собой элементарный круговой электрический ток. Такому току соответствует магнитный момент p_m . Очевидно, что он пропорционален механическому моменту импульса L. Отношение магнитного момента p_m электрона к механическому моменту импульса L называется гиромагнитным отношением. Для электрона в атоме водорода

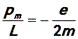(42)

(знак минус показывает, что вектора магнитного и механического моментов направлены в противоположные стороны). Отсюда можно найти так называемый орбитальный магнитный момент электрона:

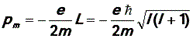(43)

Эта величина,как видим, также квантуется.

В формуле (43) величина 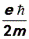является константой. Обозначим её _ви назовем магнетоном Бора. Магнетон Бора служит естественной единицей магнитного момента электрона, так как значения магнитного момента кратны величине _в:

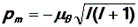(44)

Спин (от англ. spin — вертеть[-ся], вращение) — собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы.

Спин измеряется в единицах 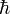(приведённой постоянной Планка, или постоянной Дирака) и равен 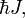где J — характерное для каждого сорта частиц целое (в том числе нулевое) или полуцелое положительное число — так называемое спиновое квантовое число, которое обычно называют просто спином (одно из квантовых чисел).

В связи с этим говорят о целом или полуцелом спине частицы.

Существование спина в системе тождественных взаимодействующих частиц является причиной нового квантовомеханического явления, не имеющего аналогии в классической механике: обменного взаимодействия.

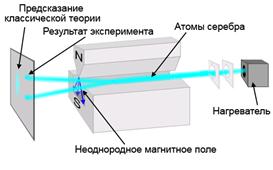
Опыт Штерна — Герлаха — опыт немецких физиков Отто Штерна и Вальтера Герлаха, осуществлённый в 1922 году. Опыт подтвердил наличие у атомов спина (изначально в эксперименте участвовали атомы серебра, а потом и других металлов) и факт пространственного квантования направления их магнитных моментов.

Опыт состоял в следующем: пучок атомов серебра пропускали через сильно неоднородное магнитное поле, создаваемое мощным постоянным магнитом. При прохождении атомов через это поле, в силу обладания ими магнитных моментов, на них действовала зависящая от проекции спина на направление магнитного поля сила, отклонявшая летящие между магнитами атомы от их первоначального направления движения. Причём, если предположить, что магнитные моменты атомов ориентированы хаотично (непрерывно), то тогда на расположенной далее по направлению движения атомов пластинке должна была проявиться размытая полоса. Однако вместо этого на пластинке образовались две достаточно чёткие узкие полосы, что свидетельствовало в пользу того, что магнитные моменты атомов вдоль выделенного направления принимали лишь два определённых значения, что подтверждало предположение квантово-механической теории о квантовании магнитного момента атомов.

Позднее с аналогичными результатами были проделаны опыты для пучков атомов других металлов, а также пучков протонов иэлектронов. Эти опыты доказали существование магнитного момента у рассмотренных частиц и показали их квантовую природу, явив собой доказательство постулатов квантовой теории.

18. Результирующий механический момент многоэлектронного атома. J-J и L-S связь.

Каждый электрон в атоме обладает орбитальным моментом импульса Mi и собственным моментом M_s. Механические моменты связаны с соответствующими магнитными моментами, вследствие чего между всеми Mi и М_в имеется взаимодействие.

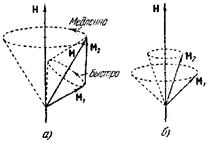
Рис. 210.

Моменты Mi и M_s складываются в результирующий момент атома Mj. При этом возможны два случая.

1. Моменты Mi взаимодействуют между собой сильнее, чем с M_s, которые в свою очередь сильнее связаны друг с другом, чем с Л^. Вследствие этого все M_t складываются в результирующую M_L, a M_s складываются в M_s, а затем ужеM_L и M_s дают результирующую Mj. Такой вид связи встречается чаще всего и называется связью Рессель — Саундерса.

2. Каждая пара Mi и M_s взаимодействует между собой сильнее, чем с другими Mi и М_а, вследствие чего образуются результирующие Mj для каждого электрона в отдельности, которые затем уже объединяются в Mj атома. Такой вид связи, называемый (/, /) -с в я з ь ю, наблюдается у тяжелых атомов.

Сложение моментов осуществляется по квантовым законам [см. (70.2)]. Поясним сказанное несколькими примерами/относящимися к случаю связи Рессель — Саундерса.

1. Два орбитальных момента, определяемых числами 1\ = 2 и /г = 1, могут быть сложены тремя способами и могут дать результирующий момент, соответствующий

значениям квантового числа L> равным 3, 2 и 1. Условно такое сложение можно изобразить векторной схемой, приведенной на рис. 211.

2. При сложении спиновых моментов M_s квантовое число 5 результирующего спинового¹) момента атома Ms может быть целым или полуцелым в зависимости от того, каким будет число электронов в атоме — четным или нечетным.

При четном числе электронов N квантовое число 5 принимает все целые значения от N*^l/₂ (все М₈ «парал-

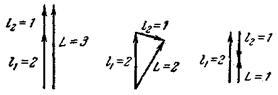
Рис. 211.

лельны» друг другу) до нуля (все M_s попарно компенсируют друг друга). Так, например, при N = 4 (рис. 212, a) S может иметь значения 2, 1, 0.

При нечетном N квантовое число S принимает все полуцелые значения от 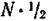(все M_s «йараллельны»

друг другу) до 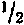(все M_s, кроме одного, попарно компенсируют друг друга). Например, при ЛГ= 5 возможными значениями S будут: 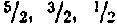(рис. 212,6).

Следовательно, / будет целым, если 5 — целое (т. е. при четном числе электронов в атоме), и полуцелым, если 5 — полуцелое (т. е. при нечетном числе электронов). Так, например:

1) в случае 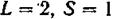возможные значения / равны 3, 2, 1, (рис. 213, а);

2) в случае 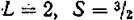возможные значения / равны 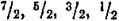(рис. 213, б).

Энергия атома зависит от взаимной ориентации моментов Mi (т. е. от квантового числа L), от взаимной ориентации моментов M_s (от квантового числа. 5) и от взаимной ориентации M_L и M_s (от квантового числа /). Условно терм атома записывается следующим образом:

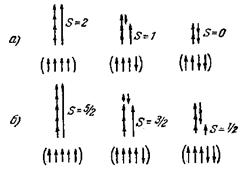
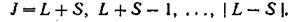
3. При" сложении M_L и M_s квантовое число / результирующего момента Mj может иметь одно из следующих значений:

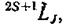(74.1)

где под L подразумевается одна из букв S, P_t D, F и т. д. в зависимости от значения числа L. Например, термы

в случае, если S <L\ когда S > L, число подуровней ровно 2L + 1).

Обозначениями типа (74.1) мы уже пользовались в § 72 применительно к атомам щелочных металлов. Однако для этих элементов характерно то, что S атома, совпадая с s оптического электрона, равно 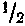. Теперь же мы познакомились с символическими обозначениями термов для любых случаев.