Закон Ома для проводника. Сопротивление проводника. Экспериментальное определение удельного сопротивления проводника. (по лабе 2 стр. 6 всё по лабе).

Закон Ома для проводника-сила тока прямопропорциональна напряжению и обратоно пропорциональна сопротивлению. Y=U/R

Сопротивление проводников

Поступательное движение электронов, дрейфующих по металлическому проводнику, тормозится вследствие столкновения их с ионами атомов проводника. Частота столкновений зависит от структуры материала и его температуры. Возникающее при этом противодействие проводника направленному движению электронов (электрическому току), называется электрическим со противлением проводника и обозначается буквой R (или r ).

Сопротивление проводника зависит от удельного сопротивления мате риала, из которого он изготовлен.

Удельным сопротивлением называется сопротивление проводника длиной 1 м и поперечным сечением 1 мм", с увеличением температуры удельное сопротивление металлов возрастает. Величина сопротивления проводника при заданном его удельном сопротивлении и температуре тем больше, чем больше его длина и тем меньше, чем больше его поперечное сечение.

Из металлов, используемых для проводов электропроводки, медь имеет наименьшее значение удельного сопротивления, но, из-за ее дефицитнос ти, в этих целях более широко используется алюминий. Кроме того, благодаря малой, в сравнении с медью, плотности алюминия, сопротивле ние его, приходящееся на единицу массы, оказывается даже меньше, чем у нее. Правда, существенным недостатком по сравнению с медью, есть невысокая механическая прочность алюминия.

Вынужденные электрические колебания в колебательном контуре.(лаба номер 5 стр. 22 чисто всё по лабе)

Электрический колебательный контур. Экспериментальное изучение собственных затухающих колебаний в колебательном контуре. измерение логарифмического декремента затухания и добротности контура(лаба 4 стр. 17 чисто всё по лабе)

Логарифмический декремент затухания - безразмерная характеристика затухающих колебаний, измеряемая натуральным логарифмом отношения двух последовательных максимальных отклонений колеблющейся величины в одну и ту же сторону.

Вопрос 29

Теорема Гаусса для магнитной индукции

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

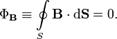
Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является вихревым.

Применение теоремы Гаусса

Для вычисления электромагнитных полей используются следующие величины:

Объёмная плотность заряда (см. выше).

Поверхностная плотность заряда

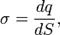
где dS — бесконечно малый участок поверхности.

Линейная плотность заряда

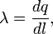
где dl — длина бесконечно малого отрезка.

Теорема о циркуляции магнитного поля — одна из фундаментальных теорем классической электродинамики, сформулированная Андре Мари Ампером в 1826 году. В 1861 году Джеймс Максвелл снова вывел эту теорему, опираясь на аналогии с гидродинамикой. В математической форме входит в число уравнений Максвелла. Теорема гласит:

Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

Математическая формулировка

В математической формулировке теорема имеет следующий вид:

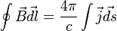
Здесь B — вектор магнитной индукции, j — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме:

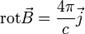
Эквивалентность интегральной и дифференциальной форм следует из теоремы Стокса.

Приведённая выше форма справедлива для вакуума. В веществе часто удобно из полного тока выделить ток намагничения, выразив его через величину намагниченности I и введя вектор напряжённости магнитного поля

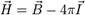
Тогда теорема о циркуляции запишется в форме

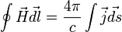
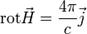
Практическое значение

Теорема о циркуляции играет в магнитостатике приблизительно ту же роль, что и теорема Гаусса в электростатике. В частности, при наличии определённой симметрии задачи, она позволяет просто находить величину магнитного поля во всём пространстве по заданным токам. Например, для вычисления магнитного поля от бесконечного прямолинейного проводника с током по закону Био — Савара — Лапласа потребуется вычислить неочевидный интеграл, в то время как теорема о циркуляции (с учётом осевой симметрии задачи) позволяет дать мгновенный ответ: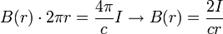

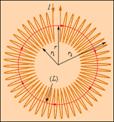
Применение теоремы о циркуляции к тороидальной катушке.

Предполагается, что катушка плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник. В такой катушке линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r1 ≤ r < r2 изображена на рис. 4.17.3. Применим теорему о циркуляции к контуру L в виде окружности, совпадающей с изображенной на рис. 4.17.3 линией индукции магнитного поля. Из соображений симметрии ясно, что модуль вектора одинаков вдоль всей этой линии. По теореме о циркуляции можно записать:B ∙ 2πr = μ0IN,

где N – полное число витков, а I – ток, текущий по виткам катушки. Следовательно,

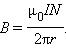
Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, то есть r2 – r1 << r, то магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае B = μ0In.

В это выражение не входит радиус тора, поэтому оно справедливо и в предельном случае r → ∞. Но в пределе каждую часть тороидальной катушки можно рассматривать как длинную прямолинейную катушку. Такие катушки называют соленоидами. Вдали от торцов соленоида модуль магнитной индукции выражается тем же соотношением, что и в случае тороидальной катушки. На рис. 4.17.4 изображено магнитное поле катушки конечной длины. Следует обратить внимание на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. На это указывает густота линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри соленоида.

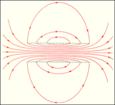
Применение теоремы о циркуляции к расчету магнитного поля бесконечно длинного соленоида.

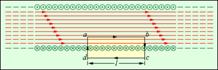
Вектор магнитной индукции имеет отличную от нуля проекцию на направление обхода контура abcd только на стороне ab. Следовательно, циркуляция вектора по контуру равна Bl, где l – длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n · l, где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен Inl. Согласно теореме о циркуляции,Bl = μ0Inl,

откуда B = μ0In.

Это выражение совпадает с полученной ранее формулой для магнитного поля тонкой тороидальной катушки

Вопрос 30

Силовые линии электрического поля.

Силовые линии электрического поля - воображаемые линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности электрического поля в этой точке.

Силовые линии электрического поля начинаются на положительных и заканчиваются на отрицательных зарядах.

Силовые линии электрического поля не пересекаются.

Теорема Гаусса для напряжённости электрического поля в вакууме (электростатическая теорема Гаусса)

Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

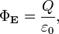
где

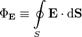— поток вектора напряжённости электрического поля через замкнутую поверхность S.

Q — полный заряд, содержащийся в объёме, который ограничивает поверхность S.

— электрическая постоянная.

Данное выражение представляет собой теорему Гаусса в интегральной форме.

В дифференциальной форме теорема Гаусса выражается следующим образом: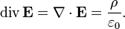

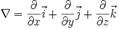
Здесь ρ — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а — оператор набла.

Для теоремы Гаусса справедлив принцип суперпозиции, то есть поток вектора напряжённости через поверхность не зависит от распределения заряда внутри поверхности.

Физической основой теоремы Гаусса является закон Кулона или, иначе, теорема Гаусса является интегральной формулировкой закона Кулона.

Теорема Гаусса для электрической индукции (электрическое смещение)

Для поля в веществе электростатическая теорема Гаусса может быть записана иначе — через поток вектора электрического смещения (электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду: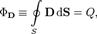

Если же рассматривать теорему для напряжённости поля в веществе, то в качестве заряда необходимо брать сумму свободного заряда, находящегося внутри поверхности и поляризационного (индуцированного, связанного) заряда диэлектрика:

QΣ = Q + Qb,

где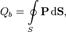

— вектор поляризации диэлектрика.

1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.

Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность 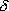заряда в любой точке сферы будет одинакова.

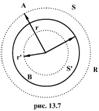
Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен

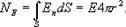
По теореме Гаусса

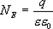
Следовательно

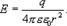
Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.

Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать

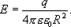
Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г<R. Внутри сферы S зарядов нет, т.к. все они расположены на внешней сферической поверхности, т.е. 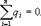Следовательно, по теореме Гаусса, 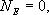и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю. Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис

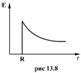
2. Электростатическое поле шара.

Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью .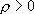

В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда 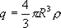, расположенного в центре шара. Тогда вне шара (13.10)

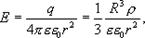
а на его поверхности (r=R) (13.11)

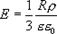
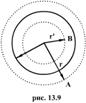
В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом 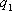, заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен

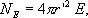
с другой стороны, в соответствии с теоремой Гаусса

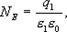
Из сопоставления последних выражений следует (13.12)

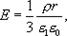
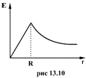
где 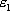- диэлектрическая проницаемость внутри шара. Зависимость напряженности поля, создаваемого заряженной сферой, от расстояния до центра шара приведена на (рис.13.10)

Вопрос 31.

Электрическое поле в диэлектриках

Тело, обладающее электрическим зарядом, создает в окружающем пространстве электрическое поле, которое может быть обнаружено по его воздействию на другие заряженные тела.

Электрическое поле является формой материи. Сила, действующая в электрическом поле на заряженное тело, пропорциональна величине его заряда и зависит от интенсивности самого поля.

Отношение этой силы к величине заряда называется напряженностью поля (Е). В практической системе единиц напряженность поля точечного заряда

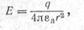
где εа — коэффициент, характеризующий среду, в которой происходит взаимодействие.

Коэффициент εа называют абсолютной диэлектрической проницаемостью; для вакуума в СИ εа = 8,86-10-12 ф/м; эту величину обозначают через ε0 и называют электрической постоянной. Отношение εа, данного вещества к ε0 называется относительной диэлектрической проницаемостью ε'.

Напряженность электрического поля в диэлектрике, при которой происходит пробой, называют электрической прочностью диэлектрика (Епр).

Поляризация диэлектрика - смещение положительных и отрицательных связанных зарядов в макрообъеме диэлектрика в противоположные стороны, что приводит к появлению поверхностных связанных зарядов.

Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента.

Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика

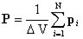
где N - число молекул в объеме 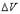. Поляризованность P часто называют поляризацией, понимая под этим количественную меру этого процесса.

В диэлектриках различают следующие типы поляризации: электронную, ориентационную и решеточную (для ионных кристаллов).

Вектор электрического смещения

Если электрическое поле имеет место в диэлектрике, то наблюдается поляризация вещества и появляются связанные электрические заряды.

Учитывают поляризацию с помощью вектора поляризации 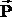, который для анизотропных и однородных сред выражается через напряженность поля следующим образом: 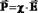, где c – диэлектрическая восприимчивость вещества (диэлектрика). Вектор поляризации равен также поверхностной плотности связанных зарядов, возникающих в диэлектрике под воздействием внешнего электрического поля (Р = sсвяз ).

Кроме этого, при анализе электростатических полей используют вектор электрического смещения:

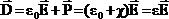
Единицей электрического смещения является кулон на метр квадратный (Кл/м2).

Величина e = e0 + c является основной характеристикой диэлектрика и называется абсолютной диэлектрической проницаемостью. Отношение er = e/e0 называют относительной диэлектрической проницаемостью.

Электрическая поляризуемость 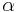определяется как коэффициент пропорциональности между напряжённостью приложенного электрического поля 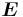и получающимся наведённым электрическим дипольным моментом частицы 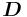в формуле для системы физических единиц СИ:

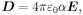
где - 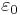электрическая постоянная.

Если моделировать начальную конфигурацию распределения зарядов в виде нейтральной хорошо проводящей тонкостенной пустотелой сферы, либо в виде нейтрального в целом шара, то можно показать, что 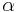равно кубу радиуса этой сферы (шара). Отсюда следует, что размерность 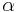есть м3, совпадая с размерностью объёма.

Диэлектрическая проницаемость, величина, характеризующая диэлектрические свойства среды — её реакцию на электрическое поле. В соотношении D = eЕ, где Е — напряжённость электрического поля, D — электрическая индукция в среде, Д. п. — коэффициент пропорциональности e. В большинстве диэлектриков при не очень сильных полях Д. п. не зависит от поля Е. В сильных электрических полях (сравнимых с внутриатомными полями), а в некоторых диэлектриках (например, сегнетоэлектриках) в обычных полях зависимость D от Е — нелинейная.

Величина Д. п. существенно зависит от типа вещества и от внешних условий (температуры, давления и т.п.). В переменных электрических полях Д. п. зависит от частоты поля Е . О методах измерения Д. п. см. Диэлектрические измерения.