Явление самоиндукции. Индуктивность.

Явление самоиндукции - это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.

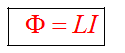
Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.

ЭДС самоиндукции определяется по формуле:

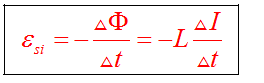
Явление самоиндукции подобно явлению инерции. Так же, как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет явления самоиндукции. Если в цепь, состоящую из двух параллельно подключенных к источнику тока одинаковых ламп, последовательно со второй лампой включить катушку, то при замыкании цепи первая лампа загорается практически сразу, а вторая с заметным запаздыванием.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур[2][3][4].

В формуле

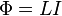
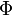— магнитный поток, 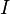— ток в контуре, 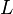— индуктивность.

• Нередко говорят об индуктивности прямого длинного провода (см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведённое выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока[4]:

.

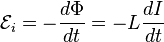Энергия магнитного поля.

Магни́тноепо́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1]; магнитная составляющая электромагнитного поля[2].

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты).

Кроме этого, оно возникает в результате изменения во времени электрического поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции 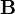(вектор индукции магнитного поля)[3][4]. С математической точки зрения 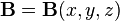— векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).

Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.

Приращение плотности энергии магнитного поля равно:

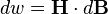
где:

H — напряжённость магнитного поля,

B — магнитная индукция

В линейном тензорном приближении магнитная проницаемость есть тензор (обозначим его 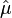) и умножение вектора на неё есть тензорное (матричное) умножение:

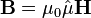или в компонентах[12] .

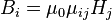Плотность энергии в этом приближении равна:

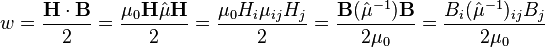
Механические колебания под действием упругой силы. Уравнение гармонических колебаний, амплитуда, частота, период и фаза колебаний, начальная фаза. Колебания координаты и скорости груза, закрепленного на упругой пружине.

В природе и технике, кроме поступательного и вращательного движений, часто встречается еще один вид механического движения - колебания.

Совершают колебания ветви дерева на ветру и маятник в часах, поршень в цилиндре двигателя внутреннего сгорания и земная кора во время землетрясений, струна гитары и поверхностный слой воды на море. Общий признак колебательного движения во всех этих примерах - точное или приблизительное повторение движения через одинаковые промежутки времени. Механическими колебаниями называют движения тел, повторяющиеся точно или приблизительно через одинаковые промежутки времени.

Свободные и вынужденные колебания. Силы, действующие между телами внутри рассматриваемой системы тел, называют внутренними силами. Силы, действующие на тела системы со стороны других тел, не входящих в эту систему, называют внешними силами.

График этой функции дает наглядное представление о протекании процесса колебаний во времени. Получить такой график можно построением по точкам графика функции 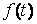в координатных осях 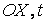(рис. 215).

Рис. 215

Период и частота колебаний. Общим признаком механических колебаний как физического процесса является повторяемость процесса движения через определенный промежуток времени. Миндальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний. Период колебаний (обозначается буквой 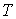) выражается в секундах.

Физическая величина, обратная периоду колебаний, называется частотой колебаний:

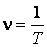(59.1)

Частота определяет число колебаний, происходящих за 1 с. Единица частоты - герц (Гц). 1 Гц = 1 с^-1. В физике и технике широко используется понятие циклической частоты. Циклическая частота определяет число колебаний, происходящих за 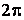с. Связь между циклической частотой 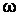и частотой 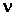задается выражением

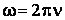. (69.2)

Циклическая частота 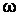и период колебаний 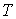связаны соотношением

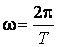. (59.3)

Гармонические колебания. Гармоническими колебаниями называют колебания, описываемые уравнением

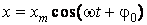. (60.1)

Здесь 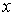- смещение тела от положения равновесия, 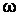- циклическая частота колебаний, 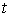- время.

Амплитуда и фаза колебаний. Модуль максимального смещения 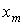тела от положения равновесия называется амплитудой колебаний. Величина, стоящая под знаком косинуса, называется фазой 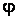гармонического колебания:

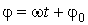. (60.2)

Фаза колебаний 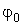в начальный момент времени 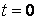называется начальной фазой.

Скорость и ускорение при гармонических колебаниях. Найдем, как зависят от времени скорость и ускорение тела, совершающего гармонические колебания по закону

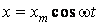(60.3)

вдоль координатной оси ОХ . Скорость 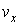движения тела определяется выражением

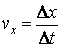
Более строго проекция скорости поступательного движения тела на ось ОХ определяется как производная координаты 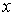по времени:

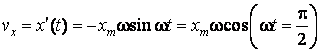(60.4)

Для определения проекции ускорения движения тела в любой момент времени необходимо найти производную от проекции скорости 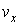по времени :

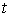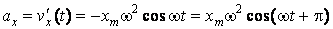(60.5)

Гармонические колебания под действием силы упругости. Из уравнений (60.3) и (60.5) следует, что

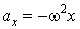. (60.6)

При гармонических колебаниях тела вдоль оси ОХ ускорение прямо пропорционально смещению 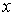тела от положения равновесия.

Примером силы, пропорциональной смещению тела, является сила упругости. По закону Гука сила упругости прямо пропорциональна деформации 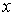тела:

.

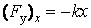Действие силы упругости может вызывать возникновение гармонических колебаний. Примером гармонических колебаний, возникающих под действием силы упругости, могут служить колебания груза, подвешенного на стальной пружине, колебания струны.

Если тело массой 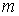совершает под действием силы упругости гармонические колебания с циклической частотой 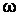, то, применив второй закон Ньютона для проекции ускорения 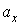, получим

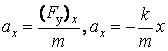(60.7)

С другой стороны, ускорение при гармонических колебаниях с циклической частотой 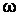определяется в любой момент времени выражением (60.6). Из выражений (60.6) и (60.7) устанавливается связь между циклической частотой 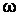, жесткостью 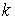деформируемого тела и массой 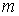тела:

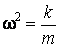(60.8)