Электростатическое поле и его основные характеристики. Напряженность поля. Принцип суперпозиции полей.

Потенциал электростатического поля. Принцип суперпозиции для потенциала.

Скалярная физическая величина, введенная для количественного оценивания способности поля перемещать заряженные частицы и равная отношению энергии W , характеризующей изменение состояния положительно заряженной частицы при ее перемещении из данной точки в бесконечно удаленную, к заряду q этой частицы:φ= W/q.

Для потенциалов относительно слабых электростатических полей выполняется принцип суперпозиции. Если электростатическое поле создаётся системой неподвижных электрических зарядов , ,…, и поле каждого заряда в отсутствие других зарядов описывается некоторым потенциалом, то потенциал суммарного поля всей системы зарядов есть сумма потенциалов полей всех зарядов системы по отдельности

,

Диполь в электростатическом поле.

Электрическим диполем называется система двух одинаковых по величине, но разноименных точечных зарядов, расстояние между которыми l значительно меньше расстояния до тех точек, в которых определяется поле системы ( ) (рис. 1.6).

Здесь называютплечо диполя – вектор, направленный от отрицательного заряда к положительному и численно равный расстоянию между зарядами.

Рис. 1.6

Пример 1. Найдем Е^ в точке А на прямой, проходящей через центр диполя и перпендикулярной к оси (рис. 1.6)

(т.к. )

(1.5.1)

Полярные диэлектрики.

Молекулы полярных диэлектриков с точки зрения электрических свойств являются диполями, вот как то так.

Например, молекула NaCl или воды.

При отсутствии внешнего электрического поля молекулы-диполи полярного диэлектрика, совершая хаотическое тепловое движение, ориентированы в самых разных направлениях. Электрические поля этих диполей полностью компенсируют друг друга, и результирующее поле равно нулю во всех областях диэлектрика. Но если поместить такой диэлектрик во внешнее поле E₀, то оно «развернёт» диполи так, что они окажутся ориентированными вдоль линий напряжённости («минусы» диполей повернутся влево — к тем «плюсам», которые создают внешнее поле).

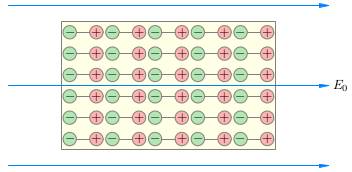
Неполярные диэлектрики.

Диэлектрик называется неполярным, если его молекулы имеют симметричное распределение положительных и отрицательных зарядов, и потому не ведут себя как диполи. К неполярным диэлектрикам относятся, например, керосин, масло, воздух, инертные газы. Тем не менее, поляризация наблюдается и у неполярных диэлектриков.

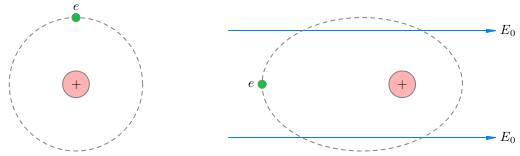
Слева изображена симметричная электронная орбита в атоме неполярного диэлектрика. При наложении внешнего поля E₀ эта орбита деформируется (справа): электрон смещается в сторону положительных зарядов, создающих внешнее поле. Мы видим, что во внешнем поле электрон будет проводить больше времени слева от ядра, нежели чем справа. Из-за этого центры положительных и отрицательных зарядов в атоме неполярного диэлектрика разойдутся в разные стороны. То есть получаем какбэ диполь, но не диполь.

Электронная поляризация присутствует и у полярных диэлектриков; но там она теряется на фоне куда более мощного эффекта разворота самих диполей.

Вектор магнитной индукции.

Электрический ток оказывает магнитное действие Таким образом, магнитное поле порождается движущимися зарядами.

Вектор магнитной индукции— векторная физическая величина, направление которой в данной точке совпадает с направлением, указываемым в этой точке северным полюсом свободной магнитной стрелки.

Модуль вектора магнитной индукции— физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины отрезка проводника:

Электрический ток оказывает магнитное действие Таким образом, магнитное поле порождается движущимися зарядами.

Вектор магнитной индукции— векторная физическая величина, направление которой в данной точке совпадает с направлением, указываемым в этой точке северным полюсом свободной магнитной стрелки.

Модуль вектора магнитной индукции— физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины отрезка проводника:

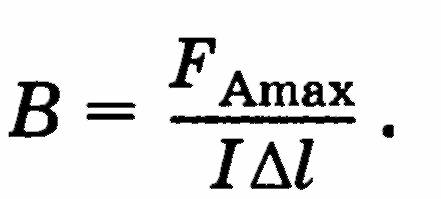Единица магнитной индукции — тесла (1 Тл).

Круговой проводник с током.

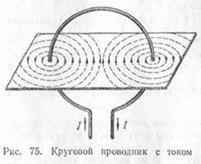
Возьмем проводник, согнутый по кругу в виде витка, и пропустим по нему ток (рис. 75). Из чертежа видно, что магнитные линии замыкаются вокруг проводника с током и имеют форму ок­ружностей. Магнитные линии с одной стороны входят в плоскость кругового проводника, с другой — выходят.

Направление поля круго­вого тока можно определить, пользуясь «правилом бурав­чика».

Буравчик нужно расположить по оси кругового тока перпендикулярно его плоскости. Если теперь вращать ручку буравчика по направлению тока в контуре, то поступательное движение буравчика покажет направление магнит­ного поля. Напряженность магнитного поля в центре витка с током определяется по формуле:

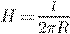
Энергия магнитного поля.

Магни́тноепо́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1]; магнитная составляющая электромагнитного поля[2].

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты).

Кроме этого, оно возникает в результате изменения во времени электрического поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции 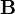(вектор индукции магнитного поля)[3][4]. С математической точки зрения 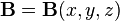— векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).

Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.

Приращение плотности энергии магнитного поля равно:

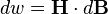
где:

H — напряжённость магнитного поля,

B — магнитная индукция

В линейном тензорном приближении магнитная проницаемость есть тензор (обозначим его 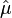) и умножение вектора на неё есть тензорное (матричное) умножение:

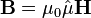или в компонентах[12] .

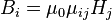Плотность энергии в этом приближении равна:

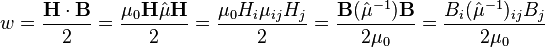
Механические колебания под действием упругой силы. Уравнение гармонических колебаний, амплитуда, частота, период и фаза колебаний, начальная фаза. Колебания координаты и скорости груза, закрепленного на упругой пружине.

В природе и технике, кроме поступательного и вращательного движений, часто встречается еще один вид механического движения - колебания.

Совершают колебания ветви дерева на ветру и маятник в часах, поршень в цилиндре двигателя внутреннего сгорания и земная кора во время землетрясений, струна гитары и поверхностный слой воды на море. Общий признак колебательного движения во всех этих примерах - точное или приблизительное повторение движения через одинаковые промежутки времени. Механическими колебаниями называют движения тел, повторяющиеся точно или приблизительно через одинаковые промежутки времени.

Свободные и вынужденные колебания. Силы, действующие между телами внутри рассматриваемой системы тел, называют внутренними силами. Силы, действующие на тела системы со стороны других тел, не входящих в эту систему, называют внешними силами.

График этой функции дает наглядное представление о протекании процесса колебаний во времени. Получить такой график можно построением по точкам графика функции 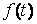в координатных осях 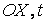(рис. 215).

Рис. 215

Период и частота колебаний. Общим признаком механических колебаний как физического процесса является повторяемость процесса движения через определенный промежуток времени. Миндальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний. Период колебаний (обозначается буквой 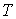) выражается в секундах.

Физическая величина, обратная периоду колебаний, называется частотой колебаний:

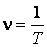(59.1)

Частота определяет число колебаний, происходящих за 1 с. Единица частоты - герц (Гц). 1 Гц = 1 с^-1. В физике и технике широко используется понятие циклической частоты. Циклическая частота определяет число колебаний, происходящих за 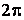с. Связь между циклической частотой 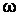и частотой 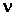задается выражением

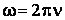. (69.2)

Циклическая частота 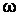и период колебаний 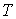связаны соотношением

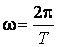. (59.3)

Гармонические колебания. Гармоническими колебаниями называют колебания, описываемые уравнением

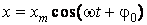. (60.1)

Здесь 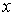- смещение тела от положения равновесия, 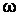- циклическая частота колебаний, 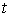- время.

Амплитуда и фаза колебаний. Модуль максимального смещения 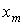тела от положения равновесия называется амплитудой колебаний. Величина, стоящая под знаком косинуса, называется фазой 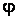гармонического колебания:

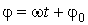. (60.2)

Фаза колебаний 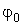в начальный момент времени 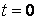называется начальной фазой.

Скорость и ускорение при гармонических колебаниях. Найдем, как зависят от времени скорость и ускорение тела, совершающего гармонические колебания по закону

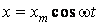(60.3)

вдоль координатной оси ОХ . Скорость 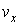движения тела определяется выражением

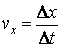
Более строго проекция скорости поступательного движения тела на ось ОХ определяется как производная координаты 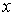по времени:

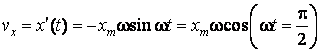(60.4)

Для определения проекции ускорения движения тела в любой момент времени необходимо найти производную от проекции скорости 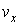по времени :

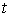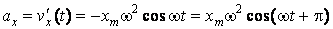(60.5)

Гармонические колебания под действием силы упругости. Из уравнений (60.3) и (60.5) следует, что

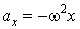. (60.6)

При гармонических колебаниях тела вдоль оси ОХ ускорение прямо пропорционально смещению 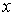тела от положения равновесия.

Примером силы, пропорциональной смещению тела, является сила упругости. По закону Гука сила упругости прямо пропорциональна деформации 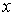тела:

.

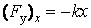Действие силы упругости может вызывать возникновение гармонических колебаний. Примером гармонических колебаний, возникающих под действием силы упругости, могут служить колебания груза, подвешенного на стальной пружине, колебания струны.

Если тело массой 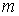совершает под действием силы упругости гармонические колебания с циклической частотой 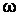, то, применив второй закон Ньютона для проекции ускорения 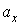, получим

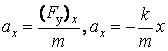(60.7)

С другой стороны, ускорение при гармонических колебаниях с циклической частотой 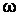определяется в любой момент времени выражением (60.6). Из выражений (60.6) и (60.7) устанавливается связь между циклической частотой 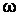, жесткостью 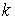деформируемого тела и массой 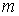тела:

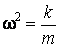(60.8)

Электростатическое поле и его основные характеристики. Напряженность поля. Принцип суперпозиции полей.

Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга[1].

Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный точечный заряд, помещённый в это поле. Пробный заряд должен быть ничтожно малым, чтобы не повлиять на характеристику электростатического поля.

Электрическое поле называют однородным, если вектор его напряженности одинаков во всех точках поля.

Основные характеристики электростатического поля:

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный точечный заряд, помещенный в данную точку поля, к величине этого заряда :

.

Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл (подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Принцип суперпозиции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:

• результат воздействия на частицу нескольких внешних сил есть просто сумма результатов воздействия каждой из сил.

Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что электростатический потенциал, создаваемый в данной точке системой зарядов, есть сумма потенциалов отдельных зарядов.

Принцип суперпозиции может принимать и иные формулировки, которые, подчеркнём, полностью эквивалентны приведённой выше:

• Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя;
• Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.
• Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.

Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.

Принцип суперпозиции является следствием, прямо вытекающим из рассматриваемой теории, а вовсе не постулатом, вносимым в теорию априори. Так, например, в электростатике принцип суперпозиции есть следствие того факта, что уравнения Максвелла в вакууме линейны. Именно из этого следует, что потенциальную энергию электростатического взаимодействия системы зарядов можно легко сосчитать, вычислив потенциальную энергию каждой пары зарядов.