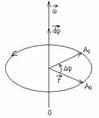
Движение точки по окружности. Угловые перемещение, ускорение, скорость. Связь между линейными и угловыми характеристиками.
Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением.
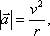 где r – радиус окружности.
где r – радиус окружности.
Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.
Кроме центростремительного ускорения, важнейшими характеристиками равномерного движения по окружности являются период и частота обращения.
Вращательное движение тела или точки характеризуется углом поворота, угловой скоростью и угловым ускорением.
Угол поворота φ - это угол между двумя последовательными положениями радиуса вектора r, соединяющего тело или материальную точку с осью вращения. Угловое перемещение измеряется в радианах.
Угловая скорость (w) – векторная физическая величина, показывающая, как изменяется угол поворота в единицу времени и численно равная первой производной от угла поворота по времени, т.е
. 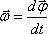
Направление вектора угловой скорости 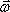 совпадает с направлением вектора углового перемещения, т.е. вектора, численно равного углу φ и параллельного оси вращения; оно определяется по правилу буравчика: если совместить ось буравчика с осью вращения и поворачивать его в сторону движения вращающейся точки, то направление поступательного перемещения буравчика определит направление вектора угловой скорости. Точка приложения вектора произвольна, это может быть любая точка плоскости, в которой лежит траектория движения. Удобно совмещать этот вектор с осью вращения.
совпадает с направлением вектора углового перемещения, т.е. вектора, численно равного углу φ и параллельного оси вращения; оно определяется по правилу буравчика: если совместить ось буравчика с осью вращения и поворачивать его в сторону движения вращающейся точки, то направление поступательного перемещения буравчика определит направление вектора угловой скорости. Точка приложения вектора произвольна, это может быть любая точка плоскости, в которой лежит траектория движения. Удобно совмещать этот вектор с осью вращения.
При равномерном вращении численное значение угловой скорости не меняется, т.е. ω = const. Равномерное вращение характеризуется:
- периодом вращения Т, т.е. временем, за которое тело делает один полный оборот, период обращения измеряется в с;
- частотой, измеряемой в Гц и показывающей число оборотов в с;
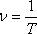
- круговой (циклической,угловой) частотой (это та же самая угловая скорость).
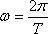
Угловая скорость может меняться как по величине, так и по направлению. Векторная величина, характеризующая изменение угловой скорости в единицу времени и численно равная второй производной от углового перемещения по времени, называется угловым ускорением:
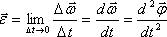
Если положение и радиус окружности, по которой происходит вращение не изменяется со временем, то направление векторов углового ускорения и угловой скорости совпадают, если вращение ускоренное, и противоположны, если вращение замедленное.
При равномерном движении по окружности тангенциальная составляющая ускорения равна нулю, т.е. модуль линейной скорости постоянен и определяется соотношением 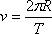 Но т.к. направление скорости постоянно изменяется, то существует нормальное ускорение
Но т.к. направление скорости постоянно изменяется, то существует нормальное ускорение 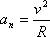 Т.о., линейная скорость
Т.о., линейная скорость 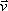 направлена по касательной к окружности в каждой точке по движению; ускорение
направлена по касательной к окружности в каждой точке по движению; ускорение 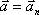 перпендикулярно скорости и направлено к центру кривизны.
перпендикулярно скорости и направлено к центру кривизны.