Теорема о движении центра масс системы

Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил

ma=(сумма F)

5) Виды сил в механике. 4 Вида взаимодействия в природе. Центр масс системы точек.

Виды сил в механике:

1) Сила тяжести:

Одно из проявлений силы всемирного тяготения - сила тяжести, то есть сила притяжения тел к Земле. Обозначим массу Земли М, ее радиус R, массу данного тела m, тогда сила, действующая на тело вблизи поверхности Земли, согласно закону всемирного тяготения будет равна:

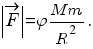
Это и есть сила тяжести. Направлена она к центру Земли.
Если на тело действует только эта сила (а все другие уравновешены), то оно совершает свободное падение. Ускорение этого свободного падения можно найти, применив второй закон Ньютона,

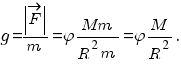
Отсюда видно, что ускорение свободного падения g не зависит от массы m тела и, следовательно, оно одинаково для всех тел. Теперь можно написать, что сила тяжести

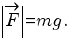
сила тяжести, а значит, и ускорение свободного падения изменяются при удалении от поверхности Земли. Если тело находится на высоте h над поверхностью Земли, то выражение для ускорения свободного падения нужно писать в виде

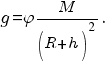
На экваторе же система отсчета (та же линейка) движется с ускорением 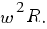Ускорение g тела относительно неподвижной системы отсчета равно сумме двух ускорений: ускорения g' тела относительно движущейся системы отсчета и ускорения 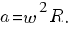движущейся системы относительно неподвижной. Следовательно,

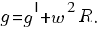
Отсюда ускорение, измеренное на экваторе, равно:

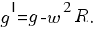
Оно меньше, чем на полюсах, на величину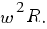

2) Сила упругости:

Си́лаупру́гости — сила, возникающая при деформации тела и противодействующая этой деформации.

В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. В простейшем случае растяжения/сжатия тела сила упругости направлена противоположно смещению частиц тела, перпендикулярно поверхности.

Вектор силы противоположен направлению деформации тела (смещению его молекул).

Зако́нГу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёнымРобертом Гуком (Хуком) (англ. RobertHooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.

В словесной форме закон звучит следующим образом:

Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена противоположно направлению перемещения частиц тела относительно других частиц при деформации.

,

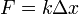где 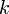— жёсткость тела, 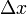— величина деформации .

3) Сила трения:

Обсуждая до сих пор силы, мы не интересовались их происхождением. Однако в меха­нике мы будем рассматривать различные силы: трения, упругости, тяготения.

Из опыта известно, что всякое тело, движущееся по горизонтальной поверхности другого тела, при отсутствии действия на него других сил с течением времени замедля­ет свое движение и в конце концов останавливается. Это можно объяснить существова­нием силы трения, которая препятствует скольжению соприкасающихся тел друг относительно друга. Силы трения зависят от относительных скоростей тел. Силы трения могут быть разной природы, но в результате их действия механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел.

Различают внешнее (сухое) и внутреннее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении. Если соприкасающиеся тела неподвижны друг относительно друга, говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трении скольжения, качения или верчения.

Внутренним трением называется трение между частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых меняются от слоя к слою. В отличие от внешнего трения здесь отсутствует трение покоя. Если тела скользят относительно друг друга и разделены прослойкой вязкой жидкости (смазки), то трение происходит в слое смазки. В таком случае говорят о гидродинамическом трении (слой смазки достаточно толстый) и граничном трении (толщина смазоч­ной прослойки »0,1 мкм и меньше).

Обсудим некоторые закономерности внешнего трения. Это трение обусловлено шероховатостью соприкасающихся поверхностей; в случае же очень гладких поверх­ностей трение обусловлено силами межмолекулярного притяжения.

закон: сила трения скольжения Fтр пропорциональна силе N нормального давления, с которой одно тело действует на другое:

Fтр = f N ,

где f — коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.

Найдем значение коэффициента трения. Если тело находится на наклонной плоско­сти с углом наклона a (рис.12), то оно приходит в движение, только когда тангенциаль­ная составляющая F силы тяжести Р больше силы трения Fтр. Следовательно, в пре­дельном случае (начало скольжения тела) F=Fтр. или Psina0 = f N = f P cosa0, откуда

f = tga0.

Таким образом, коэффициент трения равен тангенсу угла a0, при котором начинается скольжение тела по наклонной плоскости.

Для гладких поверхностей определенную роль начинает играть межмолекулярное притяжение. Для них применяется закон трения скольжения

Fтр = f ист (N + Sp0),

где р0 — добавочное давление, обусловленное силами межмолекулярного притяжения, которые быстро уменьшаются с увеличением расстояния между частицами; S — пло­щадь контакта между телами; fист — истинный коэффициент трения скольжения.

4 вида взаимодействий в природе:

Фундамента́льныевзаимоде́йствия — качественно различающиеся типы взаимодействияэлементарных частиц и составленных из них тел.

На сегодня достоверно известно существование четырех фундаментальных взаимодействий:

А) гравитационного(Гравита́ция (притяжение, всеми́рноетяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — универсальное фундаментальное взаимодействие между всеми материальными телами. В приближении малых скоростей и слабого гравитационного взаимодействия описывается теорией тяготения Ньютона, в общем случае описывается общей теорией относительностиЭйнштейна. Гравитация является самым слабым из четырех типов фундаментальных взаимодействий.)

Б) электромагнитного(Электромагни́тноевзаимоде́йствие — одно из четырёх фундаментальных взаимодействий. Электромагнитное взаимодействие существует между частицами, обладающимиэлектрическим зарядом[1]. С современной точки зрения электромагнитное взаимодействие между заряженными частицами осуществляется не прямо, а только посредством электромагнитного поля.)

В) сильного(Си́льное ядерное взаимоде́йствие (цветово́евзаимоде́йствие, я́дерноевзаимоде́йствие) — одно из четырёх фундаментальных взаимодействий в физике. В сильном взаимодействии участвуют кварки и глюоны и составленные из них частицы, называемые адронами (барионы и мезоны). Оно действует в масштабах порядка размера атомного ядра и менее, отвечая за связь между кварками в адронах и за притяжение между нуклонами (разновидность барионов — протоны и нейтроны) в ядрах.)

Г) слабого(Слабое взаимодействие, или слабое ядерное взаимодействие — одно из четырёх фундаментальных взаимодействий в природе. Оно ответственно, в частности, за бета-распадядра. Это взаимодействие называется слабым, поскольку два других взаимодействия, значимые для ядерной физики (сильное и электромагнитное), характеризуются значительно большей интенсивностью. Однако оно значительно сильнее четвёртого из фундаментальных взаимодействий, гравитационного. Слабое взаимодействие является короткодействующим — оно проявляется на расстояниях, значительно меньших размера атомного ядра )

При этом электромагнитное и слабое взаимодействия являются проявлениями единого электрослабого взаимодействия.

Центр масс системы точек:

Центр масс, центр ине́рции, барице́нтр (от др.-греч. βαρύς — тяжёлый + κέντρον — центр) — (в механике) геометрическая точка, характеризующая движение тела или системы точек как целого.

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

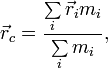
где

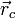— радиус-вектор центра масс,

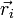— радиус-вектор i-й точки системы,

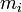— масса i-й точки.

Центр масс, таким образом, характеризует распределение массы по телу или системе точек.

6. Работа, энергия и мощность силы в поступательном и вращательном движениях. Кинетическая энергия и работа сил.

1.Работа и работа сил

Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.Единица работы —джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н × м).

Элементарной работой силы 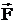называется величина, равная скалярному произведению силы на элементарное перемещение :

,

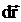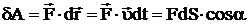где 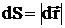– элементарный путь точки приложения силы за время dt, a – угол между векторам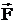и и .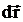

Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом:

.

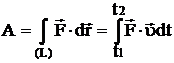Если 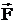= const, то А= × .

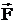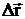При вращательном движении работа определяется проекцией момента сил на направление угловой скорости:

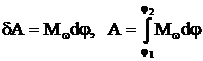
если М_w = const, то А = М_w×j.

2.Мощность.

Быстроту совершения работы характеризует мощность. Мощностью называется скалярная величина, равная работе, совершаемой в единицу времени:

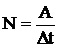– средняя мощность; 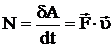– мгновенная мощность.

При вращательном движении мощность определяется следующим образом:

.

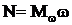2.Энергия.Кинетическая энергия

Энергия— универсальная мера различных форм движения и взаимодействия. С раз­личными формами движения материи связывают различные формы энергии: механи­ческую, тепловую, электромагнитную, ядерную и др.

Энергия также бывает кинетическая и потенциальная, а вместе они составляют полную механическую энергию.

Кинетической энергией тела называется функция механического состояния, зависящая от массы тела и скорости его движения (энергия механического движения).

Кинетическая энергия поступательного движения

.

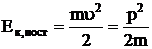Кинетическая энергия вращательного движения

.

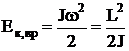При сложном движении твёрдого тела его кинетическая энергия может быть представлена через энергию поступательного и вращательного движения:

.

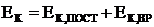7. Консервативные и диссипативные сила. Потенциальное поле. Потенциальная энергия упругой силы. Работа по растяжению и сжатию пружины.

1.Консервативная и Диссипативная сила. Потенциальное поле.

Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил – работа на замкнутой траектории равна нулю:

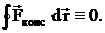
К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.

Неконсервативными(диссипативными) силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.

Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, — консервативными

2.Потенциальная энергия упругой силы и работа по растяжению и сжатию пружины.

Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией ), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к нерастянутому состоянию, т.е. найдем упругую энергию растянутой пружины.

Пусть, например, растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. При нахождении работы мы должны учитывать, что сила , с которой действует пружина, не остается постоянной при изменении растяжения. Мы видели (§ 37), что сила упругости пружины пропорциональна ее растяжению. Если первоначальное растяжение пружины, считая от ее нерастянутого состояния, равнялось l, то первоначальное значение силы упругости составляло F=kl, где k — коэффициент пропорциональности, который называют коэффициентом упругости пружины. По мере сокращения пружины эта сила равномерно убывает от значения kl до нуля.

Значит, среднее значение силы равно Fср=kl. Можно показать, что для вычисления работы А изменяющейся силы упругости нужно это среднее значение силы умножить на перемещение точки приложения силы :

A=1/2 kl•l=1/2kl2.

Таким образом, потенциальная энергия упругости Еп равна

Eп = 1/2 kl2. (98.1)