Растворы. Идеальные растворы. Законы Рауля и Генри. Термодинамическая активность.

Раствором называется однородная, состоящая из 2-х и более веществ система, состав которой может в определенных пределах непрерывно изменяться.

Идеальные растворы – это модели растворов, в которых законы Рауля и Генри выполняются с абсолютной точностью.

Оба закона устанавливают зависимость давления пара компонента над раствором от концентрации этого компонента в растворе.

Первый закон Рауля связывает давление насыщенного пара над раствором с его составом; он формулируется следующим образом:

• Парциальное давление насыщенного пара компонента раствора прямо пропорционально его мольной доле в растворе, причём коэффициент пропорциональности равен давлению насыщенного пара над чистым компонентом.

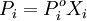
Растворы, для которых выполняется закон Рауля, называются идеальными. Идеальными при любых концентрациях являются растворы, компоненты которых очень близки по физическим и химическим свойствам (оптические изомеры, гомологи и т. п.), и образование которых не сопровождается изменением объёма и выделением либо поглощением теплоты.

Закон Генри: Закон Генри – это положение, согласно которому при постоянной температуре растворимость газа в данной жидкости (выраженная его весовой концентрацией) прямо пропорциональна давлению этого газа над раствором. При этом под растворимостью понимается способность вещества образовывать с другими веществами однородные системы

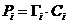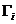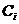-константа (постоянная) Генри зависит от природы компонентов раствора и от выбранных единиц выражения концентраций_.

-концентрация растворенного компонента.Она может быть выражена в любых единицах, в том числе и в % по массе.

Концентрационный интервал, в котором реальные растворы подчиняются закону Генри, колеблется от долей процента до нескольких процентов.

Под активностью компонента в растворе понимают отношение парциального давления пара компонента над раствором к давлению пара этого же вещества, находящегося в стандартном состоянии

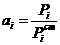Активность имеет тот же физический смысл, что и концентрация, но учитывает взаимодействие частиц в растворе

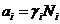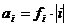Термодинамические параметры взаимодействия, их использование в расчетах.

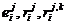Производные уравнения называются массовыми параметрами взаимодействия первого и второго порядков и обозначаются соответственно

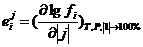
-массовый параметр взаимодействия компонента i с компонентом j первого порядка.

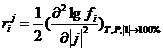
-массовый параметр взаимодействия компонента i с компонентом

j второго порядка

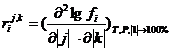
-массовый перекрестный параметр взаимодействия компонента i

второго порядка.

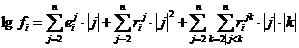
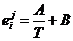Обычно температурная зависимость параметров взаимодействия имеет вид

А и В – компоненты, Т – температура, К.