Идеальный газ. Уравнение состояния. Закон Дальтона. Реальные газы.

Идеальный газ. Уравнение состояния. Закон Дальтона. Реальные газы.

Идеальный газ – газ, молекулы которого рассматриваются как невзаимодействующие друг с другом материальные точки.

Модель идеального газа:

1.Молекулы (атомы)принимаются за материальные точки с определенной массой.Размеры их ничтожны по сравнению с расстоянием между ними.

2.Молекулы(атомы) находятся в состоянии непрерывного и постоянного движения.

Между столкновениями они движутся прямолинейно. Движения равновероятны по всем направлениям.

3.Скорости частиц могут быть любыми.

4.При столкновении молекулы (атомы) ведут себя как упругие шары. Между частицами не действуют силы притяжения или отталкивания

Уравнение состояния(иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

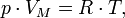
Где

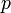— давление,

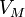— молярный объём,

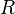— универсальная газовая постоянная

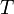— абсолютная температура,К.

Уравнения идеального газа

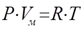
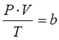
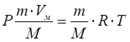
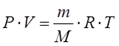
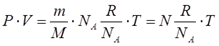
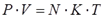
Реальные газы

При повышении плотности изменяются свойства газов – они перестают быть идеальными. Простейшим уравнением, которое качественно правильно описывает отличие реального газа от идеального, является уравнение Ван-дер-Ваальса

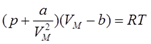
Закон Дальтона

Общее давление смеси идеальных газов равно сумме парциальных давлений компонентов.

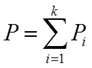
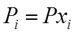, Xi-молярная доля i-го компонента в смеси.

Внутренняя энергия и энтальпия. Первый закон термодинамики.

Внутренняя энергия - характеризует общий запас энергии системы, включает все виды движения и взаимодействия частиц, составляющих систему.

Свойства:

1. Внутренняя энергия не может равняться нулю (нет веществ без движения).

Она всегда положительна и тем больше, чем больше движение.

2.Внутренняя энергия изолированной системы всегда остается постоянной величиной, независимо от протекающих в системе процессов.

3.Внутренняя энергия складывается из отдельных видов энергии, которые превращаются друг в друга в строго эквивалентных количествах.

4.Внутренняя энергия является однозначной функцией состояния системы, т.е. каждому состоянию системы соответствует одно значение внутренней энергии.

Закон термодинамики

Первый закон термодинамики (закон сохранения энергии для тепловых процессов) определяет количественное соотношение между изменением внутренней энергии системы дельта U, количеством теплоты Q, подведенным к ней, и суммарной работой внешних сил A, действующих на систему.

Первый закон термодинамики – изменение внутренней энергии системы при ее переходе из одного состояния в другое равно сумме количества теплоты, подведенного к системе извне, и работы внешних сил, действующих на нее:

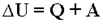
Вечный двигатель первого рода не возможен – таков вывод из первого закона термодинамики.

Энтальпия

Энтальпия— термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц.

Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенных температуре и давлении.

ЭНТАЛЬПИЯ системы (Н) – есть величина, равная сумме внутренней энергии (U) и потенциальной энергии всестороннего сжатия (PV)

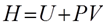
Химическое равновесие. Условия равновесия. Константа равновесия, и ее зависимость от температуры. Примеры записи константы равновесия для реакций с участием газовой и конденсированных фаз.

Химическое равновесие – состояние химической системы, при котором возможны реакции, идущие с равными скоростями в противоположных направлениях. При химическом равновесии концентрации реагентов, температура и другие параметры системы не изменяются со временем.

Условия:

1.Неизменность равновесного состояния системы при сохранении внешних условий.

2. Устойчивость равновесия.

3. Динамический характер равновесия.

Константа равновесия:

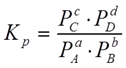
Константа равновесия – есть отношение произведений парциальных давлений продуктов реакции к произведению парциальных давлений исходных веществ, взятых в степенях, равных стехиометрическим коэффициентам реакции.

Зависимость константы равновесия от температуры:

Уравнение, связывающее изменении Крс температурой при Р=const носит название изобары химической реакции.

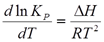
Уравнение показывает, что знак производной определяется знаком теплового эффекта реакции. Если производная положительна, то функция lnKpявляется возрастающей.

Таким образом:

Для эндотермических реакций, для которых ΔH>0, Kp возрастает с ростом температуры.

Для экзотермических реакций, для которых ΔH<0, Kpуменьшается с ростом температуры.

В тех случаях, когда тепловой эффект реакции очень мал (близок к нулю),Кр не зависит от температуры.

Принцип смещения равновесий. Примеры его использования.

Химическим равновесием называется такое состояние химической системы, при котором количества исходных веществ и продуктов не меняются со временем.

Принципом смещения равновесия называют принцип Ле-Шателье.

Формулировка: Равновесие смещается в направлении, обратном оказанному на систему внешнему воздействию.

Применяя принцип ЛеШателье, можно качественно определить влияние температуры и давления на положение равновесия и предсказать, какие условия будут способствовать протеканию процесса в желаемом направлении. Если в процессе образуется большее число газообразных молей веществ, чем вступает в реакцию, то для смещения равновесия вправо необходимо понижать давление в системе. Если процесс идет с уменьшением числа молей газообразных компонентов, то чтобы повысить его эффективность, нужно повысить давление в системе.

Пример использования принципа:

Реакция 2SO₂ + O₂ 2SO₃ (г) экзотермична. Если повысить температуру, преимущество получит эндотермическая реакция разложения SО₃ и равновесие сместится влево. Если же понизить температуру, равновесие сместится вправо. Так, смесь SО₂ и О₂, взятых в стехиометрическом соотношении 2: 1 (, при температуре 400° С и атмосферном давлении превращается в SО₃ с выходом около 95%, т.е. состояние равновесия в этих условиях почти полностью смещено в сторону SО₃. При 600° С равновесная смесь содержит уже 76% SО₃, а при 800° С - только 25%. Именно поэтому при сжигании серы на воздухе образуется в основном SО₂ и лишь около 4% SО₃. Из уравнения реакции следует также, что повышение общего давления в системе будет сдвигать равновесие вправо, а при понижении давления равновесие будет смещаться влево.

Поверхностное и межфазное натяжение, работа адгезии и когезии, адсорбция, уравнение адсорбции Гиббса,они определяются.кой сталирхностное натяжение,краевой угол смачиванияений, характеристики смачивания и растекания.

Поверхностное натяжение или коэффициент поверхностного натяжения – величина, численно равная работе обратимого изотермического образования поверхности.

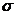
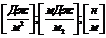
Поверхностное натяжение характеризует прочность межчастичных связей ( как и )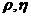

Чтобы увеличить или создать поверхность раздела фаз, нужно

затратить работу.

РАБОТА КОГЕЗИИ-это работа, затраченная против сил межчастичного взаимодействия при обратимом изотермическом разрыве столба однородной жидкости сечением, равным 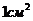, то есть это работа по созданию двух новых единиц поверхности.

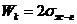
РАБОТА АДГЕЗИИ – работа, затрачиваемая по разрыву двух

несмешивающихся жидкостей на границе раздела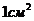

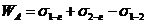1,2-жидкости.

АДСОРБЦИЯ_– это изменение поверхностного натяжения вещества под действием изменения состава поверхностного слоя.

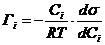- Адсорбция на поверхности раствора (формула Гиббса)

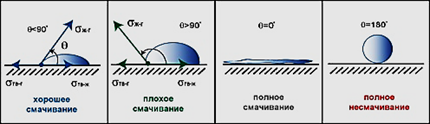
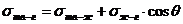
В состоянии равновесия:

Если 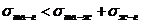-стягивание капли

Если 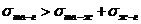- растекание капли.

Идеальный газ. Уравнение состояния. Закон Дальтона. Реальные газы.

Идеальный газ – газ, молекулы которого рассматриваются как невзаимодействующие друг с другом материальные точки.

Модель идеального газа:

1.Молекулы (атомы)принимаются за материальные точки с определенной массой.Размеры их ничтожны по сравнению с расстоянием между ними.

2.Молекулы(атомы) находятся в состоянии непрерывного и постоянного движения.

Между столкновениями они движутся прямолинейно. Движения равновероятны по всем направлениям.

3.Скорости частиц могут быть любыми.

4.При столкновении молекулы (атомы) ведут себя как упругие шары. Между частицами не действуют силы притяжения или отталкивания

Уравнение состояния(иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

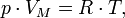
Где

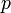— давление,

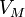— молярный объём,

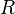— универсальная газовая постоянная

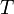— абсолютная температура,К.

Уравнения идеального газа

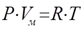
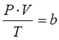
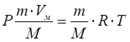
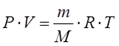
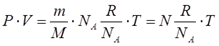
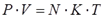
Реальные газы

При повышении плотности изменяются свойства газов – они перестают быть идеальными. Простейшим уравнением, которое качественно правильно описывает отличие реального газа от идеального, является уравнение Ван-дер-Ваальса

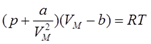
Закон Дальтона

Общее давление смеси идеальных газов равно сумме парциальных давлений компонентов.

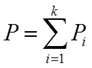
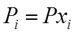, Xi-молярная доля i-го компонента в смеси.