Построение классической теории

В 1905 году Альбертом Эйнштейном была создана молекулярно-кинетическая теория для количественного описания броуновского движения.^[2]:13 В частности, он вывел формулу длякоэффициента диффузии сферических броуновских частиц^[3]:

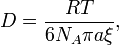
где 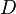— коэффициент диффузии, 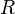— универсальная газовая постоянная, 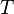— абсолютная температура, 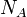— постоянная Авогадро, 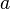— радиус частиц, 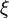— динамическая вязкость.

13)ЗаконМаксвеллаораспределениимолекулидеальногогазапоскоростямиэнергиямтепловогодвижения

При выводе основного уравнения молекулярно-кинетической теории молекулам зада­вали различные скорости. В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направ­лении в среднем движется одинаковое число молекул.

По молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул массой т₀ в газе, находящемся в состоянии равновесия при Т= const. остается постоянной и равной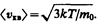

Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоро­стям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.

При выводе закона распределения молекул по скоростям Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Пред­полагалось также, что силовые поля на газ не действуют.

Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равныеdv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, т. е.

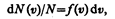
откуда

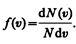
Применяя методы теории вероятностей. Максвелл нашел функцию f(v) — закон о распределеня молекул идеального газа по скоростям:

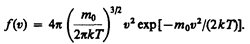(44.1)

Из (44.1) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т).

График функции (44.1) приведен на рис. 65. Так как при возрастании v множитель exp[–m₀v²/(2kT)] уменьшается быстрее, чем растет множитель v², то функция f(v), начинаясь от нуля, достигает максимума при v_B, и затем асимптотически стремится к нулю. Кривая несимметрична относительно v_B.

Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь заштрихованной полоски на рис. 65. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условию нормировки

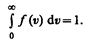
Скорость, при которой функция распределения молекул идеального газа по скоро­стям максимальна, называется наиболее вероятной скоростью. Значение наиболее веро­ятной скорости можнонайти продифференцировав выражение (44.1) (постоянные множители опускаем) по аргументу v, приравняв результат нулю и используя условие для максимума выражения f(v):

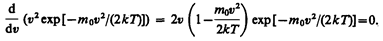
Значения v=0 и v=¥ соответствуют минимумам выражения (44.1), а значение v, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость v_B:

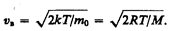(44.2)

Из формулы (44.2) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис. 66) сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, оста­ется неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.

14)Барометрическаяформула

Барометрическая формула Лапласа — зависимость давления или плотности газа от высоты в поле тяжести.

Для идеального газа, имеющего постоянную температуру и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения одинаково), барометрическая формула имеет следующий вид:

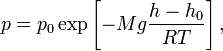
где 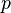— давление газа в слое, расположенном на высоте 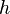, 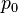— давление на нулевом уровне ( 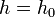), 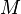— молярная масса газа, 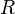— газовая постоянная, 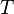— абсолютная температура. Из барометрической формулы следует, что концентрация молекул 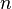(или плотность газа) убывает с высотой по тому же закону:

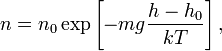
где 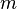— масса молекулы газа, 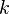— постоянная Больцмана.

Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Статистика Максвелла — Больцмана). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 году применил барометрическую формулу к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.

Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина 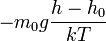, определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональной 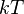. Чем выше температура 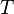, тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести 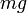(при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести 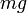может изменяться за счёт двух величин: ускорения 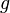и массы частиц .

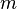Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.

Реальное распределение давления и плотности воздуха в земной атмосфере не следует барометрической формуле, так как в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.

Барометрическая формула лежит в основе барометрического нивелирования — метода определения разности высот 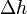между двумя точками по измеряемому в этих точках давлению ( 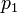и 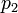). Поскольку атмосферное давление зависит от погоды, интервал времени между измерениями должен быть возможно меньшим, а пункты измерения располагаться не слишком далеко друг от друга. Барометрическая формула записывается в этом случае в виде: 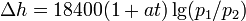(в м), где 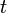— средняя температура слоя воздуха между точками измерения, 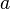— температурный коэффициент объёмного расширения воздуха. Погрешность при расчётах по этой формуле не превышает 0,1—0,5 % от измеряемой высоты. Более точна формула Лапласа, учитывающая влияние влажности воздуха и изменение ускорения свободного падения.

15)РаспределениеБольцмана

Распределение Больцмана — распределение вероятностей различных энергетических состоянийидеальной термодинамической системы (идеальный газ атомов или молекул) в условиях термодинамического равновесия; открыто Л. Больцманом в 1868—1871.

Согласно распределению Больцмана среднее число частиц с полной энергией 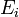равно

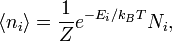
где 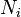— кратность состояния частицы с энергией 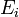— число возможных состояний частицы с энергией 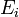. Постоянная 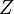находится из условия, что сумма 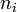по всем возможным значениям 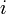равна заданному полному числу частиц 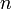в системе (условие нормировки):

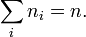
В случае, когда движение частиц подчиняется классической механике, энергию 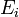можно считать состоящей из

§ кинетической энергии 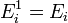(кин) частицы (молекулы или атома),

§ внутренней энергии 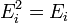(вн) (например, энергии возбуждения электронов) и

§ потенциальной энергии 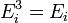(пот) во внешнем поле, зависящей от положения частицы в пространстве:

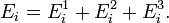
17)Опыт Штерна

Опыт Штерна — Герлаха — опыт немецких физиков Отто Штерна и Вальтера Герлаха, осуществлённый в 1922 году. Опыт подтвердил наличие уатомов спина (изначально в эксперименте участвовали атомы серебра, а потом и других металлов) и факт пространственного квантования направления их магнитных моментов.

Опыт состоял в следующем: пучок атомов серебра пропускали через сильно неоднородное магнитное поле, создаваемое мощным постоянныммагнитом. При прохождении атомов через это поле, в силу обладания ими магнитных моментов, на них действовала зависящая от проекции спина на направление магнитного поля сила, отклонявшая летящие между магнитами атомы от их первоначального направления движения. Причём, если предположить, что магнитные моменты атомов ориентированы хаотично (непрерывно), то тогда на расположенной далее по направлению движения атомов пластинке должна была проявиться размытая полоса. Однако вместо этого на пластинке образовались две достаточно чёткие узкие полосы, что свидетельствовало в пользу того, что магнитные моменты атомов вдоль выделенного направления принимали лишь два определённых значения, что подтверждало предположение квантово-механической теории о квантовании магнитного момента атомов.

Позднее с аналогичными результатами были проделаны опыты для пучков атомов других металлов, а также пучков протонов и электронов. Эти опыты доказали существование магнитного момента у рассмотренных частиц и показали их квантовую природу, явив собой доказательство постулатов квантовой теории.

18)Опыт Ламмерта

Опыт Ламмерта (1929) был проведён для подтверждения распределения Максвелла.

Суть эксперимента

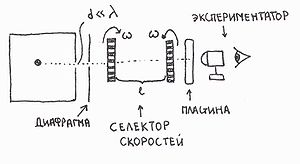
Опыт Ламмерта

На опыте (на рисунке) внутри ящика находится газ, молекулы которого вылетают через отверстие наружу. Диаметр отверстия много меньше длины свободного пробега молекул, молекул в ящике много, так что исчезновение вылетающих не меняет имеющееся распределение по скоростям внутри ящика. Колеса селектора, на поверхности которых находятся выступы, пропускающие или останавливающие летящие молекулы, вращаются с угловой скоростью 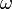. Так, преодолев первое колесо, молекула летит расстояние 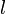до второго, которое за это время поворачивается на угол 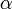. Выполняется соотношение

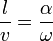
Так, регулируя 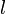, 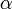и 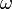, можно пропускать только молекулы с определенной скоростью 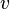. Пролетевшие через второе колесо молекулы оставляют след на пластине. Проведя эксперимент для различных значений 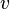, можно получить экспериментальную картину распределения скоростей в исследуемом газе. Так, с помощью этого эксперимента (в числе прочих) было подтверждено распределение Максвелла.

19)Явленияпереносавтермодинамическинеравновесныхсистемах

В термодинамически неравновесных системах возникают особые необратимые процес­сы, называемые явлениями переноса, в результате которых происходит пространствен­ный перенос энергии, массы, импульса. К явлениям переноса относятся теплопровод­ность (обусловлена переносом энергии),диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса). Для простоты ограничимся одномер­ными явлениями переноса. Систему отсчета выберем так, чтобы ось х была ориен­тирована в направлении переноса.

1. Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше,чем в другой, то с течением времени вследствие постоянных сто­лкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур.

Перенос энергии в форме теплоты подчиняетсязакону Фурье:

(48.1)

где j_E —плотность теплового потока — величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку,перпендикулярную оси х, l — теплопроводность, — градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры (поэтому знаки j_Eи – противоположны). Теплопроводность l численно равна плотности теплового потока при градиенте температуры, равном единице.

Можно показать, что

(48.2)

где с_V — удельная теплоемкость газа при постоянном объеме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объеме), r— плотность газа, <v> — средняя скорость теплового движения молекул, <l> — средняя длина сво­бодного пробега.

2. Диффузия. Явление диффузии заключается в том, что происходит самопроиз­вольное проникновение и перемешивание частиц двух соприкасающихся газов, жид­костей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Во время становления молекулярно-кинетической теории по вопросу диффузии возникли противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространяется довольно медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь с другими молекулами, в основном «стоят» на месте.

Явление диффузии для химически однородного газа подчиняется закону Фука:

(48.3)

где j_m —плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку,перпендикулярную оси х, D —диффузия (коэффициент диффузии), dr/dx — градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности (поэтому знаки j_m и dr/dx противоположны). Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице. Согласно кинети­ческой теории газов,

(48.4)

^ 3. Внутреннее трение (вязкость). Механизм возникновения внутреннего трения меж­ду параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

Согласно формуле (31.1), сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:

(48.5)

где h — динамическая вязкость (вязкость), dv/dx — градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению дви­жения слоев, S — площадь, на которую действует сила F.

Взаимодействие двух слоев согласно второму закону Ньютона можно рассматри­вать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе. Тогда выражение (48.5) можно пред­ставить в виде

(48.6)

где j_p —плотность потока импульса — величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении осих через единичную площадку, перпендикулярную оси х, — градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки j_р и противоположны).

Динамическая вязкость h численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле

(48.7)

Из сопоставления формул (48.1), (48.3) и (48.6), описывающих явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Эти законы были установлены задолго до того, как они были обоснованы и выведены из молекулярно-кинетической теории, позволившей установить, что внешнее сходство их математи­ческих выражений обусловлено общностью лежащего в основе явлений теплопровод­ности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения и столкновений друг с другом.

Рассмотренные законы Фурье, Фика и Ньютона не вскрывают молекулярно-кинетического смысла коэффициентов l, D и h. Выражения для коэффициентов переноса выводятся из кинетической теории. Они записаны без вывода, так как строгое рассмот­рение явлений переноса довольно громоздко, а качественное — не имеет смысла. Формулы (48.2), (48.4) и (48.7) связывают коэффициенты переноса и характеристики теплового движения молекул. Из этих формул вытекают простые зависимости между l, D и h:

Используя эти формулы, можно по найденным из опыта одним величинам определить другие.

20)Теплопроводность

Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.

Иногда теплопроводностью называется также количественная характеристика способности конкретного вещества проводить тепло. Численно эта характеристика равна количеству теплоты, проходящей через материал площадью 1 кв.м за единицу времени (секунду) при единичном температурном градиенте.

Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи. Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением объектов занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании их температуры.

Закон Фурье