Изопроцессы. Уравнения изопроцессов. Графики изопроцессов.

Изопроцессы. Уравнения изопроцессов. Графики изопроцессов.

Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма и адиабата соответственно.

Изобарный процесс — процесс изменения состояния термодинамической системы при постоянном давлении ( )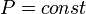

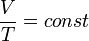
Зависимость объёма газа от температуры при неизменном давлении была экспериментально исследована в 1802 году Жозефом Луи Гей-Люссаком. Закон Гей-Люссака: При постоянном давлении и неизменных значениях массы газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.

Изохорный процесс

Основная статья: Изохорный процесс

Изохорный процесс — процесс изменения состояния термодинамической системы при постоянном объёме ( 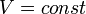). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:

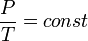
Линия, изображающая изохорный процесс на диаграмме, называется изохорой.

Ещё стоит указать что поданная к газу энергия расходуется на изменение внутренней энергии то есть Q = 3* ν*R*T/2=3*V*ΔP, где R — универсальная газовая постоянная, ν количество молей в газе, T температура в Кельвинах, V объём газа, ΔP приращение изменения давления. а линию, изображающая изохорный процесс на диаграмме, в осях Р(Т), стоит продлить и пунктиром соединить с началом координат, так как может возникнуть недопонимание.

Изотермический процесс — процесс изменения состояния термодинамической системы при постоянной температуре ( 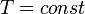)( )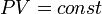. Изотермический процесс описывается законом Бойля — Мариотта:

При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остается постоянным: PV = const.

PV = constприT = const

Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии. Линия, изображающая адиабатный процесс на какой-либо термодинамической диаграмме, называется адиабатой.
Для идеальных газов адиабата имеет простейший вид и определяется уравнением:
pVk = const
где:
p — давление газа,
V — его объём,
k = Cp / Cv
Cp и Cv — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
Для нерелятивистского невырожденного одноатомного идеального газа k = 5/3, а для двухатомного газа k = 7/5.
Адиабатный процесс является частным случаем политропного процесса. Адиабатные процессы обратимы, если их проводить достаточно медленно (квазистатически). В общем случае адиабатный процесс необратим.

12) Молекулярно-кинетическая теория: основные положения, основное уравнение

Основное уравнение МКТ устанавливает связь между макроскопическим параметром «давление» и параметрами, характеризующими молекулу.

При своем движении молекулы ударяются о стенки сосуда, в котором находятся, создавая, таким образом, давление.

Определим некоторые условия: давление не зависит от формы сосуда, газ находится в равновесии. Рассмотрим газ в кубическом сосуде со стороной a. Будем считать, что все молекулы движутся в трех направлениях. Если число молекул N, то вдоль каждой координатной оси движется n*1/3 молекул.

При движении одной молекулы применим ЗСИ для системы «молекула-стенка».

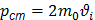
Сила давления, которая возникает, равна 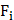. Тогда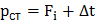

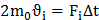- за время 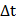молекула пробегает расстояние 2a.

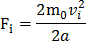
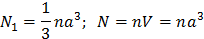
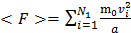В соответствии со статистическим методом, нужно применить среднее значение квадратичной скорости.

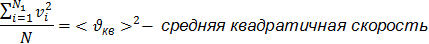
не имеет смысла в применении к одной молекуле

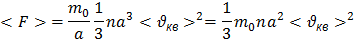
Давление – это сила, разделенная на единицу площади.

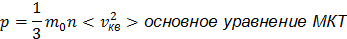
Следствия: , .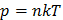

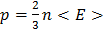Средняя кинетическая энергия поступательного движения молекул зависит прямо пропорционально от термодинамической температуры, поэтому температура является мерой средней кинетической энергии молекул. Температура характеризует состояние теплового равновесия, это величина аддитивная.

Температура - физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. В системе СИ разрешено использование термодинамической и практической шкалы температур. В термодинамической шкале тройная точка воды (температура, при которой лед, вода и пар при давлении 609 Па находятся в термодинамическом равновесии) считается равной Т = 273.16 градуса Кельвина [K]. В практической шкале температуры замерзания и кипения воды при давлении 101300 Па считаются равными, соответственно, t = 0 и t =100 градусов Цельсия [C]. Эти температуры связаны между собой соотношением

T = 273.15 + t.

Температура Т = 0 К называется нулем Кельвин, согласно современным представлениям эта температура недостижима, хотя приближение к ней сколь угодно близко возможно.

Из ОУМКТ можно получить формулу для расчета средней квадратичной скорости путем замены n=N/V, m=Nm₀.

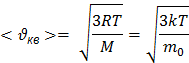
14 БИЛЕТ Магнитное поле. Его характеристики. Изображение магнитных полей. Принцип суперпозиции магнитных полей

Магнитное поле – форма материи. Свойство: действует на движущуюся заряженную частицу с силой, зависящей от произведения её заряда на скорость.

Магнитная индукция - силовая характеристика магнитного поля (вектор B). Определяется из закона Ампера: магнитная индукция B численно равна силе, действующей со стороны магнитного поля на единицу длины проводника, расположенного перпендикулярно к направлению магнитного поля, по которому течёт электрический ток единичной силы.

Поток вектора напряжённости электрического поля - сквозь замкнутую поверхность S: ò_(цирк,S)E_ndS. Это из теоремы Гаусса для вектора напряжённости E в диэлектрике = ò_(цирк,S)(e₀E_ndS)=S(q_СВОБ)+S(q_СВЯЗ). ГдеS(q_СВОБ) - это сумма свободных зарядов, охватываемых замкнутой поверхностью S, S(q_СВЯЗ) - это сумма связанных зарядов, охватываемых этой поверхностью.

Теорема Гаусса - магнитный поток сквозь произвольную замкнутую поверхность равен нулю: ò_{(цирку,S)}B_ndS=0. B_n - проекция вектора B на направление нормали . Теорема выражает отсутствие в природе магнитных зарядов и замкнутость линий индукции магнитного поля.

Маг-ное поле возникает около

Проводников с токов, т.к. электрический ток- направленное движение заряженных частиц, то магнитное поле создается

движущимися заряженными частицами. Магнитное поле зондируется с помощью

проводника с током, с помощью

магнитной стрелки. В каждую точку поля вносится замкнутый плоский контур с током.

Принцип супер позиции

Любой проводник с током может быть представлен совокупностью бесконечно малых векторов dl. Индукция результирующего магнитного поля, создаваемого всеми векторами dl, будет равна векторной сумме магнитных индукций, создаваемых каждым током dl в отдельности

15) Электрический ток. Характеристики электрического тока. Закон Ома.

Постоянный ток. Характеристики тока: сила тока, плотность. Закон Ома для однородного участка цепи в интегральном и дифференциальном видах. Сопротивление проводников. Проводимость проводников.

Ток - упорядоченное движение заряженных частиц.

Сила тока - сквозь некоторую поверхность S называется скалярная величина I, равная первой производной по времени от заряда q, проходящего через эту поверхность: I=dq/dt.

Постоянный ток - когда сила тока и его направление не изменяются с течением времени. Для постоянного тока: I=q/t, где q - электрический заряд, t - время. Сила постоянного тока численно равна заряду q, проходящему через поверхность S за единицу времени.

Распределение электрического тока по сечению S характеризуется вектором плотности тока j. Он направлен в сторону в сторону движения положительных зарядов и численно равен: j=dI/dS', где dS' - проекция элемента поверхности dS на плоскость, перпендикулярную к j, dI - сила тока сквозь dS и dS'.

Плотность тока (постоянного) - одинакова по всему сечению S проводника. Для постоянного тока I=jS.

Теория электропроводности по Друде - электрон имеет среднюю длину свободного пробега`l, равную по порядку величины периоду кристаллической решётки металла (10^-8см).

Закон Ома для произвольного участка цепи - IR₂₁=(j₁-j₂)+e₂₁ или U₂₁=IR₂₁. j1 и j2 - значение потенциала электрического поля в точках 1 и 2.

Закон Ома в дифференциальной форме - U21=ò_(1,2)((E_КУЛ+E_СТОР)dl)=ò_(1,2)(Edl). E=E_КУЛ+E_СТОР. E_КУЛ и E_СТОР - напряжённости кулоновских и сторонних сил.

19 БИЛЕТ Дифракция света. Дифракционная решетка, дифракция от решетки.

Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.

Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны и характерным размером неоднородностей среды , либо неоднородностей структуры самой волны. Наиболее заметно они проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, существенно превышающих длину волны (на 3—4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение

Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых.

Описание

Принцип Гюйгенса — Френеля является развитием принципа, который ввёл Христиан Гюйгенс в 1678 году: каждая точка поверхности, достигнутая световой волной, является вторичным источником световых волн. Огибающая вторичных волн становится фронтом волны в следующий момент времени. Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции. Огюстен Жан Френель в 1815 году дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса — Френеля и дифракционные явления.

Принцип Гюйгенса — Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.

Фронт световой волны разбивается штрихами решётки на отдельные пучки когерентного света. Эти пучки претерпевают дифракцию на штрихах и интерферируют друг с другом. Так как для разных длин волн максимумы интерференции оказываются под разными углами (определяемыми разностью хода интерферирующих лучей), то белый свет раскладывается в спектр.

29 БИЛЕТ Строение атома. Опыт Резерфорда. Постулаты Бора.

Изучая рассеяние альфа-частиц при прохождении через золотую фольгу, Резерфорд пришел к выводу, что весь положительный заряд атомов сосредоточен в их центре в очень массивном и компактном ядре. А отрицательно заряженные частицы (электроны) обращаются вокруг этого ядра. Эта модель коренным образом отличалась от широко распространенной в то время модели атома Томсона, в которой положительный заряд равномерно заполнял весь объем атома, а электроны были вкраплены в него. Несколько позже модель Резерфорда получила название планетарной модели атома (она действительно похожа на Солнечную систему: тяжелое ядро - Солнце, а обращающиеся вокруг него электроны - планеты).Постулаты бора.1.атомная система может находиться только в особых стационарных, или квантовых состояниях, каждому из которых соответствует определенная энергия Е(внизу кооф-т)n;в стационарном состоянии атом не излучает.m(e)*v(скор)*r(n)=nh.(n=1,2,3,...).2.при переходе атома из однородного стационарного состояния в другое испускается или поглощается квант электромагнитного излучения. Энергия фотона равна разности энергий атома в двух состояниях:

hV(ню)=Е(m)-E(n)

Постулаты Бора — основные допущения, сформулированные Нильсом Бором в 1913 году для объяснения закономерности линейчатого спектра атома водорода и водородоподобных ионов (формула Бальмера-Ридберга) и квантового характера испускания и поглощения света. Бор исходил из планетарной модели атома Резерфорда.

Атом может находиться только в особенных стационарных, или квантовых, состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн.

Электрон в атоме, не теряя энергии, двигается по определённым дискретным круговым орбитам, для которых момент импульса квантуется: , где — натуральные числа, а — постоянная Планка. Пребывание электрона на орбите определяет энергию этих стационарных состояний.

При переходе электрона с орбиты (энергетический уровень) на орбиту излучается или поглощается квант энергии , где — энергетические уровни, между которыми осуществляется переход. При переходе с верхнего уровня на нижний энергия излучается, при переходе с нижнего на верхний — поглощается.

Используя данные постулаты и законы классической механики, Бор предложил модель атома, ныне именуемую Боровской моделью атома[1]. В дальнейшем Зоммерфельд расширил теорию Бора на случай эллиптических орбит. Её называют моделью Бора-Зоммерфельда.

Атом водорода — физическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра может входить протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон преимущественно находится в тонком концентрическом шаровом слое вокруг атомного ядра, образуя электронную оболочку атома. Наиболее вероятный радиус электронной оболочки атома водорода в стабильном состоянии равен боровскому радиусу a0 = 0,529 Å.

Атом водорода имеет специальное значение в квантовой механике и релятивистской квантовой механике, поскольку для него проблема двух тел имеет точное или приближенное аналитическое решения. Эти решения применимы для разных изотопов водорода, с соответствующей коррекцией.

В квантовой механике атом водорода описывается двухчастичной матрицей плотности или двухчастичной волновой функцией. Также упрощенно рассматривается как электрон в электростатическом поле бесконечно тяжёлого атомного ядра, не участвующего в движении (или просто в кулоновском электростатическом потенциале вида 1/r). В этом случае атом водорода описывается редуцированной одночастичной матрицей плотности или волновой функцией.

В 1913 году Нильс Бор предложил модель атома водорода, имеющую множество предположений и упрощений, и вывел из неё спектр излучения водорода. Предположения модели не были полностью правильны, но тем не менее приводили к верным значениям энергетических уровней атома.

Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.

Из этого закона следует:

- Тела обладают свойствами инертности (свойство состоит в стремлении тел сохранить состояние покоя или равномерного прямолинейного движение).

- Система отсчета, в которой материальная точка, свободная от внешних воздействий либо покоится, либо движется равномерно и прямолинейно, называется инерциальной системой отсчета.

Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.

□ Если рассматривать действие различных сил на одно и то же тело, то оказывается, что ускорение прямо пропорционально равнодействующей приложенных сил: 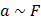и 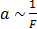. Можем записать, что 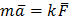. Это соотношение выражает второй закон Ньютона. ■

Ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). В СИ коэффициент k=1.

Векторная величина, равная произведению массы тела на его скорость и имеющая направление скорости, называется импульсом:

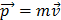
Выражение 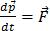- второй закон Ньютона в общем виде: скорость изменения импульса материальной точки равна действующей на неё силе.

Принцип независимости сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, как если бы других сил не было вообще.

Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют тела друг на друга, всегда равны по модулю и противоположно направлены, действуют вдоль прямой, соединяющей эти точки.

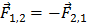
В любой системе тел, силы действуют попарно и являются силами одной природы.

Таким образом, 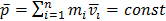– закон сохранения импульса: импульс замкнутой системы сохраняется, то есть не изменяется с течением времени. Закон сохранения импульса выполняется не только в классической физике. Закон носит универсальный характер и является фундаментальным законом природы.

В классической механике из-за независимости массы от скорости импульс системы может быть выражен через скорость её центра масс. Центром масс системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Её радиус-вектор равен:

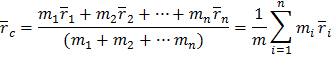
Если мы найдём производную от радиус-вектора, то мы найдём скорость, с которой движется центр масс. .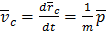

Центр масс системы движется так, как двигалась бы материальная точка с массой равной сумме масс системы тел под действием результирующей внешних сил. Для замкнутой системы сумма внешних сил равна 0, поэтому центр масс замкнутой системы движется равномерно и прямолинейно.

13) Работа в электрическом поле - Элементарная работа dA, совершаемая силой F, действующей на точечный электрический заряд q', находящийся в электрическом поле с напряжённостью E, равна dA=Fdlcos(F,dl)=q'Ecos(E,dl)dl, где dl - элементарное перемещение заряда, (E,dl) - угол между направлениями векторов E и dl. Полная работа A при конечном перемещении заряда q' из точки n в точку m поля равна: A=q'ò_(n,m)Edlcos(E,dl).

Потенциал поля - его энергетическая характеристика. Потенциал в данной точке поля - это скалярная величина, численно равная потенциальной энергии W_П единичного положительного заряда, помещённого в эту точку: j=W_П/q.

Разность потенциалов - Работа, которая совершается силами электростатического поля при перемещении точечного электрического заряда q, равна произведению этого заряда на разность потенциалов в начальной 1 и конечной 2 точках пути: A=W_П1-W_П2=q(j₁-j₂)

Потенциал поля точечного заряда - j=q/4pe₀er, где r - расстояние точки поля, обладающей потенциалом j, от заряда q, e - относительная диэлектрическая проницаемость среды, e₀ - электрическая постоянная

принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции позволяет рассчитать электростатические поля любой си­стемы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

14) Магнитное поле – форма материи. Свойство: действует на движущуюся заряженную частицу с силой, зависящей от произведения её заряда на скорость.

Магнитная индукция - силовая характеристика магнитного поля (вектор B). Определяется из закона Ампера: магнитная индукция B численно равна силе, действующей со стороны магнитного поля на единицу длины проводника, расположенного перпендикулярно к направлению магнитного поля, по которому течёт электрический ток единичной силы.

Поток вектора напряжённости электрического поля - сквозь замкнутую поверхность S: ò_(цирк,S)E_ndS. Это из теоремы Гаусса для вектора напряжённости E в диэлектрике = ò_(цирк,S)(e₀E_ndS)=S(q_СВОБ)+S(q_СВЯЗ). Где S(q_СВОБ) - это сумма свободных зарядов, охватываемых замкнутой поверхностью S, S(q_СВЯЗ) - это сумма связанных зарядов, охватываемых этой поверхностью.

Принцип суперпозиции магнитных полей: если магнитное поле создано несколькими проводниками с токами, то вектор магнитной индукции в какой-либо точке этого поля равен векторной сумме магнитных индукций, созданных в этой точке каждым током в отдельности:

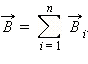Изопроцессы. Уравнения изопроцессов. Графики изопроцессов.

Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма и адиабата соответственно.

Изобарный процесс — процесс изменения состояния термодинамической системы при постоянном давлении ( )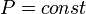

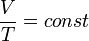
Зависимость объёма газа от температуры при неизменном давлении была экспериментально исследована в 1802 году Жозефом Луи Гей-Люссаком. Закон Гей-Люссака: При постоянном давлении и неизменных значениях массы газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.

Изохорный процесс

Основная статья: Изохорный процесс

Изохорный процесс — процесс изменения состояния термодинамической системы при постоянном объёме ( 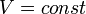). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:

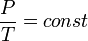
Линия, изображающая изохорный процесс на диаграмме, называется изохорой.

Ещё стоит указать что поданная к газу энергия расходуется на изменение внутренней энергии то есть Q = 3* ν*R*T/2=3*V*ΔP, где R — универсальная газовая постоянная, ν количество молей в газе, T температура в Кельвинах, V объём газа, ΔP приращение изменения давления. а линию, изображающая изохорный процесс на диаграмме, в осях Р(Т), стоит продлить и пунктиром соединить с началом координат, так как может возникнуть недопонимание.

Изотермический процесс — процесс изменения состояния термодинамической системы при постоянной температуре ( 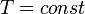)( )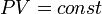. Изотермический процесс описывается законом Бойля — Мариотта:

При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остается постоянным: PV = const.

PV = constприT = const

Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии. Линия, изображающая адиабатный процесс на какой-либо термодинамической диаграмме, называется адиабатой.
Для идеальных газов адиабата имеет простейший вид и определяется уравнением:
pVk = const
где:
p — давление газа,
V — его объём,
k = Cp / Cv
Cp и Cv — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
Для нерелятивистского невырожденного одноатомного идеального газа k = 5/3, а для двухатомного газа k = 7/5.
Адиабатный процесс является частным случаем политропного процесса. Адиабатные процессы обратимы, если их проводить достаточно медленно (квазистатически). В общем случае адиабатный процесс необратим.

12) Молекулярно-кинетическая теория: основные положения, основное уравнение

Основное уравнение МКТ устанавливает связь между макроскопическим параметром «давление» и параметрами, характеризующими молекулу.

При своем движении молекулы ударяются о стенки сосуда, в котором находятся, создавая, таким образом, давление.

Определим некоторые условия: давление не зависит от формы сосуда, газ находится в равновесии. Рассмотрим газ в кубическом сосуде со стороной a. Будем считать, что все молекулы движутся в трех направлениях. Если число молекул N, то вдоль каждой координатной оси движется n*1/3 молекул.

При движении одной молекулы применим ЗСИ для системы «молекула-стенка».

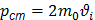
Сила давления, которая возникает, равна 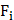. Тогда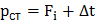

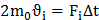- за время 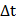молекула пробегает расстояние 2a.

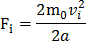
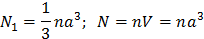
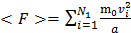В соответствии со статистическим методом, нужно применить среднее значение квадратичной скорости.

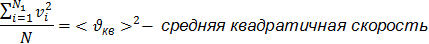
не имеет смысла в применении к одной молекуле

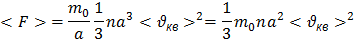
Давление – это сила, разделенная на единицу площади.

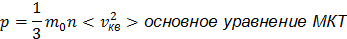
Следствия: , .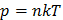

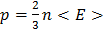Средняя кинетическая энергия поступательного движения молекул зависит прямо пропорционально от термодинамической температуры, поэтому температура является мерой средней кинетической энергии молекул. Температура характеризует состояние теплового равновесия, это величина аддитивная.

Температура - физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. В системе СИ разрешено использование термодинамической и практической шкалы температур. В термодинамической шкале тройная точка воды (температура, при которой лед, вода и пар при давлении 609 Па находятся в термодинамическом равновесии) считается равной Т = 273.16 градуса Кельвина [K]. В практической шкале температуры замерзания и кипения воды при давлении 101300 Па считаются равными, соответственно, t = 0 и t =100 градусов Цельсия [C]. Эти температуры связаны между собой соотношением

T = 273.15 + t.

Температура Т = 0 К называется нулем Кельвин, согласно современным представлениям эта температура недостижима, хотя приближение к ней сколь угодно близко возможно.

Из ОУМКТ можно получить формулу для расчета средней квадратичной скорости путем замены n=N/V, m=Nm₀.

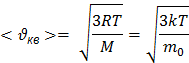
14 БИЛЕТ Магнитное поле. Его характеристики. Изображение магнитных полей. Принцип суперпозиции магнитных полей

Магнитное поле – форма материи. Свойство: действует на движущуюся заряженную частицу с силой, зависящей от произведения её заряда на скорость.

Магнитная индукция - силовая характеристика магнитного поля (вектор B). Определяется из закона Ампера: магнитная индукция B численно равна силе, действующей со стороны магнитного поля на единицу длины проводника, расположенного перпендикулярно к направлению магнитного поля, по которому течёт электрический ток единичной силы.

Поток вектора напряжённости электрического поля - сквозь замкнутую поверхность S: ò_(цирк,S)E_ndS. Это из теоремы Гаусса для вектора напряжённости E в диэлектрике = ò_(цирк,S)(e₀E_ndS)=S(q_СВОБ)+S(q_СВЯЗ). ГдеS(q_СВОБ) - это сумма свободных зарядов, охватываемых замкнутой поверхностью S, S(q_СВЯЗ) - это сумма связанных зарядов, охватываемых этой поверхностью.

Теорема Гаусса - магнитный поток сквозь произвольную замкнутую поверхность равен нулю: ò_{(цирку,S)}B_ndS=0. B_n - проекция вектора B на направление нормали . Теорема выражает отсутствие в природе магнитных зарядов и замкнутость линий индукции магнитного поля.

Маг-ное поле возникает около

Проводников с токов, т.к. электрический ток- направленное движение заряженных частиц, то магнитное поле создается

движущимися заряженными частицами. Магнитное поле зондируется с помощью

проводника с током, с помощью

магнитной стрелки. В каждую точку поля вносится замкнутый плоский контур с током.

Принцип супер позиции

Любой проводник с током может быть представлен совокупностью бесконечно малых векторов dl. Индукция результирующего магнитного поля, создаваемого всеми векторами dl, будет равна векторной сумме магнитных индукций, создаваемых каждым током dl в отдельности

15) Электрический ток. Характеристики электрического тока. Закон Ома.

Постоянный ток. Характеристики тока: сила тока, плотность. Закон Ома для однородного участка цепи в интегральном и дифференциальном видах. Сопротивление проводников. Проводимость проводников.

Ток - упорядоченное движение заряженных частиц.

Сила тока - сквозь некоторую поверхность S называется скалярная величина I, равная первой производной по времени от заряда q, проходящего через эту поверхность: I=dq/dt.

Постоянный ток - когда сила тока и его направление не изменяются с течением времени. Для постоянного тока: I=q/t, где q - электрический заряд, t - время. Сила постоянного тока численно равна заряду q, проходящему через поверхность S за единицу времени.

Распределение электрического тока по сечению S характеризуется вектором плотности тока j. Он направлен в сторону в сторону движения положительных зарядов и численно равен: j=dI/dS', где dS' - проекция элемента поверхности dS на плоскость, перпендикулярную к j, dI - сила тока сквозь dS и dS'.

Плотность тока (постоянного) - одинакова по всему сечению S проводника. Для постоянного тока I=jS.

Теория электропроводности по Друде - электрон имеет среднюю длину свободного пробега`l, равную по порядку величины периоду кристаллической решётки металла (10^-8см).

Закон Ома для произвольного участка цепи - IR₂₁=(j₁-j₂)+e₂₁ или U₂₁=IR₂₁. j1 и j2 - значение потенциала электрического поля в точках 1 и 2.

Закон Ома в дифференциальной форме - U21=ò_(1,2)((E_КУЛ+E_СТОР)dl)=ò_(1,2)(Edl). E=E_КУЛ+E_СТОР. E_КУЛ и E_СТОР - напряжённости кулоновских и сторонних сил.

19 БИЛЕТ Дифракция света. Дифракционная решетка, дифракция от решетки.

Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.

Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны и характерным размером неоднородностей среды , либо неоднородностей структуры самой волны. Наиболее заметно они проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, существенно превышающих длину волны (на 3—4 порядка и более), явлением дифракции, к