Уравнение Максвелла для электромагнитного поля.

Уравнения Максвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее, влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму (одним из ярчайших примеров здесь может служить специальная теория относительности).

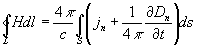-первое уравнение.

то есть циркуляция вектора напряжённости магнитного поля вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый отрезок dl контура) определяется полным током через произвольную поверхность S, ограниченную данным контуром. Здесь j_n — проекция плотности тока проводимости j на нормаль к бесконечно.

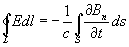- второе уравнение.

то есть циркуляция вектора напряжённости электрического поля вдоль замкнутого контура L (эдс индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S, ограниченную данным контуром. Здесь B_n — проекция на нормаль к площадке ds вектора магнитной индукции В; знак минус соответствует Ленца правилу (См. Ленца правило) для направления индукционного тока.

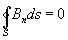- третье уравнение.

то есть поток вектора магнитной индукции через произвольную замкнутую поверхность S равен нулю.

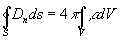- четвёртое уравнение.

то есть поток вектора электрической индукции через произвольную замкнутую поверхность S определяется электрическим зарядом, находящимся внутри этой поверхности (в объёме V, ограниченном данной поверхностью).

Гармонические колебания и их основные характеристики. Гармонический осциллятор. Маятники. Сложение гармонических колебаний. Свободные затухающие механические колебания. Вынужденные механические колебания. Резонанс.

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебания широко распространены в окружающем мире и могут иметь самую различную природу. Это могут быть механические (маятник), электромагнитные (колебательный контур) и другие виды колебаний.
Свободными, или собственными колебаниями, называются колебания, которые происходят в системе предоставленной самой себе, после того как она была выведена внешним воздействием из состояния равновесия. Примером могут служить колебания шарика, подвешенного на нити.
Особую роль в колебательных процессах имеет простейший вид колебаний - гармонические колебания. Гармонические колебания лежат в основе единого подхода при изучении колебаний различной природы, так как колебания, встречающиеся в природе и технике, часто близки к гармоническим, а периодические процессы иной формы можно представить как наложение гармонических колебаний.

Гармоническими колебанияминазываются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса иликосинуса.
Уравнение гармонических колебаний имеет вид:

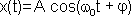, где A - амплитуда колебаний(величина наибольшего отклонения системы от положения равновесия); 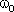-круговая частота.

Период гармонических колебаний равен: T = 2π/ .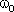
Число колебаний в единицу времени называется частотой колебаний ν.
Частота гармонических колебаний равна: ν = 1/T. Единица измерения частоты герц (Гц) - одно колебание в секунду.
Круговая частота 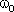= 2π/T = 2πν дает число колебаний за 2π секунд.

Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы 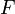, пропорциональной смещению 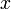(согласно закону Гука):

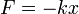
где k — положительная константа, описывающая жёсткость системы.

Если 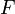— единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Маятник — система, подвешенная в поле тяжести и совершающая механические колебания. Колебания совершаются под действием силы тяжести, силы упругости и силы трения. Во многих случаях трением можно пренебречь, а от сил упругости (либо сил тяжести) абстрагироваться, заменив их связями.

Во время колебаний маятника происходят постоянные превращения энергии из одного вида в другой. Кинетическая энергия маятника превращается в потенциальную энергию (гравитационную, упругую) и обратно. Кроме того, постепенно происходит диссипация кинетической энергии в тепловую за счёт сил трения.

Одним из простейших маятников является шарик, подвешенный на нити. Идеализацией этого случая является математический маятник — механическая система, состоящая из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести.

Маятник Фуко — это груз, подвешенный на нити, способный изменять плоскость своих колебаний.

Ещё одним простейшим маятником является пружинный маятник. Пружинный маятник — это груз, подвешенный на пружине и способный колебаться вдоль вертикальной оси.

Крутильный маятник — механическая система, представляющая собой тело, подвешенное в поле тяжести на тонкой нити и обладающее лишь одной степенью свободы: вращением вокруг оси, задаваемой неподвижной нитью.

Сложение гармонических колебаний - колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача - найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний - нахождение траектории результирующего колебания.

Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний постепенно уменьшается (затухает).Во многих случаях в первом приближении можно считать, что при небольших скоростях силы, вызывающие затухание колебаний, пропорциональны величине скорости (например маятник). Тогда сила трения (или сопротивления)

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ - колебания, происходящие под действием внешней переменной силы (вынуждающей силы).

Установившиеся вынужденные колебания происходят с частотой, равной частоте вынуждающей силы.

Рассмотрим вынужденные колебания на примере реального (с трением) пружинного маятника. Будем отталкиваться от уравнения движения (второй закон Ньютона), которое мы написали для затухающих колебаний. При наличии дополнительной вынуждающей силы F(t) необходимо дописать ее в правую часть уравнения. В каноническом виде дифференциальное уравнение вынужденных механических колебаний имеет вид:

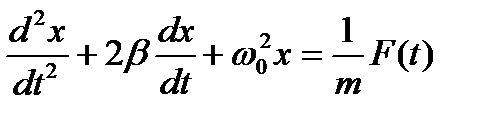
Для пружинного маятника:

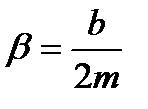
Резонанс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.

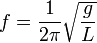- Резонансную частоту