Применение силы Лоренца-В электроприборах

Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы

Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например, в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД генераторах.

В ускорителях заряженных частиц-Сила Лоренца также используется в ускорителях заряженных частиц, задавая орбиту, по которой движутся эти частицы.

44. Явление электромагнитной индукции (опыты Фарадея). ЭДС индукции. Правило Ленца.

явление электромагнитной индукции заключается в появлении (наведении) в проводящем контуре, находящемся в магнитном поле, электродвижущей силы в случае изменения величины магнитного потока, проходящего через поверхность, ограниченную этим контуром.При этом имеется в виду весь магнитный поток окружающий контур, т.е. создаваемый как внешними магнитными полями, так и током, протекающим в самом контуре. Кроме того, несущественно чем вызвано изменение магнитного потока. Он может изменяться в результате перемещения контура или поля друг относительно друга, или в результате изменения токов в цепях, создающих магнитный поток.

Как известно, электрические токи порождают вокруг себя магнитное поле. Связь магнитного поля с током дала толчок к многочисленным попыткам возбудить ток в контуре с помощью магнитного поля. Эта фундаментальное открытие было блестяще сделано в 1831 г. английским физиком М. Фарадеем, который открыл явленение электромагнитной индукции. Оно говорит о том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.

Приведем классические опыты Фарадея, с помощью которых было открыто явление электромагнитной индукции.

Опыт I (рис. 1а). Если в соленоид, который замкнут на гальванометр, вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания мы видим отклонение стрелки гальванометра (возникает индукционный ток); при этом отклонения стрелки при вдвигании и выдвигании магнита имеют противоположные направления. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При смене в опытеполюсов магнита направление отклонения стрелки также изменится. Для получения индукционного тока можно оставлять магнит неподвижным, тогда нужно относительно магнита перемещать соленоид.

Опыт II. Концы одной из катушек, которая вставлена одна в другую, присоединяются к гальванометру, а через другую катушку пропускается ток. В моменты включения или выключения тока наблюдается отклонение стрелки гальванометра, а также в моменты его уменьшения или увеличения, а также при перемещении катушек друг относительно друга (рис. 1б). Направления отклонений стрелки гальванометра также имею противоположные направления при включении или выключении тока, его увеличении или уменьшении, приближении или удалении катушек.Исследуя результаты своих многочисленных опытов, Фарадей пришел к заключению, что индукционный ток возникает всегда, когда в опыте осуществляется изменение сцепленного с контуром потока магнитной индукции. Например, при повороте в однородном магнитном поле замкнутого проводящего контура в нем также появляется индукционный ток - в этом случае индукция магнитного поля вблизи контура остается постоянной, а меняется только поток магнитной индукции сквозь контур. В результате опыта было также установлено, что значение индукционного тока абсолютно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения (также в опытах Фарадея доказывается, что отклонение стрелки гальванометра (сила тока) тем больше, чем больше скорость движения магнита, или скорость изменения силы тока, или скорость движения катушек).

Открытие явления электромагнитной индукции имело огромное значение, поскольку была дана возможность получения электрического тока с помощью магнитного поля. Этим оьткрытие дало взаимосвязь между электрическими и магнитными явлениями, что в дальнейшем послужило толчком для разработки теории электромагнитного поля.

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением 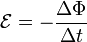где Φ — поток магнитного поля через замкнутую поверхность S, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре.

Правило Ленца, правило для определения направления индукционного тока: Индукционный ток, возникающий при относительном движении проводящего контура и источника магнитного поля, всегда имеет такое направление, что его собственный магнитный поток компенсирует изменения внешнего магнитного потока, вызвавшего этот ток.

Если ток увеличивается, то и магнитный поток увеличивается.Если 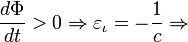индукционныйток направлен против основного тока.Если 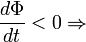индукционный ток направлен в том же направлении, что и основной ток.Индукционный ток всегда направлен так, чтобы уменьшить действие причины его вызывающей.В обобщенной формулировке правило Ленца гласит, что индукционный ток всегда направлен так, чтобы противодействовать вызвавшей его первопричине.

45.Самоиндукция и индуктивность. Проявление индуктивности в электрических цепях.

Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контурепри изменении тока, протекающего по контуру.При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Этим свойством ЭДС самоиндукции сходна с силой инерции. Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока I: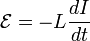

Эл.ток создает собственное магнитное поле . Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике

(B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I).

ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника

(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.

Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.Индуктивность - физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.Также индуктивность можно рассчитать по формуле: 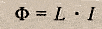где Ф - магнитный поток через контур, I - сила тока в контуре.

Единицы измерения индуктивности в системе СИ:Гн.Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды.

Катушка индуктивности в электрической цепи хорошо проводит постоянный ток и в то же время оказывает сопротивление переменному току, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.

46. Энергия и плотность энергии магнитного поля.

Энергия магнитного поля -энергия, связанная с магнитным полем и преобразующаяся в другие формы энергии при изменении магнитного поля.Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида.Плотность энергии магнитного поля - физическая величина, равная отношению:

- энергии магнитного поля в некотором объеме; к

- величине этого объема.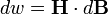,где: H-напряжённость магнитного поля, В- магнитная индукция.

47. Взаимодействие магнитного поля с веществом. Магнитное поле в веществе.

При взаимодействии вещества с магнитным полем одной из характеристик, определяющей это взаимодействие, является магнитная восприимчивость χ, которая показывает способность вещества приобретать определенную намагниченность М под действием внешнего магнитного поля. Намагниченность связана с напряженностью зависимостью 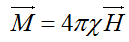Магнитная восприимчивость зависит от многих факторов: напряженности магнитного поля Н, температуры давления, способа изготовления, термообработки и химического состав, а также от «магнитной предыстории» материала.

В зависимости от модуля и знака магнитной восприимчивости χ все вещества условно делят на диамагнетики, парамагнетики и ферромагнетики.Диамагнетики имеют отрицательную магнитную восприимчивость: χ = –(10-5 … 10-7), т. е. они намагничиваются во внешнем магнитном поле навстречу вектору напряженности этого поля. Примерами диамагнетиков являются Si, Bi, Au, Cu и другие вещества, а также некоторые органические и неорганические вещества.Парамагнетикинамагничиваются во внешнем магнитном поле по направлению вектора его напряженности, т. е. имеют положительную магнитную восприимчивость: χ = (10-1 … 10-5). К ним относятся Al, Pt, Cr, Mn, ферромагнетики при температурах, превышающих температуру Кюри.Ферромагнетики – магнитные материалы, в которых наблюдается явление самопроизвольного образования магнитных доменов со взаимно параллельными спинами .

До сих пор рассматривалось магнитное поле, которое создавалось проводниками с током или движущимися электрическими зарядами, находящимися в вакууме. Если же магнитное поле создается не в вакууме, а в какой-то другой среде, то магнитное поле изменяется. Это объясняется тем, что различные вещества, помещенные в магнитное поле, намагничиваются и сами становятся источниками магнитного поля. Вещества, способные намагничиваться в магнитном поле, называются магнетиками. Намагниченное вещество создает магнитное поле с индукцией , которое накладывается на магнитное поле с индукцией , обусловленное токами. Оба поля в сумме дают результирующее поле, магнитная индукция которого равна

. Для объяснения намагничивания тел Ампер предположил, что в молекулах вещества циркулируют круговые токи. Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствие внешнего магнитного поля молекулярные токи ориентированы хаотически, поэтому суммарный магнитный момент вещества равен нулю. В магнитном поле молекулярные токи ведут себя подобно рамке с током, то есть ориентируются так, чтобы магнитные моменты были преимущественно ориентированы вдоль магнитного поля, вследствие чего магнетик намагничивается. Природа молекулярных токов стала понятной только в начале ХХ в., когда Резерфордом было установлено, что атомы всех веществ состоят из положительно заряженного ядра и движущихся вокруг него отрицательно заряженных электронов. В 1913 г. Нильс Бор развил теорию, согласно которой электроны в атомах движутся по круговым орбитам. Это движение можно рассматривать как круговой ток, обладающий магнитным моментом, называемым орбитальным магнитным моментом электрона. Позднее было показано, что теория Бора имеет ограниченную применимость и во многих отношениях совершенно неверна. Тем не менее, согласно современным представлениям, электроны в атомах обладают орбитальным магнитным моментом. Кроме того, электрон имеет собственный магнитный момент, называемый спиновым магнитным моментом. Магнитный момент многоэлектронного атома будет векторной суммой орбитальных и спиновых моментов всех его электронов.

Именно взаимодействием магнитных моментов атомов с внешним магнитным полем и обусловлено намагничивание веществ и, следовательно, изменение магнитного поля в веществе. Для описания этого поля вводят величину m, которая называется относительной магнитной проницаемостью или просто магнитной проницаемостью вещества. Магнитная проницаемость показывает, во сколько раз значение магнитной индукции в веществе отличается от ее значения в вакууме при тех же значениях токов, создающих магнитное поле. Магнитная проницаемость зависит от рода вещества и от его состояния, например, от температуры.

48. Электрический колебательный контур. Собственные колебания. Формула Томсона.

Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока.Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания

Резонансная частота контура определяется так называемой формулой Томсона: 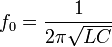Колебательный контур состоит из двух основных частей: катушки индуктивности и конденсатора. Катушка представляет собой некоторое число витков медной проволоки, а простейший конденсатор – две металлические пластинки, разделённые слоем диэлектрика. Чем больше площадь пластин и чем ближе они расположены одна к другой, тем при прочих равных условиях большей электрической ёмкостью обладает конденсатор. На величину ёмкости влияет и то, из какого вещества состоит диэлектрик. Конденсатор заряжают от какого-то источника тока, затем подключают катушку индуктивности. Конденсатор разряжается, но в силу индуктивности катушки ток в контуре нарастает постепенно, а потом начнет заряжать конденсатор (в противоположном направлении), и так будет колебаться довольно долго, смотря что за конденсатор поставили. Колебания в контуре, происходящие без какого-либо влияния со стороны, чрезвычайно кратковременны. Это объясняется тем, что электрический ток нагревает провода катушки. При этом энергия электрических колебаний превращается в тепло, которое рассеивается. Потери эти неизбежны, поэтому колебания в контуре быстро затухают. Для того чтобы получить незатухающие колебания, нужно особое устройство, которое подает к колебательному контуру всё новые и новые порции энергии.

Собственные колебания, свободные колебания, колебания в механической, электрической или какой-либо другой физической системе, совершающиеся при отсутствии внешнего воздействия за счёт первоначально накопленной энергии (вследствие наличия начального смещения или начальной скорости). Характер С. к. определяется главным образом собственными параметрами системы (массой, индуктивностью, ёмкостью, упругостью). В реальных системах вследствие рассеяния энергии С. к. всегда затухающие, а при больших потерях они становятся апериодическими.Простейшими примерами свободных колебания являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

Формула Томсона - формула, выражающая зависимость периода незатухающих собственных колебаний, возникающих в колебательном контуре, от индуктивности и емкости этого контура.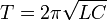

49.Затухающие колебания. Уравнение, график и характеристики.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида 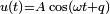Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний или её квадрата.

Получим дифференциальное уравнение свободных затухающих колебаний на примере реального пружинного маятника, совершающего колебания в среде с сопротивлением (простейший случай - трение о воздух). Пусть масса маятника m, коэффициент упругости пружины k, сила сопротивления, действующая на маятник, F = - bv, v - скорость маятника, b - коэффициент сопротивления среды, в которой находится маятник. Так как мы рассматриваем только линейные системы, b = const, k = const. x - смещение маятника от положения равновесия. Второй закон Ньютона в нашем случае запишется так: 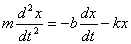Это уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. 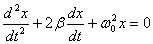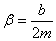Его, однако, принято записывать в следующем, так называемом каноническом виде: ,где - коэффициент затухания, 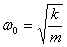- собственная частота свободных (незатухающих) колебаний пружинного маятника, то, что раньше мы обозначали просто w.

Уравнение затухающих колебаний в таком (каноническом) виде описывает затухающие колебания всех линейных систем; конкретная колебательная система отличается только выражениями для b и j0.

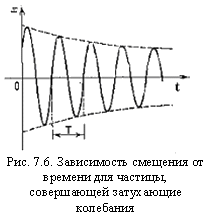
Экспериментальный график затухающих колебаний при малом коэффициенте затухания представлен на рис. 7.6. Из рис. 7.6 видно, что график зависимости x=x(t).выглядит как косинус, умноженный на некоторую функцию, которая убывает со временем. Эта функция представлена на рисунке штриховыми линиями. Простой функцией, которая ведет себя подобным образом, является экспоненциальная функция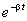

Чем меньше силы трения в системе, тем медленнее затухают колебания, тем лучше колебательная система. Для характеристики качества колебательной системы вводится ряд параметров:

t = 1/b - время релаксации затухающих колебаний (за t амплитуда уменьшается в e раз). 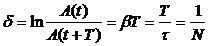- логарифмический декремент затухания; N - число колебаний, в течение которых амплитуда уменьшается в e раз. Соответственно, exp(bT) - просто декремент затухания. 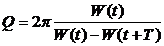- добротность колебательной системы; W(t) - энергия (полная) колебательной системы в момент времени t.

50. Вынужденные колебания. Резонанс.

Вынужденные колебания, колебания, возникающие в какой-либо системе под действием переменной внешней силы (например, колебания мембраны телефона под действием переменного магнитного поля, колебания механической конструкции под действием переменной нагрузки и т.д.). Характер В. к. определяется как характером внешней силы, так и свойствами самой системы. В начале действия периодической внешней силы характер В. к. изменяется со временем (в частности, В. к. не являются периодическими), и лишь по прошествии некоторого времени в системе устанавливаются периодические В. к. с периодом, равным периоду внешней силы (установившиеся В. к.). Установление В. к. в колебательной системе происходит тем быстрее, чем больше затухание колебаний в этой системе.

Резона́нс(фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.

51.Переменный ток. Мгновенное, среднее и действующее значения переменного тока. Закон Ома для цепи переменного тока.

Переме́нный ток,— электрический ток, который периодически изменяется по модулю и направлению.

Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону.В устройствах-потребителях постоянного тока переменный ток часто преобразуется выпрямителями для получения постоянного тока.Важной характеристикой П. т. является его частота f — число периодов в 1 сек: f = 1/Т