Основные положения молекулярно-кинетической теории
Основные положения молекулярно-кинетической теории
Великому американскому физику Ричарду Фейнману, автору знаменитого курса «Фейнмановские лекции по физике», принадлежат замечательные слова:
Если бы в результате какой-то мировой катастрофы все накопленные научные знания оказались бы уничтоженными и к грядущим поколениям живых существ перешла бы только одна фраза, то какое утверждение, составленное из наименьшего количества слов, принесло бы наибольшую информацию? Я считаю, что это — атомная гипотеза (можете называть ее не гипотезой, а фактом, но это ничего не меняет): все тела состоят из атомов — маленьких телец, которые находятся в беспрерывном движении, притягиваются на небольшом расстоянии, но отталкиваются, если одно из них плотнее прижать к другому. В одной этой фразе...содержится невероятное количество информации о мире, стоит лишь приложить к ней немного воображения и чуть соображения.
В этих словах заключена суть молекулярно-кинетической теории (МКТ) строения вещества. А именно, основными положениями МКТ являются следующие три утверждения.
1. Любое вещество состоит из мельчайших частиц — молекул и атомов. Они расположены в пространстве дискретно, то есть на некоторых расстояниях друг от друга.
2. Атомы или молекулы вещества находятся в состоянии беспорядочного движения[1], которое никогда не прекращается.
3. Атомы или молекулы вещества взаимодействуют друг с другом силами притяжения и отталкивания, которые зависят от расстояний между частицами.
Эти положения являются обобщением многочисленных наблюдений и экпериментальных фактов. Давайте рассмотрим подробнее эти положения и приведём их опытное обоснование.
Атомы и молекулы
Возьмём бумажный листок и начнём делить его на всё более и более мелкие части. На каждом ли шаге мы будем получать кусочки именно бумаги, или на каком-то этапе появится нечто новое?
Первое положение МКТ говорит нам о том, что вещество не является делимым до бесконечности. Рано или поздно мы дойдём до «последнего рубежа» — мельчайших частиц данного вещества. Эти частицы — атомы и молекулы. Их также можно разделить на части, но тогда исходное вещество прекратит своё существование.
Атом — это наименьшая частица данного химического элемента, сохраняющая все его химические свойства. Химических элементов не так много — все они сведены в таблицу Менделеева.
Молекула — это наименьшая частица данного вещества (не являющегося химическим элементом), сохраняющая все его химические свойства. Молекула состоит из двух или более атомов одного или нескольких химических элементов.
Например, H2O — это молекула воды, состоящая из двух атомов водорода и одного атома кислорода. Разделив её на атомы, мы перестанем иметь дело в веществом под названием «вода». Далее, разделив атомы H и O на составные части, мы получим набор протонов, нейтронов и электронов и тем самым потеряем информацию о том, что поначалу это были водород и кислород.
Размер атома или молекулы (состоящей из небольшого числа атомов) составляет порядка 10−8 см. Это настолько малая величина, что атом невозможно разглядеть ни в какой оптический микроскоп.
Атомы и молекулы называются для краткости просто частицами вещества. Чем именно является частица — атомом или молекулой — в каждом конкретном случае установить нетрудно. Если речь идёт о химическом элементе, то частицей будет атом; если же рассматривается сложное вещество, то его частица — это молекула, состоящая из нескольких атомов.
Далее, первое положение МКТ утверждает, что частицы вещества не заполняют пространство непрерывно. Частицы расположены дискретно, то есть как бы в отдельных точках. Между частицами имеются промежутки, величина которых может меняться в некоторых пределах.
В пользу первого положения МКТ свидетельствует явление теплового расширения тел. А именно, при нагревании увеличиваются расстояния между частицами вещества, и размеры тела возрастают. При охлаждении, наоборот, расстояния между частицами уменьшаются, в результате чего тело сжимается.
Ярким подтверждением первого положения МКТ служит также диффузия — взаимное проникновение соприкасающихся веществ друг в друга.
Например, на рис. 1 показан[2]процесс диффузии в жидкости. Частицы растворимого вещества помещены в стакан с водой и расположены вначале в верхней левой части стакана. С течением времени частицы перемещаются (как говорят, диффундируют) из области высокой концентрации в область низкой концентрации. В конце концов концентрация частиц становится везде одинаковой — частицы равномерно распределяются по всему объёму жидкости.
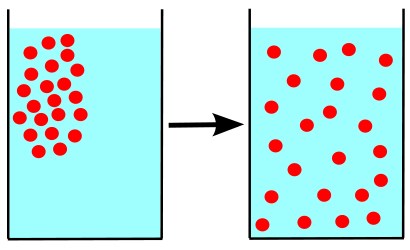
Рис. 1. Диффузия в жидкости
Как объяснить диффузию с точки зрения молекулярно-кинетической теории? Очень просто: частицы одного вещества проникают в промежутки между частицами другого вещества. Диффузия идёт тем быстрее, чем больше эти промежутки — поэтому легче всего смешиваются друг с другом газы (в которых расстояния между частицами много больше размеров самих частиц).
Газы
Газы — самый простой объект для изучения в молекулярно-кинетической теории. Почему? Дело в том, что средние расстояния между частицами газов намного превышают размеры самих частиц. В промежутках между соударениями частицы газа проходят расстояния, на несколько порядков превышающие собственные размеры (рис. 3).
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAx5hUYsUA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWsCMRSE7wX/Q3iFXopmt5aqW6MsQkHpodR68Pjc PJPFzcuySXX990Yo9DjMzDfMfNm7RpypC7VnBfkoA0FceV2zUbD7+RhOQYSIrLHxTAquFGC5GDzM sdD+wt903kYjEoRDgQpsjG0hZagsOQwj3xIn7+g7hzHJzkjd4SXBXSNfsuxNOqw5LVhsaWWpOm1/ nQJsv3bW48bsX6efp3iYlc+5KZV6euzLdxCR+vgf/muvtYJJPob7mXQE5OIGAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQDHmFRixQAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA " adj="0,,0" path="m1270000,1651000l1270000,,,,,1651000r1270000,xe" filled="f" strokecolor="#b2b2b2" strokeweight="1pt">
Рис. 3. Частицы газа
Например, в воздухе при нормальных условиях длина свободного пробега молекулы составляет примерно 10−5 см. Это на три порядка превышает средний размер молекулы (10−8 см).
При таких больших расстояниях между частицами силы межмолекулярного взаимодействия оказываются весьма незначительными. Во многих ситуациях взаимодействием частиц газа на расстоянии можно пренебречь и учитывать лишь их соударения друг с другом. Вот почему изучать газы гораздо проще, чем жидкости или твёрдые тела.
Не испытывая сильного притяжения со стороны других частиц, любая частица газа обладает полной свободой передвижения и может оказаться в любом месте сосуда. Поэтому газы не имеют ни фиксированной формы, ни фиксированного объёма. Мы можем поместить данную порцию газа в какой угодно сосуд, и газ неизменно займёт весь предоставленный ему объём. В зависимости от объёма сосуда будут изменяться лишь средние расстояния между частицами газа.
Способность газов менять свой объём находит широчайшее применение в технике. Функционирование тепловых двигателей и многих других устройств основано в конечном счёте на том, что газ при расширении перемещает поршень и совершает работу.
Твёрдые тела
Если сравнивать с газами, то твёрдые тела являются их полной противоположностью. Ни о какой свободе передвижения частицы твёрдых тел даже «не помышляют».
В твёрдых телах частицы расположены весьма близко друг к другу: расстояния между частицами порядка размера самих частиц. Силы взаимодействия между частицами твёрдого тела очень велики; расположение частиц в пространстве обладает периодической повторяемостью и образует так называемую кристаллическую решётку.
Например, на рис. 4 представлена пространственная модель кристаллической решётки кремния[4]. Шарики — это атомы кремния, а трубки между шариками изображают силы взаимодействия между атомами.
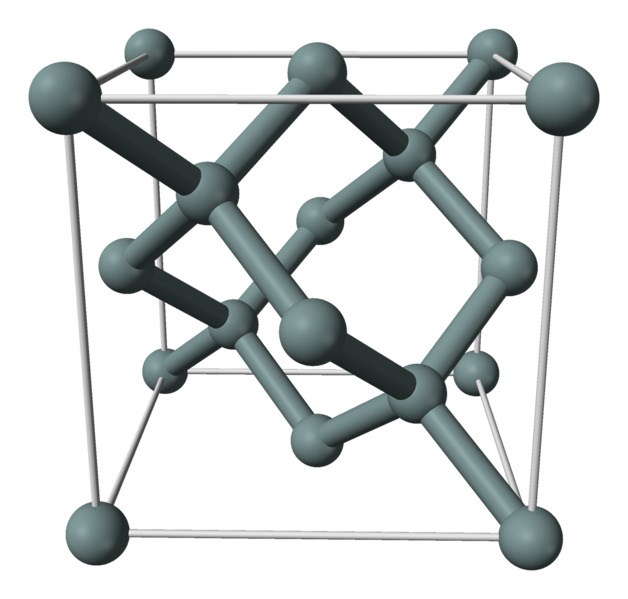
Рис. 4. Пространственная модель кристаллической решётки
Атомы кремния, как видите, расположены в пространстве периодическим образом, причём каждый атом сцеплен с четырьмя другими атомами. На рис. 5 мы видим плоское изображение той же самой кристаллической решётки (вдобавок показаны электроны, находящиеся на внешних оболочках атомов кремния).
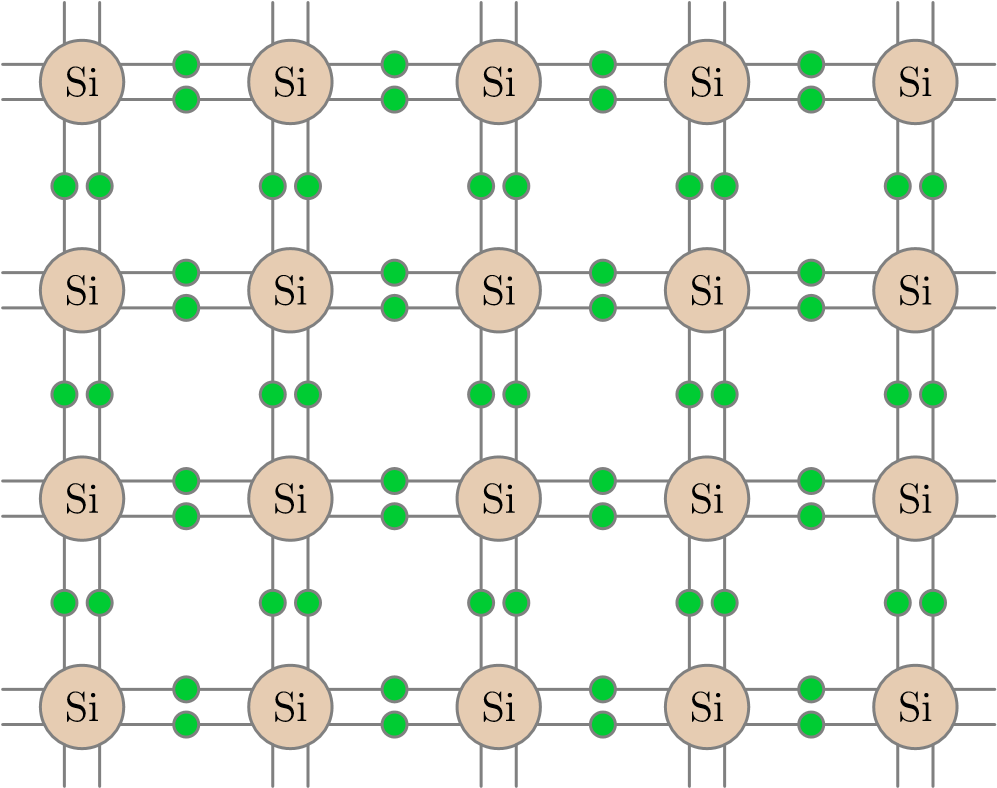
Рис. 5. Плоское изображение кристаллической решётки
Точки пространства, в которых находятся частицы твёрдого тела, называются узлами кристаллической решётки.
На самом деле частицы не покоятся в узлах кристаллической решётки, а совершают тепловое движение — колеблются относительно этих самых узлов. Таким образом, узел кристаллической решётки — это положение равновесия частицы, в небольшой окрестности которого частица постоянно находится. Чтобы покинуть область своего обитания (выскочить из узла), частице нужна очень большая энергия; произойти такое событие может лишь при чрезвычайно редком стечении обстоятельств. Имея столь жёсткую внутреннюю структуру, твёрдое тело сохраняет неизменными свою форму и свой объём.
Жидкости
По своим свойствам жидкости занимают промежуточное положение между газами и твёрдыми телами: жидкости сохраняют объём, но не форму. Мы можем говорить об одном литре воды, переливая её из сосуда в сосуд; но при этом вода принимает форму сосуда.
Как и в твёрдых телах, частицы жидкости упакованы весьма плотно и совершают колебания около некоторых положений равновесия. Попытка сжатия жидкости немедленно приводит к деформациям самих молекул и встречает мощное сопротивление: жидкости, в отличие от газов, практически не сжимаемы.
Однако, в отличие от твёрдых тел, частица жидкости не привязана навсегда к своему положению равновесия: спустя некоторое время она скачком меняет его на новое положение и колеблется в окружении новых частиц. Затем — новый скачок, новый период «осёдлой жизни», и так далее (рис. 6). Если частицы твёрдых тел можно сравнить с людьми, имеющими свой дом, то частицы жидкостей — это кочевники, постоянно меняющие места своих стоянок.
Рис. 6. «Осёдло-кочевая жизнь» молекулы жидкости
На рисунке мы видим молекулу жидкости, время от времени меняющую место своего расположения. «Ореол», окружающий молекулу, изображает область осёдлой жизни, внутри которой молекула совершает тепловые колебания. Теоретические расчёты показывают, что за время осёдлой жизни молекула совершает несколько десятков-сотен колебаний внутри области осёдлой жизни.
Силы притяжения между частицами жидкости достаточно велики для того, чтобы объём сохранялся фиксированным. Но ограниченность времени осёдлой жизни частиц придаёт жидкостям текучесть: жидкости не сохраняют форму.
Рассмотрим для примера воду в стакане. Скачки молекул из одного осёдлого положения в другое происходят равновероятно по всем направлениям. Но если стакан наклонить, то в определённых участках воды сила тяжести задаст преимущественное направление этих скачков, и форма воды в стакане поменяется. Таково в общих чертах объяснение текучести.
Температура
Мы часто используем слово «температура» в повседневной речи. А что такое температура? В данном разделе мы объясним физический смысл этого понятия.
В молекулярной физике и термодинамике рассматриваются макроскопические тела, т.е. тела, состоящие из огромного числа частиц. Например, в стакане воды содержится порядка 102[5]молекул. Такое грандиозное число с трудом поддаётся осмыслению.
Термодинамическая система
Термодинамической системой называется макроскопическое тело или система тел, которые могут взаимодействовать друг с другом и с окружающими телами. Стакан с водой — пример термодинамической системы.
Термодинамическая система состоит из столь большого числа частиц, что совершенно невозможно описывать её поведение путём рассмотрения движения каждой молекулы в отдельности. Однако именно грандиозность числа молекул делает ненужным такое описание.
Оказывается, что состояние термодинамической системы можно характеризовать небольшим числом макроскопических параметров — величин, относящимся к системе в целом, а не к отдельным атомам или молекулам. Такими макроскопическими параметрами являются давление, объём, температура, плотность, теплоёмкость, удельное сопротивление и др.
Состояние термодинамической системы, при котором все макроскопические параметры остаются неизменными с течением времени, называется тепловым равновесием. В состоянии теплового равновесия прекращаются все макроскопические процессы: диффузия, теплопередача, фазовые переходы, химические реакции и т.д.5
Термодинамическая система называется изолированной, если она не может обмениваться энергией с окружающими телами. Чай в термосе — типичный пример изолированной системы.
Тепловое равновесие
Фундаментальный постулат, вытекающий из многочисленных опытных данных, гласит: каково бы ни было начальное состояние тел изолированной системы, со временем в ней устанавливается тепловое равновесие. Таким образом, тепловое равновесие — это состояние, в которое любая система, изолированная от окружающей среды, самопроизвольно переходит через достаточно большой промежуток времени.
Температура как раз и является величиной, характеризующей состояние теплового равновесия термодинамической системы.
Температура — это макроскопический параметр, значения которого одинаковы для всех частей термодинамической системы, находящейся в состоянии теплового равновесия. Попросту говоря, температура — это то, что является одинаковым для любых двух тел, которые находятся в тепловом равновесии друг с другом. При тепловом контакте тел с одинаковыми температурами между ними не будет происходить обмен энергией (теплообмен).
В общем же случае при установлении между телами теплового контакта теплообмен начнётся. Говорят, что тело, которое отдаёт энергию, имеет более высокую температуру, а тело, которое получает энергию — более низкую температуру. Температура, таким образом, указывает направление теплообмена между телами. В процессе теплообмена температура первого тела начнёт уменьшаться, температура второго тела — увеличиваться; при выравнивании температур теплообмен прекратится — наступит тепловое равновесие.
Особенность температуры заключается в том, что она не аддитивна: температура тела не равна сумме температур его частей. Этим температура отличается от таких физических величин, как масса, длина или объём. И по этой причине температуру нельзя измерить путём сравнения с эталоном.
Измеряют температуру с помощью термометра.
Для создания термометра выбирают какое-либо вещество (термометрическое вещество), какую-либо характеристику этого вещества (термометрическую величину), и используют зависимость термометрической величины от температуры. При этом выбор термометрического вещества и термометрической величины может быть весьма произвольным.
Так, в бытовых жидкостных термометрах термометрическим веществом является ртуть (или спирт), а термометрической величиной — длина столбика жидкости. Здесь используется линейная зависимость объёма жидкости от температуры.
В идеально-газовых термометрах используется линейная зависимость давления разреженного газа (близкого по своим свойствам к идеальному) от температуры.
Действие электрических термометров (термометров сопротивления) основано на температурной зависимости сопротивления чистых металлов, сплавов и полупроводников.
В процессе измерения температуры термометр приводится в тепловой контакт[6]с телом, температура которого определяется. Показания термометра после наступления теплового равновесия — это и есть температура тела. При этом термометр показывает свою температуру!
Изопроцессы
На протяжении этого раздела мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:
• m = const, то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;
• µ = const, то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).
Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.
Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).
Термодинамический процесс
Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.
Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
1. Изотермический процесс идёт при постоянной температуре газа: T = const.
2. Изобарный процесс идёт при постоянном давлении газа: p = const.
3. Изохорный процесс идёт при постоянном объёме газа: V = const.
Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.
Изотермический процесс
При изотермическом процессе температура газа постоянна. В ходе процесса меняются только давление газа и его объём.
Установим связь между давлением p и объёмом V газа в изотермическом процессе. Пусть температура газа равна T. Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны p1,V1,T, а во втором — p2,V2,T. Эти значения связаны уравнением Менделеева — Клапейрона:
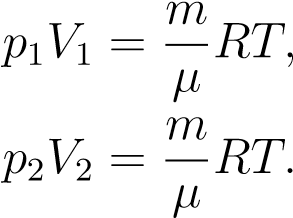
Как мы сказали с самого начала, масса газа m и его молярная масса µ предполагаются неизменными. Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части: p1V1 = p2V2.
Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:
pV = const.
Данное утверждение называется законом Бойля — Мариотта. Записав закон Бойля — Мариотта в виде
const
p = ,
V
можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.
Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.
Изобарный процесс
Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.
Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня M и поперечное сечение поршня S, то давление газа всё время постоянно и равно
,
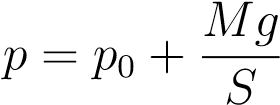где p0 — атмосферное давление.
Пусть идеальный газ совершает изобарный процесс при давлении p. Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны p,V1,T1 и p,V2,T2.
Выпишем уравнения состояния:
,
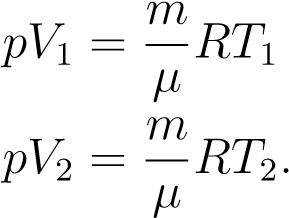Поделив их друг на друга, получим:
.
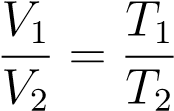В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):
.
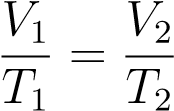А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:
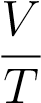= const.
Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре: V = const · T.
Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.
Графики изобарного процесса
График изобарного процесса называется изобарой. На V T-диаграмме изобара V = const · T является прямой линией (рис. 10):
| T |
| V |
| изобара |
Рис. 10. Изобара на V T-диаграмме
Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.
Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на V T-диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями p1 и p2 (рис. 11):
| T |
| V |
| p |
| > |
| p |
| p |
| T |
| V |
| V |
Рис. 11. Чем ниже изобара, тем больше давление
Зафиксируем некоторое значение температуры T. Мы видим, что V2 < V1. Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).
Стало быть, p2 > p1.
В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси p (рис. 12):
p p
| V |
| T |
Рис. 12. Изобары на pV - и pT-диаграммах
Изохорный процесс
Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.
Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).
Пусть идеальный газ совершает изохорный процесс в сосуде объёмом V . Опять-таки рассмотрим два произвольных состояния газа с параметрами p1,V,T1 и p2,V,T2. Имеем:
,
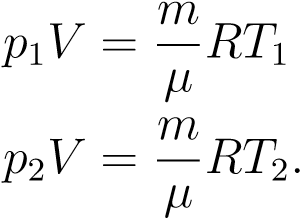Делим эти уравнения друг на друга:
.
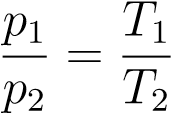Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:
.
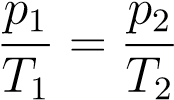Ввиду произвольности выбора состояний мы приходим к закону Шарля:
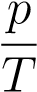= const.
Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре: p = const · T.
Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.
Графики изохорного процесса
График изохорного процесса называется изохорой. На pT-диаграмме изохора p = const · T является прямой линией (рис. 13):
| T |
| p |
| изохора |
Рис. 13. Изохора на pT-диаграмме
Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.
Далее, чем больше объём, тем ниже идёт изохора на pT-диаграмме (рис. 14):
| T |
| p |
| V |
| > |
| V |
| V |
| T |
| p |
| p |
Рис. 14. Чем ниже изохора, тем больше объём
Доказательство аналогично предыдущему. Фиксируем температуру T и видим, что p2 < p1. Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, V2 > V1.
В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси V (рис. 15):
| изохора | |
| T |
| V |
| изохора |
V
Рис. 15. Изохоры на pV - и V T-диаграммах
Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами. Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
Насыщенный пар
Если открытый стакан с водой оставить на долгое время, то в конце концов вода полностью улетучится. Точнее — испарится. Что такое испарение и почему оно происходит?
Испарение и конденсация
При данной температуре молекулы жидкости обладают разными скоростями. Скорости большинства молекул находятся вблизи некоторого среднего значения (характерного для этой температуры). Но попадаются молекулы, скорости которых значительно отличаются от средней как в меньшую, так и б´ольшую сторону.
На рис. 16 изображён примерный график распределения молекул жидкости по скоростям. Голубым фоном показано то самое большинство молекул, скорости которых группируются около среднего значения. Красный «хвост» графика — это небольшое число «быстрых» молекул, скорости которых существенно превышают среднюю скорость основной массы молекул жидкости.
| Скоростьмолекул |
| Числомолекул |
| Быстрыемолекулы |
Рис. 16. Распределение молекул по скоростям
Когда такая весьма быстрая молекула окажется на свободной поверхности жидкости (т.е. на границе раздела жидкости и воздуха), кинетической энергии этой молекулы может хватить на то, чтобы преодолеть силы притяжения остальных молекул и вылететь из жидкости. Данный процесс и есть испарение, а молекулы, покинувшие жидкость, образуют пар.
Итак, испарение — это процесс превращения жидкости в пар, происходящий на свободной поверхности жидкости[7].
Может случиться, что через некоторое время молекула пара вернётся обратно в жидкость. Процесс перехода молекул пара в жидкость называется конденсацией. Конденсация пара — процесс, обратный испарению жидкости.
Динамическое равновесие
А что будет, если сосуд с жидкостью герметично закрыть? Плотность пара над поверхностью жидкости начнёт увеличиваться; частицы пара будут всё сильнее мешать другим молекулам жидкости вылетать наружу, и скорость испарения станет уменьшаться. Одновременно начнёт увеличиваться скорость конденсации, так как с возрастанием концентрации пара число молекул, возвращающихся в жидкость, будет становиться всё больше.
Наконец, в какой-то момент скорость конденсации окажется равна скорости испарения. Наступит динамическое равновесие между жидкостью и паром: за единицу времени из жидкости будет вылетать столько же молекул, сколько возвращается в неё из пара. Начиная с этого момента количество жидкости перестанет убывать, а количество пара — увеличиваться; пар достигнет «насыщения».
Насыщенный пар — это пар, который находится в состоянии динамического равновесия со своей жидкостью. Пар, не достигший состояния динамического равновесия с жидкостью, называется ненасыщенным.
Давление и плотность насыщенного пара обозначаются pн и ρн. Очевидно, pн и ρн — это максимальные давление и плотность, которые может иметь пар при данной температуре. Иными словами, давление и плотность насыщенного пара всегда превышают давление и плотность ненасыщенного пара.
Свойства насыщенного пара
Оказывается, что состояние насыщенного пара (а ненасыщенного — тем более) можно приближённо описывать уравнением состояния идеального газа (уравнением Менделеева — Клапейрона). В частности, имеем приближённое соотношение между давлением насыщенного пара и его плотностью:
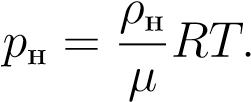(6)
Это весьма удивительный факт, подтверждаемый экспериментом. Ведь по своим свойствам насыщенный пар существенно отличается от идеального газа. Перечислим важнейшие из этих отличий.
1. При неизменной температуре плотность насыщенного пара не зависит от его объёма.
Если, например, насыщенный пар изотермически сжимать, то его плотность в первый момент возрастёт, скорость конденсации превысит скорость испарения, и часть пара конденсируется в жидкость — до тех пор, пока вновь не наступит динамическое равновесие, в котором плотность пара вернётся к своему прежнему значению.
Аналогично, при изотермическом расширении насыщенного пара его плотность в первый момент уменьшится (пар станет ненасыщенным), скорость испарения превысит скорость конденсации, и жидкость будет дополнительно испаряться до тех пор, пока опять не установится динамическое равновесие — т.е. пока пар снова не станет насыщенным с прежним значением плотности.
2. Давление насыщенного пара не зависит от его объёма.
Это следует из того, что плотность насыщенного пара не зависит от объёма, а давление однозначно связано с плотностью уравнением (6).
Как видим, закон Бойля — Мариотта, справедливый для идеальных газов, для насыщенного пара не выполняется. Это и не удивительно — ведь он получен из уравнения Менделеева — Клапейрона в предположении, что масса газа остаётся постоянной.
3. При неизменном объёме плотность насыщенного пара растёт с повышением температуры и уменьшается с понижением температуры.
Действительно, при увеличении температуры возрастает скорость испарения жидкости. Динамическое равновесие в первый момент нарушается, и происходит дополнительное испарение некоторой части жидкости. Пара будет прибавляться до тех пор, пока динамическое равновесие вновь не восстановится.
Точно так же при понижении температуры скорость испарения жидкости становится меньше, и часть пара конденсируется до тех пор, пока не восстановится динамическое равновесие — но уже с меньшим количеством пара.
Таким образом, при изохорном нагревании или охлаждении насыщенного пара его масса меняется, поэтому закон Шарля в данном случае не работает. Зависимость давления насыщенного пара от температуры уже не будет линейной функцией.
4. Давление насыщенного пара растёт с температурой быстрее, чем по линейному закону.
В самом деле, с увеличением температуры возрастает плотность насыщенного пара, а согласно уравнению (6) давление пропорционально произведению плотности на температуру.
Зависимость давления насыщенного пара от температуры является экспоненциальной (рис. 17). Она представлена участком 1–2 графика. Эту зависимость нельзя вывести из законов идеального газа.
| T |
| p |
Рис. 17. Зависимость давления пара от температуры
В точке 2 вся жидкость испаряется; при дальнейшем повышении температуры пар становится ненасыщенным, и его давление растёт линейно по закону Шарля (участок 2–3).
Вспомним, что линейный рост давления идеального газа вызван увеличением интенсивности ударов молекул о стенки сосуда. В случае нагревания насыщенного пара молекулы начинают бить не только сильнее, но и чаще — ведь пара становится больше. Одновременным действием этих двух факторов и вызван экспоненциальный рост давления насыщенного пара.
Влажность воздуха
Воздух, содержащий водяной пар, называется влажным. Чем больше пара находится в воздухе, тем выше влажность воздуха.
Абсолютная влажность — это парциальное давление водяного пара, находящегося в воздухе (т.е. давление, которое водяной пар оказывал бы сам по себе, в отсутствие других газов). Иногда абсолютной влажностью называют также плотность водяного пара в воздухе.
Относительная влажность воздуха ϕ — это отношение парциального давления водяного пара в нём к давлению насыщенного водяного пара при той же температуре. Как правило, это
отношение выражают в процентах:
p ϕ = · 100%.
pн
Из уравнения Менделеева-Клапейрона (6) следует, что отношение давлений пара равно отношению плотностей. Так как само уравнение (6), напомним, описывает насыщенный пар лишь приближённо, мы имеем приближённое соотношение:
ρ ϕ = · 100%. ρн
Одним из приборов, измеряющих влажность воздуха, является психрометр. Он включает в себя два термометра, резервуар одного из которых завёрнут в мокрую ткань. Чем ниже влажность, тем интенсивнее идёт испарение воды из ткани, тем сильнее охлаждается резервуар «мокрого» термометра, и тем больше разность его показаний и показаний сухого термометра. По этой разности с помощью специальной психрометрической таблицы определяют влажность воздуха.
Внутренняя энергия
Частицы любого тела — атомы или молекулы — совершают хаотическое непрекращающееся движение (так называемое тепловое движение). Поэтому каждая частица обладает некоторой кинетической энергией.
Кроме того, частицы вещества взаимодействуют друг с другом силами электрического притяжения и отталкивания, а также посредством ядерных сил. Стало быть, вся система частиц данного тела обладает ещё и потенциальной энергией.
Кинетическая энергия теплового движения частиц и потенциальная энергия их взаимодействия вме<