Криволинейные и поверхностные интегралы.

Криволинейные и поверхностные интегралы часто встречаются в физике. Они бывают двух видов, первый из которых рассматривается здесь. Этот
тип интегралов строится согласно общей схеме, по которой вводятся определённые, двойные и тройные интегралы. Коротко напомним эту схему.
Имеется некоторый объект, по которому проводится интегрирование (одномерный, двумерный или трёхмерный). Этот объект разбивается на малые части,
в каждой из частей выбирается точка. В каждой из этих точек вычисляется значение подынтегральной функции и умножается на меру той части, которой
принадлежит данная точка (длину отрезка, площадь или объём частичной области). Затем все такие произведения суммируются, и выполняется предельный
переход к разбиению объекта на бесконечно малые части. Получающийся предел и называется интегралом.

1. Определение криволинейного интеграла первого рода

Рассмотрим функцию 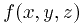, определённую на кривой 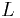. Кривая предполагается спрямляемой. Напомним, что это означает, грубо говоря,
что в кривую можно вписать ломаную со сколь угодно малыми звеньями, причём в пределе бесконечно большого числа звеньев длина ломаной должна оставаться
конечной. Кривая разбивается на частичные дуги длиной 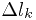и на каждой из дуг выбирается точка 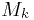. Составляется произведение ,
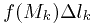проводится суммирование по всем частичным дугам 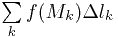. Затем осуществляется предельный переход с устремлением длины наибольшей
из частичных дуг к нулю. Предел является криволинейным интегралом первого рода
.
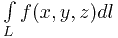Важной особенностью этого интеграла, прямо следующей из его определения, является независимость от направления интегрирования, т.е.
.

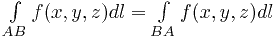2. Определение поверхностного интеграла первого рода

Рассмотрим функцию 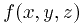, определённую на гладкой или кусочно-гладкой поверхности 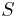. Поверхность разбивается на частичные области
с площадями 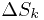, в каждой такой области выбирается точка 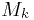. Составляется произведение 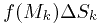, проводится суммирование
по всем частичным областям 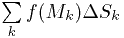. Затем осуществляется предельный переход с устремлением диаметра наибольшей из всех частичных
областей к нулю. Предел является поверхностным интегралом первого рода
.

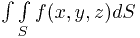3. Вычисление криволинейного интеграла первого рода

Методика вычисления криволинейного интеграла первого рода просматривается уже из формальной его записи, а фактически следует непосредственно из
определения. Интеграл сводится к определённому, только нужно записать дифференциал дуги 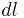кривой, вдоль которой проводится интегрирование.
Начнём с простого случая интегрирования вдоль плоской кривой, заданной явным уравнением 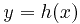. В этом случае дифференциал дуги
.
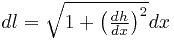Затем в подынтегральной функции выполняется замена переменной 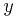, и интеграл принимает вид
,
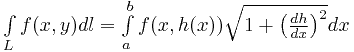где отрезок 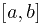отвечает изменению переменной 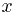вдоль той части кривой, по которой проводится интегрирование.

Очень часто кривая задаётся параметрически, т.е. уравнениями вида 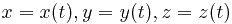. Тогда дифференциал дуги
.
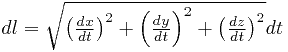Формула эта очень просто обосновывается. По сути, это теорема Пифагора. Дифференциал дуги - фактически длина бесконечно малой части кривой.
Если кривая гладкая, то её бесконечно малую часть можно считать прямолинейной. Для прямой имеет место соотношение
.
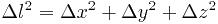Чтобы оно выполнялось для малой дуги кривой, следует от конечных приращений перейти к дифференциалам:
.
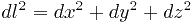Если кривая задана параметрически, то дифференциалы просто вычисляются:
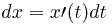и т.д.
Соответственно, после замены переменных в подынтегральной функции криволинейный интеграл вычисляется следующим образом:
,
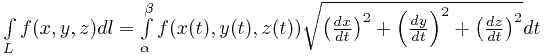где части кривой, по которой проводится интегрирование соответствует отрезок изменения параметра .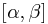

Несколько сложнее обстоит дело в случае, когда кривая задаётся в криволинейных координатах. Этот вопрос обычно обсуждается в рамках дифференциальной
геометрии. Приведём формулу для вычисления интеграла вдоль кривой, заданной в полярных координатах уравнением :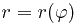
.
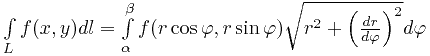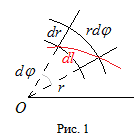
Приведём обоснование и для дифференциала дуги в полярных координатах. Подробное обсуждение построения координатной сетки полярной системы координат
см. здесь. Выделим малую дугу кривой, расположенную по отношению к координатным линиям так, как показано на рис. 1. В силу малости всех фигурирующих
дуг снова можно применить теорему Пифагора и записать:
.
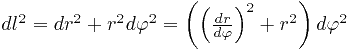Отсюда и следует искомое выражение для дифференциала дуги.

С чисто теоретической точки зрения достаточно просто понять, что криволинейный интеграл первого рода должен сводиться к своему частному случаю -
определённому интегралу. Действительно, выполняя замену, которая диктуется параметризацией кривой, вдоль которой вычисляется интеграл, мы устанавливаем
взаимно-однозначное отображение между частью данной кривой и отрезком изменения параметра 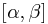. А это и есть сведение к интегралу
вдоль прямой, совпадающей с координатной осью - определённому интегралу.

4. Вычисление поверхностного интеграла первого рода

После предыдущего пункта должно быть ясно, что одна из основных частей вычисления поверхностного интеграла первого рода - запись элемента поверхности ,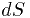
по которой выполняется интегрирование. Опять-таки начнём с простого случая поверхности, заданной явным уравнением 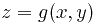. Тогда
.
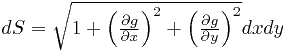Выполняется замена в подынтегральной функции, и поверхностный интеграл сводится к двойному:
,
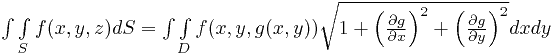где 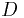- область плоскости 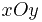, в которую проектируется часть поверхности, по которой проводится интегрирование.

Однако часто задать поверхность явным уравнением невозможно, и тогда она задаётся параметрически, т.е. уравнениями вида
.
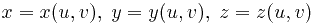Элемент поверхности в этом случае записывается уже сложнее:
.
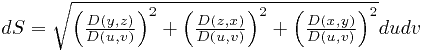Соответствующим образом записывается и поверхностный интеграл:
,
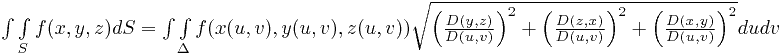где 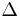- область изменения параметров, соответствующая части поверхности 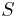, по которой проводится интегрирование.

5. Физический смысл криволинейного и поверхностного интегралов первого рода

Обсуждаемые интегралы обладают очень простым и наглядным физическим смыслом. Пусть имеется некоторая кривая, линейная плотность которой не является
константой, а представляет собой функцию точки 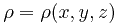. Найдём массу этой кривой. Разобьём кривую на множество малых элементов,
в пределах которых её плотность можно приближённо считать константой. Если длина маленького кусочка кривой равна 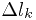, то его масса
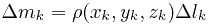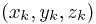, где - любая точка выбранного кусочка кривой (любая, так как плотность в пределах
этого кусочка приближённо предполагается постоянной). Соответственно, масса всей кривой получится суммированием масс отдельных её частей:
.
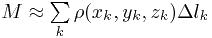Чтобы равенство стало точным, следует перейти к пределу разбиения кривой на бесконечно малые части, но это и есть криволинейный интеграл первого рода.

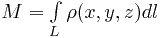
Аналогично разрешается вопрос о полном заряде кривой, если известна линейная плотность заряда .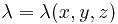

Эти рассуждения легко переносятся на случай неравномерно заряженной поверхности с поверхностной плотностью заряда 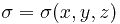. Тогда
заряд поверхности есть поверхностный интеграл первого рода
.

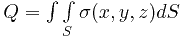Замечание. Громоздкая формула для элемента поверхности, заданной параметрически, неудобна для запоминания. Другое выражение получается в дифференциальной геометрии,
оно использует т.н. первую квадратичную форму поверхности.

Примеры вычисления криволинейных интегралов первого рода

Пример 1. Интеграл вдоль прямой.
Вычислить интеграл

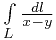
вдоль отрезка прямой, проходящей через точк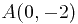и и .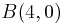

Сначала запишем уравнение прямой, вдоль которой проводится интегрирование: 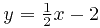. Найдём выражение для :
.
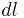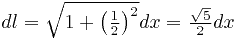Вычисляем интеграл:

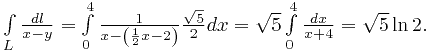
Пример 2. Интеграл вдоль кривой на плоскости.
Вычислить интеграл

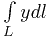
по дуге параболы 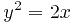от точки 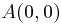до точки .

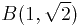Заданные точк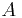и и 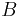позволяют выразить переменную 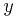из уравнения параболы: .

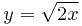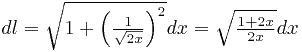
Вычисляем интеграл:
.

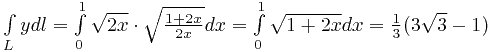Однако можно было проводить вычисления и иначе, пользуясь тем, что кривая задана уравнением, разрешённым относительно переменной .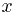
Если принять переменную 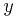за параметр, то это приведёт к небольшому изменению выражения для дифференциала дуги:
.
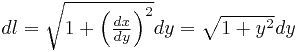Соответственно, интеграл несколько изменится:
.
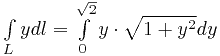Этот интеграл легко вычисляется подведением переменной под дифференциал. Получится такой же интеграл, как и в первом способе вычисления.

Пример 3. Интеграл вдоль кривой на плоскости (использование параметризации).
Вычислить интеграл

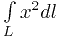
вдоль верхней половины окружности .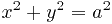

Можно, конечно, выразить из уравнения окружности одну из переменных, а затем провести остальные вычисления стандартно. Но можно использовать и
параметрическое задание кривой. Как известно, окружность можно задать уравнениями 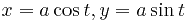. Верхней полуокружности
отвечает изменение параметра в пределах 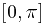. Вычислим дифференциал дуги:
.
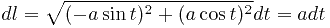Таким образом,

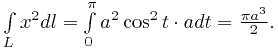
Пример 4. Интеграл вдоль кривой на плоскости, заданной в полярных координатах.
Вычислить интеграл

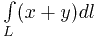
вдоль правого лепестка лемнискаты .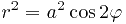

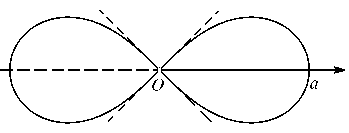
На чертеже выше изображена лемниската. Вдоль её правого лепестка нужно проводить интегрирование. Найдём дифференциал дуги для кривой :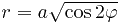
.
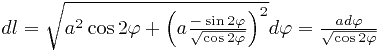Следующий шаг - определение пределов интегрирования по полярному углу. Ясно, что должно выполняться неравенство 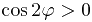, а потому
.
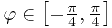Вычисляем интеграл:

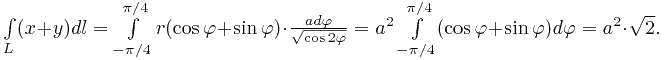
Пример 5. Интеграл вдоль кривой в пространстве.
Вычислить интеграл

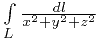
вдоль витка винтовой линии 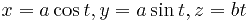, соответствующего пределам изменения параметра .

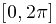Вычисляем дифференциал дуги:
.
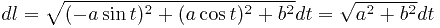Подставляем в интеграл:
.

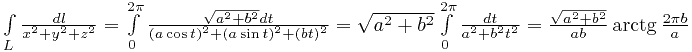Примеры вычисления поверхностных интегралов первого рода

Пример 6. Интеграл по поверхности, заданной явно.
Вычислить интеграл

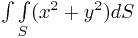
по поверхности тела .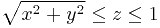

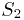Поверхность интегрирования состоит из двух частей: части плоскости , которую обозначим и поверхности 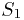, заданной
уравнением 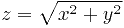. Эта поверхность представляет собой верхнюю половину конуса второго порядка. Проекция той её части,
по которой проводится интегрирование, на плоскость 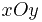представляет собой круг, ограниченный окружностью .
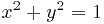Запишем элемент поверхности:
.
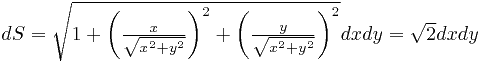Таким образом, поверхностный интеграл сводится к следующему двойному:

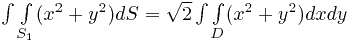
где 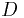- круг 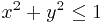. Такой интеграл проще всего вычислять в полярных координатах:
.

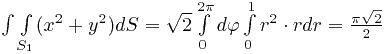Теперь интегрируем по плоскости . Это совсем простое интегрирование, так как поверхностный интеграл сразу превращается
в двойной без каких-либо дополнительных вычислений. Он будет отличаться только множителем 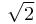от только что вычисленного.

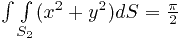
Окончательный ответ получается суммированием двух вычисленных интегралов:
.

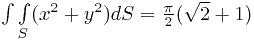Пример 7. Интеграл по сфере.
Вычислить интеграл

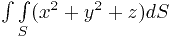
по верхней полусфере .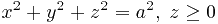

Можно выразить явно, например, аппликату из уравнения сферы и проводить вычисления дальше, но при интегрировании по сфере удобно использовать
сферические координаты. Тем более элемент поверхности сферы в этом случае хорошо известен:
.
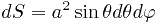Осталось только выполнить замену в подынтегральной функции:
.

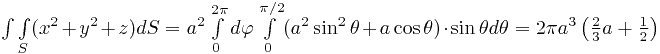Пример 7. Интеграл по параметрически заданной поверхности.
Вычислить интеграл

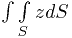
по части поверхности геликоида 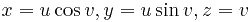, отвечающей границам изменения параметров .

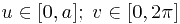Поверхность интегрирования задана параметрически, поэтому для написания элемента поверхности нужно предварительно вычислить три якобиана:

.
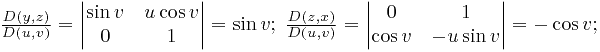
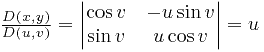Таким образом, элемент поверхности
.
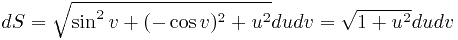Следовательно, поверхностный интеграл сводится к следующему двойному:
.
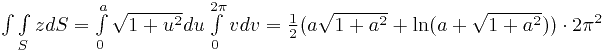Детали вычисления определённого интеграла здесь опущены: они не имеют отношения к теме. Тем более, сам интеграл достаточно простой.

8.Теория Поля.

Теория поля немецкого психолога Курта Левина (1890-1947) сложилась под влиянием успехов точных наук - физики, математики. Начало века ознаменовалось открытиями в физике поля, атомной физике, биологии. Заинтересовавшись в университете психологией, Левин пытался и в эту науку внести точность и строгость эксперимента, сделав ее объективной и экспериментальной.

Теория Курта Левина является оригинальной теорией в объяснении человеческого поведения. Согласно ей, протекание действий целиком сводится к конкретной совокупности условий существующего в данный момент поля. Свою теорию личности Левин разрабатывал в русле гештальтпсихологии, дав ей название «теория психологического поля». Он исходил из того, что личность живет и развивается в психологическом поле окружающих ее предметов, каждый из которых имеет определенный заряд (валентность). Эксперименты Левина доказывали, что для каждого человека эта валентность имеет свой знак, хотя в то же время существуют такие предметы, которые для всех имеют одинаково притягательную или отталкивающую силу. Воздействуя на человека, предметы вызывают в нем потребности, которые Левин рассматривал как своего рода энергетические заряды, вызывающие напряжение человека. В этом состоянии человек стремится к разрядке, т.е. удовлетворению потребности.

В рамках теории поля Курт Левин предлагает схему психологического изучения человеческого поведения, которая имеет целый ряд отличительных особенностей:

1. Согласно ей, анализ поведения должен основываться на общей ситуации. В объяснение поведения включается более широкий круг явлений, чем объединение отдельных элементов типа раздражителей и реакций.

2. Ситуацию следует интерпретировать так, как она представляется субъекту. Это означает, что объяснение должно быть психологичным. При этом детерминанты поведения независимо от локализации в окружении или субъекте должны пониматься психологически. В связи с этим к основным компонентам причинно-следственного анализа относятся, например, не раздражители, как это пытается доказать бихевиоризм, а воспринимаемые (отраженные субъектом) особенности окружения, которые предоставляют человеку различные возможности для действия. Психологическому анализу должно подлежать таким образом не только все, что происходило с действующим субъектом в нем самом и окружении, но и другие факторы, влияющее на поведение.

3. Для объяснения поведения описания простых связей в смысле ассоциации «раздражитель-реакция» явно недостаточно. Согласно Курту Левину, в основе всякого поведения лежат силы, основными из которых являются потребности.

4. Простая классификация наблюдаемых феноменов не идет дальше описательного уровня и может стать причиной неверного объяснения, поскольку внешне одинаковое поведение не обязательно связано с одними и теми же причинами. Необходимо выработать общие понятия и использовать их как конструктивные элементы, сочетание которых позволяло бы объяснить каждый конкретный случай.

5. На поведение влияет только то, что действует здесь и теперь: будущие и прошлые события сами по себе не могут определять поведение в настоящий момент, они действенны лишь как нечто актуально припоминаемое или предвосхищаемое. Прошлые и будущие события могут лишь внести свой вклад в структуру общей ситуации и несколько изменить композицию поля, но не более. Но, тем ни менее, их влияние может сказываться на актуальных состояниях субъекта и его окружения.

В своей модели психологического объяснения поведения Курт Левин стремился осуществить анализ условий протекания явлений и свести их к основным объяснительным конструктам. Конструктами стати понятия общей динамики, такие, как напряжение, сила, поле (по аналогии с электромагнитным и гравитационным полями).Еще более значительным для исследования поведения было требование Левина анализировать ситуацию в целом. Результатом такого требования анализа стало знаменитое уравнение поведения, согласно которому поведение (В) есть функция личностных факторов (Р) и факторов окружения (Е): B = f(P,E).Исходя из этого, для объяснения поведения Левин разработал две отчасти дополняющие друг друга модели:

- личности;

- окружения.

Структурными компонентами этих моделей являются соседствующие, отграниченные друг от друга области. Несмотря на это сходство, структурные области в каждой из моделей имеют разное значение, которое определяется прежде всего динамическими компонентами обеих моделей.Модель личности оперирует энергиями и напряжениями, т.е. скалярными величинами.Модель окружения имеет дело с силами и целенаправленным поведением (в сфере действия соответствует локомоциям), т.е. векторными величинами. В конечном счете обе теоретические схемы базируются на представлении гомеостатической регуляции: создавшееся положение стремится к состоянию равновесия между различными областями пространственного распределения напряжений, или сил. При этом регулирующим принципом является не уменьшение напряжения, а его уравновешивание по отношению к более общей системе или полю в целом.

К основным понятиям теории поля относятся:

- Жизненное пространство. Жизненное пространство является ключевым понятием в теории поля Курта Левина. Содержание этого термина включает в себя все множество реальных и нереальных, актуальных, прошлых и будущих событий, которые находятся в психологическом пространстве индивида в данный момент времени. Это могут быть ожидания, цели, образы притягательных (или отталкивающих) объектов, реальные или воображаемые преграды на пути достижения желаемого, деятельность человека и т.д. В общем, все, что может обусловить поведение личности. Исходя из этого, поведение - это функция личности и ее жизненного пространства в данный момент времени. Существенно отметить, что Левин признавал наличие влияния не психических событий на поведение человека. Поэтому даже неосознаваемые человеком влияния, связанные с социально-экономическими и физиологическими факторами, также включаются в анализ его жизненного пространства. Иногда жизненное пространство называют психологическим.

- Регионы и границы. Психологическое пространство состоит из разных секторов, регионов, которые графически изображаются разделенными границами. Границы обладают свойством проницаемости. Чем «жестче» граница, барьер, тем толще линия, ее изображающая. Факт жизненного пространства — все, что может быть осознано человеком. Событие — результат взаимодействия нескольких фактов. Количество секторов, регионов определяется количеством фактов, находящихся в данный момент в жизненном пространстве. Чем ближе сектор к личному пространству человека, тем большее влияние он оказывает.

- Локомоции. Связь между регионами осуществляется посредством локомоций. Локомоции (действия) могут происходить как в реальном физическом пространстве, так и в нереальном, воображаемом. Функция локомоций заключается в регуляции напряжения в жизненном пространстве человека. Уровень напряжения одного сектора может регулироваться за счет осуществления локомоций в другом секторе. Например, мечты могут являться ирреальными локомоциями, связанными с регуляцией напряжения, вызванного потребностями, которые в данный момент времени невозможно удовлетворить в физическом пространстве. Если мечты не снижают напряжения, человек задействует для разрядки другие регионы. Если локомоции в доступных человеку регионах не снижают уровень напряжения, а остальные регионы характеризуются жесткостью границ «на входе», то поведение человека может описываться как навязчивое. Когда мы выводим событие, например локомоцию... из жизненного пространства, необходимо следовать трем принципам.

- Принцип связности (событие - всегда результат взаимодействия двух и более фактов).

- Принцип конкретности (эффект могут иметь только конкретные факты. Конкретный факт - это актуально существующий в жизненном пространстве факт).

- Принцип одновременности (лишь факты настоящего могут продуцировать поведение в настоящем).

Временная перспектива. Курт Левин поставил вопрос о существовании единиц психологического времени различного масштаба, обусловленного масштабами жизненных ситуаций, определяющих границы «психологического поля в данный момент». Это поле включает в себя не только настоящее положение индивида, но и его представления о своем прошлом и будущем - желания, страхи, мечты, планы и надежды. Все части поля, несмотря на их хронологическую разновременность, субъективно переживаются как одновременные и в равной мере определяют поведение человека. Эта точка зрения стимулировала исследования временной перспективы личности. В своей статье «Определение понятия „поле в данный момент"» Курт Левин определяет временную перспективу как феномен, «включающий психологическое прошлое и будущее на реальном и различных ирреальных уровнях» (Левин К., 1980). Сам же термин «временная перспектива» был введен в науку Л. Франком в 1939 году для характеристики взаимосвязи и взаимообусловливания прошлого, настоящего и будущего в сознании и поведении человека.

Валентность. Еще один конструкт, используемый Куртом Левиным для анализа психических феноменов и входящий в понятийный аппарат теории поля, это валентность. Под валентностью понимается свойство объекта притягивать или отталкивать. То есть речь идет о ценности региона для человека. Притягательный регион имеет положительную валентность, а отталкивающий — отрицательную. Есть регионы, которые имеют для человека нейтральную валентность.

Напряжение, существующее в психологическом пространстве человека, обусловливает силу, действующую на него и направленную в регион, который призван уровень напряжения понизить. Если на человека действуют несколько сил, то его локомоции направлены в сторону их результирующей. На рисунках, как это принято в физике, сила обозначается вектором. «Сила, или «тенденция к передвижению», имеет концептуально иной характер, чем действительное передвижение, хотя передвижение - это один из признаков (операциональное определение) для констелляции сил...». Сила обусловлена величиной валентности, присущей объекту в данный момент времени.

Скалярные и векторные поля

Скалярное поле

Скалярным полемназывается часть пространства, каждой точке которого поставлена в соответствие определённое число –скаляр.

Примеры скалярных полей: 1) поле температур внутри неоднородно нагретого тела; 2) поле давлений воздуха в атмосфере; 3) поле плотности вещества в теле; 4)поле плотности распределения электрического заряда и т.д.

Скалярное поле считается заданным, если в каждой точке M некоторой области W определена скалярная функция U(M). В связи с этим, понятие скалярного поля и функции, определенной в области W, эквивалентны. Если скалярное поле отнесено к декартовой системе координат, то скалярную функцию U(M) можно записать, например, в виде функции двух U(x,y) или трёх U(x,y,z) переменных.

Простейшей геометрической характеристикой скалярного поля U(M) являются поверхности уровня.

Поверхности уровня – это геометрическое место точек, в которых скалярная функция принимает постоянные значения, т.е.U(x,y,z)=C, гдеС – произвольная постоянная.

В случае двумерного поля понятие поверхности уровня заменяется понятием линии уровня: U(x,y)=C.

П

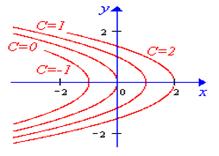
Рис. 1.1

Примеры линий уровня: 1) на топографических картах линии, соединяющие точки, имеющих одну и туже высоту над уровнем моря; 2) в термодинамике на диаграммах состояния линии, соединяющие точки, имеющих одну и туже температуру (изотермы), давление (изобары) или объём (изохоры); 3) в электростатике линии, соединяющие точки, имеющие одинаковый потенциал (эквипотенциальные линии).

Пример 1.1. Изобразить линии уровня скалярного поля U(x,y)=y2+x.

Решение. Записываем y2+x=С y2=C–x. Это есть семейство парабол (см. рис.1.1).

Векторное поле

Векторным полем называется часть пространства, каждой точке которого поставлен в соответствие определённый вектор.

Примеры векторных полей:

1) поле скоростей текущей жидкости;
2) силовые поля: электрическое, магнитное, гравитационное.

Векторное поле считается заданным, если в каждой его точке М определена векторная функция 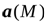. Если векторное поле отнесено к декартовой системе координат, то векторную функцию можно записать в виде:

.

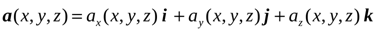Простейшей геометрической характеристикой векторного поля являются векторные линии.

Векторные линии – это линии, в каждой точке которой касательная имеет направление соответствующего ей вектора.

Примеры векторных линий: 1) если рассматривается поле скоростей текущей жидкости, то векторные линии суть линии тока этой жидкости, т.е. траектории движения частиц жидкости; 2) для геометрического представления магнитного поля используются магнитные силовые линии (для экспериментального изображения магнитных силовых линий используют металлические опилки, насыпанные на лист бумаги, в магнитном поле эти опилки выстраиваются вдоль силовых линий).

Замечание. Наряду с понятием векторной линией, часто используется также и понятие векторной трубки. Векторной трубкойназывается поверхность, образованная векторными линиями, проходящими через точки некоторой лежащей в поле замкнутой кривой, не совпадающей (даже частично) с какой-либо векторной линией.

В вопросах, связанных с изучением полей важную роль играет задача о нахождении векторной линии поля 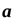, проходящей через заданную точку M. Пусть уравнение векторной линии имеет вид

, ,

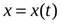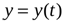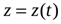
или в векторной форме

.

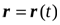По условию в каждой точке этой линии вектор поля 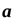направлен по касательной к ней. Из геометрического смысла производной известно, что производная любой функции определяет направление касательной к этой функции. Поэтому, производная 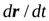направлена по касательной к векторной линии. Следовательно, векторы 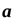и 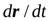– коллинеарны. Два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны. В результате получаем

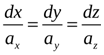(1.1)

Это есть система дифференциальных уравнений для нахождения уравнений векторных линий.
ПРИМЕР 1.2. Найти уравнение векторных линий векторного поля

.

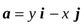Решение. Для двухмерных полей система дифференциальных уравнений векторных линий принимает вид

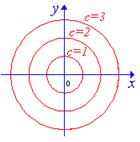
Рис. 1.2

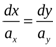
В данном случае ; 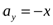. Поэтому

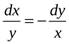
Разделяя переменные и интегрируя, получим

.

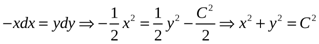Таким образом, векторные линии представляют собой совокупность окружностей (см. рис. 1.2).

Теория вероятности.

Тео́риявероя́тностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей[1]. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год)[2].

Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний. В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышёв, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова. Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.

Теория вероятностей изучает объективные закономерности массовых случайных событий. Она является теоретической базой для математической статистики, занимающейся разработкой методов сбора, описания и обработки результатов наблюдений. Путем наблюдений (испытаний, экспериментов), т.е. опыта в широком смысле слова, происходит познание явлений действительного мира.

В своей практической деятельности мы часто встречаемся с явлениями, исход которых невозможно предсказать, результат которых зависит от случая.

Случайное явление можно охарактеризовать отношением числа его наступлений к числу испытаний, в каждом из которых при одинаковых условиях всех испытаний оно могло наступить или <