Раздел iii. электростатика. постоянный ток
3.1. ОСНОВНЫЕ ФОРМУЛЫ (В ЕДИНИЦАХ СИ)
1. Закон Кулона 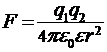 ;
;
2. Напряжённость электростатического поля 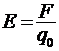 ;
;
3. Напряжённость поля точечного заряда 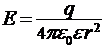 ;
;
4. Напряжённость поля бесконечно длинной заряженной нити 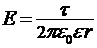 ;
;
5. Напряжённость поля равномерно заряженной плоскости 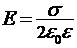 ;
;
6. Напряжённость поля между двумя равномерно и разноимённо заряженными бесконечно параллельными плоскостями 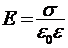 ;
;
7. Напряжённость поля E создаваемого металлической заряженной сферой радиуса R на расстоянии r от центра сферы
а) на поверхности сферы (r = R) 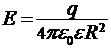 ;
;
б) вне сферы (r > R) 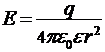 ;
;
8. Смещение электрического поля 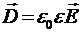 ;
;
9. Работа перемещения электрического заряда в электрическом поле из точки A в точку B 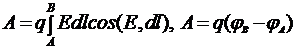 ;
;
10. Потенциал поля точечного заряда 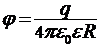 ;
;
11. Потенциал поля металлической полой сферы:
а) на поверхности и внутри сферы 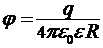 ,
,
б) вне сферы (r > R) 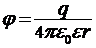 .
.
12. Связь между напряжённостью поля и градиентом потенциала 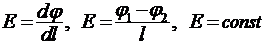 ;
;
13. Сила натяжения между двумя разноимёнными заряженными обкладками конденсатора 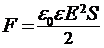 ;
;
14. Электрическая емкость уединённого проводника 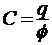 ;
;
15. Емкость плоского конденсатора 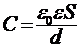 ;
;
16. Емкость слоистого конденсатора 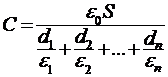 ;
;
17. Емкость батареи параллельно соединённых конденсаторов 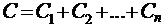 ;
;
18. Формула для определения ёмкости батареи последовательно соединённых конденсаторов 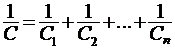 ;
;
19. Энергия заряженного проводника 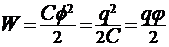 ;
;
20. Энергия заряженного плоского конденсатора 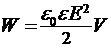 ;
;
21. Объёмная плотность энергии электрического поля 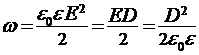 ;
;
22. Сила тока 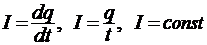 ;
;
23. Плотность тока 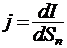 ;
;
24. Закон Ома для участка цепи, не содержащего ЭДС 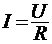 ;
;
25. Закон Ома для полной цепи 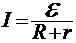 , где
, где 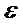 - ЭДС;
- ЭДС;
26. Закон Ома в дифференциальной форме 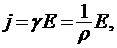
E – напряжённость электрического поля, 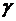 - электропроводность,
- электропроводность, 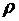 - удельное сопротивление;
- удельное сопротивление;
27. Закон Джоуля – Ленца 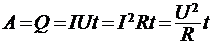 ;
;
28. Закон Джоуля – Ленца в дифференциальной форме 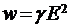 ;
;
29. Термоэлектродвижущая сила 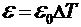 ;
;
30. Сопротивление однородного проводника 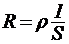 ;
;
31. Удельная проводимость (электропроводность) 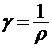 ;
;
32. Зависимость удельного сопротивления от температуры 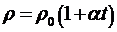 ;
;
33. Полная мощность, выделяющаяся в цепи 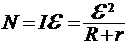 ;
;
34. Коэффициент полезного действия источника тока 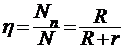 ;
;
35. Законы Кирхгофа
а) первый 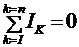 ,
,
б) второй 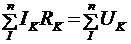 ;
;
36. Работа выхода 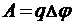 ;
;
37. Формула Ричардсона – Дешмана (удельная эмиссия): 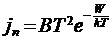 , где B – постоянная, e – основание натуральных алгоритмов;
, где B – постоянная, e – основание натуральных алгоритмов;
38. Плотность тока в газе: 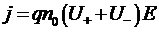 ;
;
39. Удельная собственная проводимость полупроводников 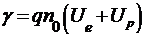 ;
;
40. Зависимость удельной собственной проводимости полупроводников от температуры T: 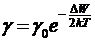 ,
,
где 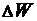 - ширина запрещённой зоны;
- ширина запрещённой зоны;
41. Первый закон Фарадея для электролиза 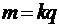 ;
;
42. Второй закон Фарадея для электролиза 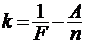 .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. В вершинах квадрата расположены равные положительные заряды 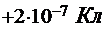 (рис.1). В центр квадрата помещен отрицательный заряд. Вычислить, какой величины должен быть этот заряд, чтобы уравновесить силу взаимного отталкивания зарядов, расположенных по вершинам квадрата.
(рис.1). В центр квадрата помещен отрицательный заряд. Вычислить, какой величины должен быть этот заряд, чтобы уравновесить силу взаимного отталкивания зарядов, расположенных по вершинам квадрата.
Дано: 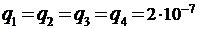 Кл.
Кл.
Найти: 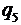
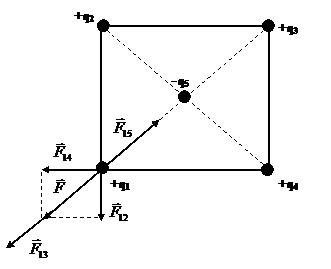

Рис. 1
Решение: Для определения величины q5 используем закон Кулона. Заряды q1 , q2 , q3 , q4 одинаковы и расположены симметрично. Определим условия, при которых один из зарядов, например 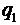 , находился бы в равновесии с зарядом
, находился бы в равновесии с зарядом 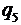 . Устанавливаем силы отталкивания, которые испытывает заряд q1 от положительных зарядов q2 , q3 , q4. По принципу суперпозиции поле каждого заряда q2 , q3 , q4 действует на заряд
. Устанавливаем силы отталкивания, которые испытывает заряд q1 от положительных зарядов q2 , q3 , q4. По принципу суперпозиции поле каждого заряда q2 , q3 , q4 действует на заряд 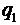 независимо. Это позволяет составить векторную сумму этих сил
независимо. Это позволяет составить векторную сумму этих сил 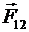 ,
, 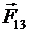 ,
, 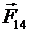 . Чтобы выполнить условие равновесия зарядов
. Чтобы выполнить условие равновесия зарядов 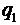 и
и 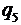 , надо, чтобы векторная сумма действующих сил была равна нулю. С учетом сказанного:
, надо, чтобы векторная сумма действующих сил была равна нулю. С учетом сказанного:
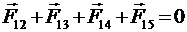 , (1)
, (1)
где 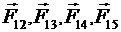 - силы, действующие со стороны зарядов q2 , q3 , q4. и
- силы, действующие со стороны зарядов q2 , q3 , q4. и 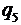 на заряд
на заряд 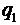 . Учитывая расположение зарядов (см. рис.1) заменим в (1)
. Учитывая расположение зарядов (см. рис.1) заменим в (1) 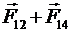 на
на 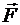 и получим:
и получим:
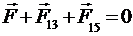 . (2)
. (2)
Переходим от векторного к скалярному выражению, здесь 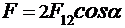
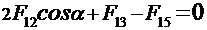 . (3)
. (3)
Определяем величину заряда, применяя закон Кулона:
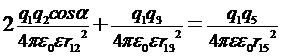 .
.
Так как 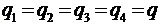 , то
, то
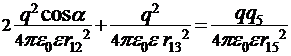 . (4)
. (4)
Кроме того, по условию 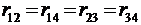 , тогда
, тогда
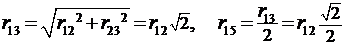 . (5)
. (5)
Подставляя в (4) 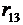 и
и 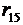 из (5), после преобразования получим:
из (5), после преобразования получим:
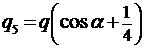 .
.
Производим вычисления в единицах СИ:
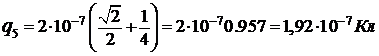 .
.
Пример 2. Два одинаковых положительных заряда 10-7 Кл находятся в воздухе на расстоянии 8 см друг от друга. Определить напряженность в точке О, находящейся на середине отрезка, соединяющего заряды, и в точке А, расположенной на расстоянии 5 см от зарядов.
Дано: 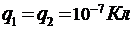 ,
, 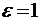 , 2r= 8 см = 0,08 м, r1 = 0,05 м. Найти Е0 и Е.
, 2r= 8 см = 0,08 м, r1 = 0,05 м. Найти Е0 и Е.
Решение: Напряженность поля, создаваемого зарядами, находится по принципу суперпозиции. Результирующая напряженность Е определяется векторной суммой напряженностей, создаваемых каждым зарядом в данной точке поля:
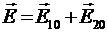 , (1)
, (1)
где 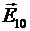 и
и 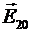 - величины напряженностей полей, определяемых по формуле
- величины напряженностей полей, определяемых по формуле
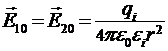 . (2)
. (2)
Чтобы найти числовые значения напряженности в точке О, надо сначала построить векторы напряженностей 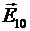 и
и 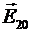 . Т.к. заряды положительные, их векторы направлены от точки О в сторону от зарядов, создающих это поле (рис.2)
. Т.к. заряды положительные, их векторы направлены от точки О в сторону от зарядов, создающих это поле (рис.2)
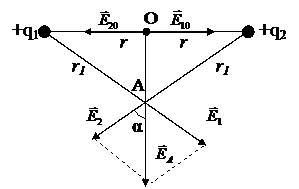

Рис. 2
Кроме того, заряды равны и расположены на равном расстоянии от точки О. Поэтому с учетом направления векторов из формулы (1) следует:
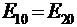 ,
, 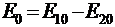 , отсюда получаем
, отсюда получаем 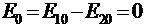 .
.
В точке А напряженность вычисляется по формуле (1) при аналогичном построении векторов. Результирующий вектор напряженности 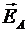 является диагональю параллелограмма (см. рис.2), следовательно,
является диагональю параллелограмма (см. рис.2), следовательно, 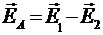 или
или 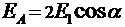 , т.к.
, т.к. 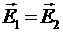 .Численное значение напряженности поля в точке А определяется по формуле
.Численное значение напряженности поля в точке А определяется по формуле
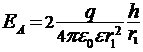 ,
,
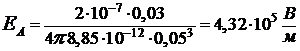 , h = OA = 0,03 м.
, h = OA = 0,03 м.
Проверяем единицу измерения: 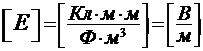 .
.
Пример 3. Установить, как изменится емкость и энергия плоского воздушного конденсатора, если параллельно его обкладкам ввести металлическую пластину толщиной 1 мм. Площадь обкладки конденсатора и пластины 150 см2, расстояние между обкладками 6 мм. Конденсатор заряжен до 400 В и отключен от батареи.
Дано: 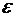 = 1,
= 1, 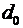 = 1 мм = 10-3 м, S = 150 см2 =
= 1 мм = 10-3 м, S = 150 см2 = 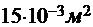 , d = 6 мм =
, d = 6 мм = 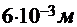 , U = 400 В.
, U = 400 В.
Найти: 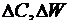 .
.
Решение: Емкость и энергия конденсатора при внесении в него металлической пластины будут изменяться. Это вызвано тем, что уменьшается расстояние между пластинами от d до d-d0 (рис.3). Используем формулу электроемкости плоского конденсатора.
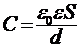 , (1)
, (1)
где S - площадь пластины, d - расстояние между пластинами.
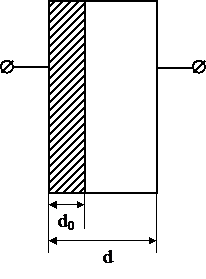

Рис.3.
В нашем случае
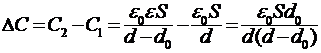 . (2)
. (2)
Проводим вычисления в системе СИ:
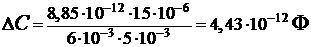 .
.
Проверим единицу измерения СИ:
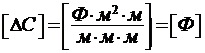 .
.
Так как электрическое поле в плоском конденсаторе однородно, плотность энергии во всех его точках одинакова и равна 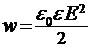 , где Е - напряженность поля между обкладками. При внесении металлической пластины параллельно обкладкам напряженность поля остается неизменной, а объем электрического поля уменьшился на
, где Е - напряженность поля между обкладками. При внесении металлической пластины параллельно обкладкам напряженность поля остается неизменной, а объем электрического поля уменьшился на
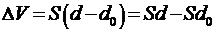 .
.
Следовательно, изменение энергии (конечное значение меньше начального) произошло вследствие уменьшения объема поля конденсатора:
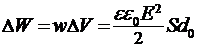 . (3)
. (3)
Напряженность поля Е определяется через градиент потенциала
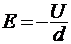 , (4)
, (4)
где U - разность потенциалов, d - расстояние между обкладками. Расчетная формула (3) с учетом формулы (4) примет вид:
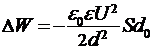 . (5)
. (5)
Подставляя числовые значения (в единицах СИ) в формулу (5), получаем:
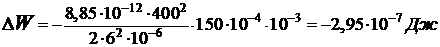 .
.
Проверяем единицу измерения:
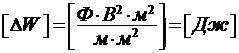 .
.
Пример 4. Плоский воздушный конденсатор из двух пластин, расположенных на расстоянии 4 мм друг от друга, общей площадью 100 см2. Конденсатор заряжают от батареи в 200 В и отключают от нее. Какую работу нужно совершить, чтобы увеличить расстояние между обкладками в два раза? Решить задачу при условии, когда конденсатор не отключают от батареи.
Дано: 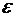 = 1,
= 1, 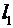 = 4 мм =
= 4 мм = 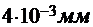 , S1= S2 = 50 см2=
, S1= S2 = 50 см2= 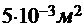 ,
, 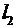 = 8 мм =
= 8 мм = 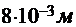 , U0 = 200 В.
, U0 = 200 В.
Найти: А.
Решение: Чтобы увеличить расстояние между обкладками конденсатора, отключенного от батареи, необходимо совершить работу под действием внешних сил. Работа внешних сил 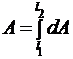 зависит от приложенной силы F и перемещения от
зависит от приложенной силы F и перемещения от 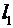 до
до 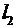 , где
, где
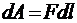 . (1)
. (1)
Приложенная сила определяется силой взаимодействия между пластинами
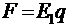 , (2)
, (2)
где q - заряд пластины, E1 - напряженность поля одной пластины. Величина напряженности может быть получена через градиент потенциала
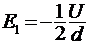 . (3)
. (3)
Заряд пластины, перемещаемый относительно другой пластины, может быть найден по площади пластины S, расстоянию между обеими пластинами l и разности потенциалов U. Из формулы емкости плоского конденсатора 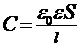 ,
, 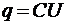 получаем
получаем
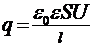 . (4)
. (4)
Проведя подстановку формул (2-4) в уравнение (1), получаем
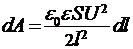 . (5)
. (5)
Для определения полной работы необходимо учесть, что при отключенном конденсаторе напряжение изменяется, но заряд q и напряженность поля Е остаются неизменными:
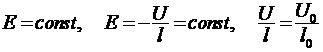 . (6)
. (6)
Подставим выражение (6) в уравнение (5) и проинтегрируем:
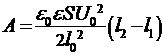 . (7)
. (7)
Подставляя в (7) числовые значения (в единицах СИ, находим)
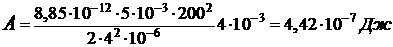 .
.
Пример 5. Найти токи, протекающие в каждой ветви электрической цепи (рис. 4), если 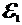 = 130 В,
= 130 В, 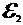 = 117 В, R
= 117 В, R 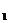 = 0,5 Ом, R
= 0,5 Ом, R 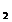 = 0,3 Ом, R
= 0,3 Ом, R 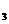 = 12 Ом. Внутреннее сопротивление источников ЭДС не учитывать.
= 12 Ом. Внутреннее сопротивление источников ЭДС не учитывать.
Дано: 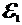 = 130 В,
= 130 В, 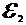 = 117 В, R
= 117 В, R 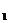 = 0,5 Ом, R
= 0,5 Ом, R 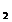 = 0,3 Ом, R
= 0,3 Ом, R 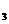 = 12 Ом.
= 12 Ом.
Найти 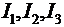
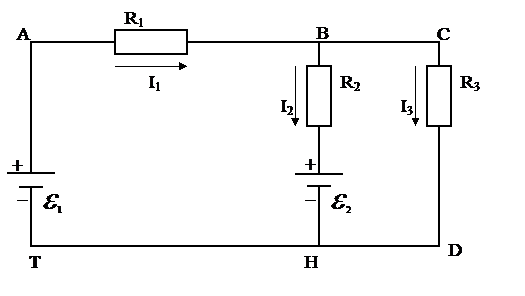

Рис.4.
Решение: Задача дана для расчета разветвленных цепей, когда в них есть несколько источников тока. При решении задач такого типа рационально пользоваться законами (правилами) Кирхгофа. Первый закон сформулирован для узлов, т.е. точек разветвления цепи, в которых сходится больше двух проводников: алгебраическая сумма токов, сходящихся в узле равна нулю 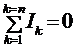 .
.
Второй закон для замкнутых контуров гласит: в любом замкнутом контуре алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС в контуре 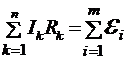 .
.
Решая совместно составленные по этим правилам уравнения, можно определить ту или иную искомую величину (сопротивления внешней цепи или силы токов, ЭДС). Для составления уравнений по указанным законам надо придерживаться следующих правил:
1. Обозначить на схеме буквами узлы и контуры.
2. Произвольно выбрать направление токов (если они не оговорены условием задачи) во всех участках цепи и обозначить их на чертеже стрелками.
3. Учесть направление токов при составлении уравнения по первому закону. Положительными считать токи, подходящие к узлу, отрицательными - отходящие от узла.
4. Составить систему уравнений для первого закона Кирхгофа. Число уравнений, составленных по этому правилу, должно быть на единицу меньше числа узлов в цепи.
5. Выбрать произвольно направление обхода контура. Условиться, что ЭДС в уравнении будет положительна, если направление от положительного полюса к отрицательному вне источника тока совпадает с направлением обхода, в противном случае ЭДС отрицательна.
6. Считать падение напряжения в цепи положительным, если выбранное ранее направление тока на этом участке (между двумя узлами) совпадает с направлением обхода контура, и отрицательным, если направление тока не совпадает с направлением обхода контура.
7. Первый контур выбирается произвольно. При составлении уравнений для следующих контуров надо включать в них контуры, ранее не входившие.
8. Число уравнений, составленных по второму закону Кирхгофа, определяется следующим условием. Если число контуров в цепи m , а узлов в ней n , то число независимых уравнений, достаточных для решения, равно m - n+1.
9. Получение в ответе токов с отрицательными знаками означает только то, что было выбрано направление, обратное действительному.
Согласно сформулированным выше правилам, решаем задачу 5:
1) Обозначим на схеме контуры, узлы, направления токов.
2) Устанавливаем m - число ветвей (в данной схеме их 3) и n - число узлов (в данной схеме их 2 - в точках В и Н, (см. рис.4).
3) Для составления уравнения по первому закону Кирхгофа следует выбрать один из указанных узлов. Выбираем узел В, в котором сходятся токи трех проводников. Учитывая направление токов, получим
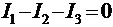 . (1)
. (1)
4) Устанавливаем число уравнений, необходимых для решения задач по второму закону Кирхгофа. Это число уравнений равно m - n+1 = 3 – 2 + 1 = 2. Выбираем контуры ВСДНВ и АВНТА. Устанавливаем обход по контуру ВСДНВ. Учитывая правило знаков, выбираем обход по часовой стрелке, при котором ЭДС 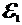 будет положительной. С учетом выбранного ранее направления токов составляем первое уравнение по второму закону Кирхгофа
будет положительной. С учетом выбранного ранее направления токов составляем первое уравнение по второму закону Кирхгофа
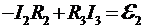 . (2)
. (2)
Составляем уравнение для второго контура. Для этого устанавливаем направление обхода для контура А В Н Т А. Так как в этом контуре два источника тока и 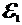 больше
больше 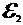 , обход начинаем от
, обход начинаем от 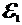 к
к 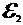 по часовой стрелке. Кроме этого, знаки при ЭДС и падении напряжения (IR) устанавливаем в соответствии с ранее записанными правилами
по часовой стрелке. Кроме этого, знаки при ЭДС и падении напряжения (IR) устанавливаем в соответствии с ранее записанными правилами
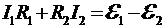 . (3)
. (3)
Из уравнения (1) находим
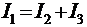 . (4)
. (4)
Для определения числовых результатов подставляем в формулу (2) и (3) известные числовые значения сопротивления и ЭДС.
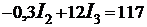 , (5)
, (5)
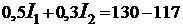 . (6)
. (6)
После сложения (5) и (6) получим
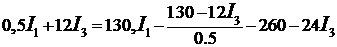 . (7)
. (7)
Подставляя полученную силу тока 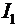 в (4), находим
в (4), находим
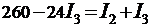 .
.
Следовательно
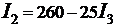 .(8)
.(8)
Силу тока 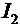 (8) используем в выражении (5):
(8) используем в выражении (5):
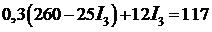 ,
,
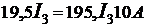 . (9)
. (9)
Зная I3 из формулы (7), находим
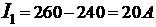 . (10)
. (10)
Определяем значение I2 из выражения (4)
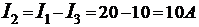 .
.
Задача 6. Найти сопротивление железного стержня диаметром 1 мм, если масса этого стержня 1 кг.
Решение. Сопротивление стержня можно рассчитать по формуле 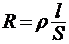 ,
,
где R - сопротивление, 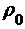 - удельное сопротивление. l - длина стержня, S – площадь поперечного сечения стержня.
- удельное сопротивление. l - длина стержня, S – площадь поперечного сечения стержня.
Площадь сечения круглого стержня определяется 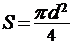 , где d - диаметр стержня. Длина стержня выразится из его массы:
, где d - диаметр стержня. Длина стержня выразится из его массы: 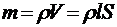 , где m - масса стержня,
, где m - масса стержня, 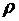 - удельная плотность материала стержня, V - объем стержня,
- удельная плотность материала стержня, V - объем стержня, 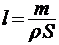 . Подставив найденные значения S и l в формулу для R. получим:
. Подставив найденные значения S и l в формулу для R. получим:
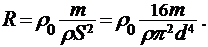
Из справочных таблиц находим
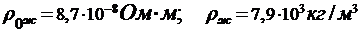 ,
,
тогда
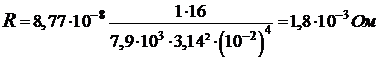 .
.
З.З. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
300. Точечные заряды q1 = 2 мкКл и q2 = -10 мкКл находятся на расстоянии d = 5 см друг от друга. Определить напряжённость поля в точке, удалённой на r1 = 3 см от первого u2 = 4 см от второго заряда. Определить также силу F, действующую в этой точке на точечный заряд q = 1 мкКл.
301. В воздухе на расстоянии 6 см друг от друга находятся два точечных заряда 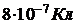 и
и 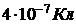 . Найти напряжённость и потенциал поля в точке, отстоящей от положительного заряда на расстоянии 5 см и от отрицательного на 4 см.
. Найти напряжённость и потенциал поля в точке, отстоящей от положительного заряда на расстоянии 5 см и от отрицательного на 4 см.
302. Две бесконечно длинные положительно и равномерно заряженные нити расположены параллельно друг другу на расстоянии 6 см. Геометрическое место точек, где результирующая напряжённость поля равна нулю, расположено в два раза дальше от нити с линейной плотностью заряда 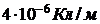 , чем от второй нити, линейную плотность которой требуется определить.
, чем от второй нити, линейную плотность которой требуется определить.
303. Две бесконечно длинные, равномерно заряженные нити с линейной плотностью заряда 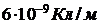 и
и 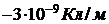 расположены параллельно на расстоянии 12 см друг от друга. Установить геометрическое место точек, где результирующая напряжённость поля равна нулю.
расположены параллельно на расстоянии 12 см друг от друга. Установить геометрическое место точек, где результирующая напряжённость поля равна нулю.
304. Определить напряжённость E поля, создаваемого тонким, длинным стержнем, равномерно заряженным с линейной плотностью 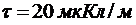 в точке, находящейся на расстоянии A = 2 см от стержня вблизи его середины.
в точке, находящейся на расстоянии A = 2 см от стержня вблизи его середины.
305. На бесконечном тонкостенном цилиндре диаметром d = 20 см равномерно распределён заряд с поверхностной плотностью 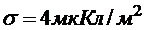 . Определить напряжённость поля в точке, отстоящей от поверхности цилиндра на A = 15 см.
. Определить напряжённость поля в точке, отстоящей от поверхности цилиндра на A = 15 см.
306. Две длинные, прямые, параллельные нити находятся на расстоянии d = 5 см друг от друга. На нитях равномерно распределены заряды с линейными плотностями 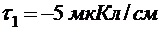 и
и 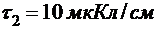 . Определить напряжённость E электрического поля в точке, удаленной от первой нити на расстояние r1 = 3 см, от второй на расстояние r2 = 4 см.
. Определить напряжённость E электрического поля в точке, удаленной от первой нити на расстояние r1 = 3 см, от второй на расстояние r2 = 4 см.
307. Две бесконечные плоскости, заряженные с поверхностными плотностями зарядов 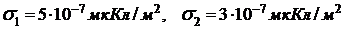 , параллельны друг другу. Чему равна напряжённость поля между плоскостями и вне плоскостей, если:
, параллельны друг другу. Чему равна напряжённость поля между плоскостями и вне плоскостей, если:
1. плоскости заряжены разноимённо (знак заряда на плоскостях разный);
2. плоскости заряжены одноимённо (знак заряда на плоскостях одинаковый)?
308. Два разноимённых заряда 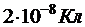 находятся друг от друга на расстоянии 5 см. Третий заряд
находятся друг от друга на расстоянии 5 см. Третий заряд 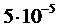 Кл удалён от положительного на расстояние 3 см (рис. 5). Каковы величина и направление действия силы на третий заряд?
Кл удалён от положительного на расстояние 3 см (рис. 5). Каковы величина и направление действия силы на третий заряд?
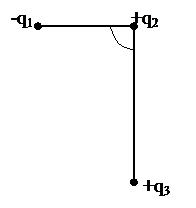

Рис. 5.
309. Точечные заряды q1 = 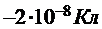 и q2 =
и q2 = 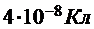 расположены на таком расстоянии, при котором сила взаимодействия между ними равна
расположены на таком расстоянии, при котором сила взаимодействия между ними равна 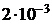 Н . С какой силой действуют эти заряды на третий заряд q3 = 10-7 Кл, находящийся за вторым зарядом на расстоянии 3 см? Все заряды расположены на одной прямой.
Н . С какой силой действуют эти заряды на третий заряд q3 = 10-7 Кл, находящийся за вторым зарядом на расстоянии 3 см? Все заряды расположены на одной прямой.
310. Два положительных точечных заряда q1 и 9 q1 закреплены на расстоянии r = 100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь заряд, чтобы он находился в равновесии, которое было бы устойчиво, если перемещение заряда возможно только по прямой, проходящей через заряды.
311. На расстоянии d = 20 см находятся два точечных заряда q1 = -50 нКл и q2 = 100 нКл. Определить силу F, действующую на заряд q3 = -10 нКл, удалённый от обоих зарядов на одинаковое расстояние, равное d.
312. На тонких нитях длиной 12 см подвешены шарики массой по 1 г. Точка подвеса общая. Им сообщили положительный заряд, и они разошлись на угол 45°. Определить электростатическую силу отталкивания, силу тяготения между ними и величину зарядов шариков.
313. Расстояние r между двумя точечными зарядами q1 = 2 нКл и q2 = 4 нКл равно 60 см. Определить точку, в которую можно переместить третий заряд q3 так, чтобы система зарядов находилась в равновесии. Определить величину и знак заряда. Устойчивое или неустойчивое будет равновесие?
314. Параллельно бесконечной плоскости, заряженной с поверхностной плотностью заряда s = 4 мкКл/м2, расположена бесконечно длинная нить, заряженная линейной плотностью t = 100 нКл/см. Определить силу, действующую на отрезок нити длиной l = 1 см со стороны плоскости.
315. Две одинаковые круглые пластины, площадью S = 400 см2 каждая, расположены параллельно друг другу. Заряд одной пластины q1 = 400 нКл, другой q2 = -200 нКл. Определить силу взаимного притяжения пластин, если расстояние между ними а) r1 = 3 мм, б) r2 = 10 м.
316. С какой силой на единицу площади взаимодействуют две бесконечные параллельные плоскости, заряженные с одинаковой поверхностной плотностью s = 5 мкКл/м2?
317. К бесконечной, равномерно заряженной вертикальной поскости, подвешен на нити одноимённо заряженный шарик массой m = 50 мг и зарядом q = 0,6 нКл. Натяжение нити, на которой висит шарик, F = 0,7 мН. Найти поверхностную плотность заряда s на плоскости.
318. Поверхностная плотность заряда бесконечно протяжённой вертикальной плоскости s = 400 мкКл/м2. К плоскости на нити подвешен заряженный шарик массой 10 г. Определить заряд шарика, если нить образует с плоскостью угол a = 30°.
319. Какое ускорение сообщает электрическое поле Земли, напряжённость которого 130 В/м, заряженной пылинке массой 1 г? Пылинка несёт заряд q = 3,2 10-8 Кл.
320. Определить потенциальную энергию системы двух точечных зарядов q1 = 400 нКл, другой q2 = 20 нКл, находящихся на расстоянии r = 5 см друг от друга.
321. Пылинка массой 20 мкг, несущая на себе заряд q = 40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость v = 10 м/с. Определить скорость v0 пылинки до того, как она влетела в поле.
322. Электрон, обладавший кинетической энергией E = 10 эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов U = 8 В?
323. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрёл скорость v = 105 м/с. Расстояние между пластинами d = 8 мм. Найти: 1) разность потенциалов U между пластинами, 2) поверхностную плотность заряда на пластинах.
324. Пылинка массой m = 5 нг, несущая на себе N = 10 электронов, прошла в вакууме ускоряющую разность потенциалов U = 1 мВ. Какую скорость приобрела пылинка?
325. Ион атома лития Li+ прошёл разность потенциалов U1 = 400 В, ион атома натрия Na+ - разность потенциалов U2 = 300 В. Найти отношение скоростей этих ионов.
326. Два одинаковых воздушных конденсатора, емкостью C = 100 пф каждый, соединены в батарею последовательно. Определить, насколько изменится ёмкость батареи, если пространство между пластинами одного конденсатора заполнить парафином.
327. Две параллельные заряженные плоскости, поверхностные плотности зарядов которых s1 = 2 мкКл/м2 и s2 = -0,8 мкКл/м2 , находятся на расстоянии d = 0,6 см друг от друга. Определить разность потенциалов между плоскостями.
328. Поле образовано бесконечной равномерно заряженной плоскостью с поверхностной плотностью зарядов s = 40 мкКл/м2. Определить разность потенциалов двух точек поля, отстоящих от плоскости на r1 = 15 см и r2 = 20 см.
329. Четыре одинаковые капли ртути, заряженные до потенциала j = 10 В, сливаются в одну. Каков потенциал j1 образовавшейся капли?
330. Электрическое поле образовано бесконечно длиной заряженной нитью, линейная плотность зарядов которой t = 20 нКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r1 = 8 см и r2 = 12 см.
331. Два точечных заряда q1 = 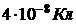 и q2 =
и q2 = 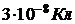 удалены друг от друга на расстояние r = 40 см. Какую работу нужно затратить, чтобы сблизить их до расстояния 15 см? Определить значения потенциалов в точках, где находятся заряды после сближения.
удалены друг от друга на расстояние r = 40 см. Какую работу нужно затратить, чтобы сблизить их до расстояния 15 см? Определить значения потенциалов в точках, где находятся заряды после сближения.
332. Два одинаковых плоских воздушных конденсатора, ёмкостью C = 100 пФ каждый, соединены в батарею параллельно. Определить, насколько изменится ёмкость батареи, если пространство между пластинами одного конденсатора заполнить парафином.
333. Два конденсатора ёмкостью C1 = 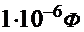 соединены последовательно и присоединены к батареи с ЭДС
соединены последовательно и присоединены к батареи с ЭДС 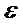 = 80 В. Определить заряд q1 и q2 каждого из конденсаторов и разности потенциалов U1 и U2 между их обкладками.
= 80 В. Определить заряд q1 и q2 каждого из конденсаторов и разности потенциалов U1 и U2 между их обкладками.
334. Плоский конденсатор состоит из двух круглых пластин, радиусом 10 см каждая. Расстояние между пластинами d = 2 мм. Конденсатор присоединён к источнику напряжения U = 80 В. Определить заряд и напряжённость Е поля конденсатора в двух случаях 1) диэлектрик – воздух, 2) диэлектрик – стекло.
335. Два одинаковых плоских воздушных конденсатора соединены последовательно в батарею, которая подключена к источнику тока с ЭДС 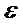 = 12 В. Определить, насколько изменится напряжение на одном из конденсаторов, если другой погрузить в трансформаторное масло.
= 12 В. Определить, насколько изменится напряжение на одном из конденсаторов, если другой погрузить в трансформаторное масло.
336. Плоский конденсатор, с площадью пластин S = 200 см2 каждая, заряжен до разности потенциалов U = 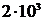 В. Расстояние между пластинами d = 2 см. Диэлектрик – стекло. Определить энергию W поля конденсатора и плотность w энергии поля.
В. Расстояние между пластинами d = 2 см. Диэлектрик – стекло. Определить энергию W поля конденсатора и плотность w энергии поля.
337. На пластинах плоского воздушного конденсатора с площадью пластин 150 см2 находится заряд 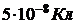 . Какова сила взаимного притяжения между пластинами и объёмная плотность энергии поля конденсатора?
. Какова сила взаимного притяжения между пластинами и объёмная плотность энергии поля конденсатора?
338. Два конденсатора, ёмкостью 5 и 7 мкФ, последовательно присоединены к источнику с разностью потенциалов 200 В. Какова величина зарядов и разность потенциалов батареи, если конденсаторы отсоединить и соединить параллельно?
339. На пластинах плоского воздушного конденсатора равномерно распределён заряд конденсатора 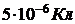 . Площадь обкладок 100 см2, а расстояние между обкладками 3 мм. Заряженный конденсатор отключён от батареи. Какую надо произвести работу при раздвижении пластин до 8 мм?
. Площадь обкладок 100 см2, а расстояние между обкладками 3 мм. Заряженный конденсатор отключён от батареи. Какую надо произвести работу при раздвижении пластин до 8 мм?
340. Пластины плоского воздушного конденсатора площадью 150 см2 раздвигают так, что расстояние между ними увеличивается с 5 до 14 мм. Какую работу необходимо при этом произвести, если напряжение между пластинами конденсатора постоянно и равно 380 В?
341. ЭДС батареи 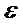 = 80 В, внутреннее сопротивление r0 = 5 Ом. Внешняя цепь потребляет мощность P = 100 Вт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, её сопротивление R.
= 80 В, внутреннее сопротивление r0 = 5 Ом. Внешняя цепь потребляет мощность P = 100 Вт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, её сопротивление R.
342. На концах проводника длиной 3 м поддерживается разность потенциалов 1,5 В. Каково удельное сопротивление проводника если плотность тока j = 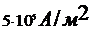 ?
?
343. Катушка из медной проволоки имеет сопротивление R = 10,8 Ом. Масса проволоки m = 3,41 кг. Сколько метров проволоки и какого диаметра d намотано на катушке?
344. Найти сопротивление железного стержня диаметром 1 см, если масса этого стержня 1 кг.
345. Два цилиндрических проводника, один из меди, а другой из алюминия, имеют одинаковую длину и сопротивление. Во сколько раз медный провод тяжелее алюминиевого?
346. Реостат из железной проволоки, миллиамперметр и генератор тока включены последовательно. Сопротивление реостата при нуле градусов Цельсия равно 120 Ом, сопротивление миллиамперметра 20 Ом. Миллиамперметр показывает 22 мА. Что будет показывать миллиамперметр, если реостат нагреется до 50°C?
347. Обмотка из медной проволоки при темпе
