Спонтанное и вынужденное излучения. Лазеры.

Атомы могут нах-ся лишь в квантовых состояниях с дискретными значениями энергии Е1, Е2,… Ради простоты рассмотрим только два из этих состояний (1 и 2). Если атом нах-ся в основном состоянии 1, то под действием внешнего излучения может осуществиться вынужденный переход в возбужденное состояние 2 (рис.1), приводящий к поглощению излучения. Атом, находясь в возбужденном состоянии 2, может через нек-ый промежуток времени спонтанно, без каких-либо внешних воздействий, перейти в состояние с низшей энергией(основное), отдавая избыточную энергию в виде электромагнитного излучения.(испуская фотон с энергией 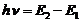). Процесс испускания фотона возбужденным атомом без внешних воздействий наз. Спонтанным излучением. (рис.2) Если на атом, нах-ся в возбужденном

состоянии 2, действует внешнее излучение, то возникает вынужденный переход в основное состояние 1 с излучением фотона.(рис 3) При подобном переходе происходит излучение атомов фотона дополнительно к тому фотону, под действием к-го произошел переход. Возникающее в результате таких переходов излучение – вынужденное. Т.о., в процесс вынужденного излучения вовлечены два фотона: первичный фотон, вызывающий испускание излучения возбужденным атомом, и вторичный фотон, испущенный атомом.

Лазеры – усиление света с помощью вынужденного излучения. Они генерируют в видимой, инфракрасной и ближней ультрафиолетовой областях. Идея качественно нового принципа усиления и генерации электромагнитных волн, примененная в мазерах (генераторы и усилители, работающие в сантиметровом диапазоне радиоволн) и лазерах, принадлежит рос. Ученым Басову и Прохорову. Важнейшими из сущ. типов лазеров явл. твердотельные, газовые, полупроводниковые и жидкостные. Лазер имеет три основных компонента: 1). Активную среду, в к-ой создаются состояния с инверсией населенностей, 2). Систему накачки (устройство для создания инверсии в активной среде), 3). Оптический резонатор (устройство, выделяющее в пространство избирательное направление пучка фотонов и формирующее выходящий световой пучок). Свойства лазерного излучения: 1). Временная и пространственная когерентность. Время когерентности составляет 10-3с, что соответствует длине когерентности порядка 105м. 2). Строгая монохроматичность 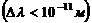3). Большая плотность потока энергии. 4). Очень малое угловое расхождение в пучке. Применяются: для обработки и микросварки твердых металлов, получение и исследование высокотемпературной плазмы, в измерительной технике, в голографии.

46В квантовой статистике системы, состоящие из огромного числа частиц, исследуются с помощью законов квантовой механики, в основе которых ле­жат корпускулярно – волновой дуализм частиц ве­щества и принцип неразли­чимости тождественных частиц. Послед­ний означает, что все одинаковые частицы (например, электроны в металле) являются неразличимыми друг от друга.

В квантовой статистике ставится задача о распределении частиц по ячей­кам фазового пространства (шестимерного пространства коорди­нат и скоро­стей), элемент которого равен 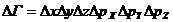, а также задача опре­деления средних значений физических величин, характеризующих мак­роскопическое состояние системы. Состоянию частицы в фазовом простран­стве, с учетом соотношения неопреде­ленностей Гейзенберга, соответствует не точка, а ячейка фазового объема h3, где h – постоянная Планка.

Частицы, число которых равно ΔNi в объеме ΔГi , могут различ­ными спо­собами распределиться между Δgi состояниями с энергией Ei. Тогда число квантовых состояний в объеме ΔГi с энергиями от Ei до Ei + ΔEi равно

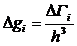. (1)

Среднее значение любой функции определяется с помощью функ­ции рас­пределения, которая позволяет также найти вероятность дан­ного состояния системы.

Ф-ция распред-ия Ф-Д. фазовое пр-во – пр-во 6 измерений, где состояние каждой частицы опредл-ся 6 координатами.

В квантовой механике различают два вида частиц: бозоны – час­тицы с це­лым или нулевым спином (в единицах ), на которые не рас­пространяется принцип Паули и подчиняющиеся распределению Бозе-Эйнштейна (напри­мер, некоторые ядра, фотоны, фононы) и фермионы– частицы с полуцелым спином (электроны, протоны, ней­троны и т.д.). Последние описываются квантовой статистикой Ферми-Дирака и подчиняются принципу Паули, со­гласно которому в каж­дом квантовом состоянии может находиться только одна частица. Функция распределения Бозе-Эйнштейна fБ выражает среднюю “насе­ленность” бозонами состояний с данной энергией или среднее их число в одном состоянии:

,

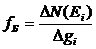где 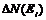- число частиц с энергией в интервале от Ei до Ei + ΔEi;

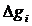- число квантовых состояний в этом интервале энергий.

Распределение бозонов по энергиям получается из канонического распре­деления Гиббса при условии сохранения энергии E в системе и числа частиц N:

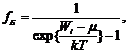(2)

где k – постоянная Больцмана, Т – термодинамическая температура,

μ – химический потенциал, равный работе, совершаемой в изобарно-изотер­мических условиях при увеличении числа частиц в системе на единицу.

m ≤ 0, иначе среднее число бозонов в данном состоянии ста­новится отрица­тельным, что лишено смысла.

Функция распределения Ферми-Дирака определяется аналогично:

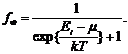(3)

Здесь μ, в отличие от (13.2), может быть положительным.

Функции распределения в классической (Максвелла-Больцмана) и кванто­вой статистиках, интерпретируемые как среднее число частиц в одном со­стоянии, можно выразить единой формулой:

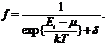(4)

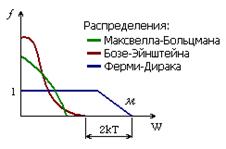
Для распределения Максвелла-Больцмана δ = 0 и μ = 0, для распределения Бозе-Эйнштейна δ = -1 и для распределения Ферми-Дирака δ = +1. Все три распреде­ления показаны на рис. 1.

Система частиц называется вырожденной, если ее свойства описываются квантовыми закономерностями. Вырождение становится существенным для бозе- или ферми-газов при низких температурах и больших плотностях.

Рис. 1

Параметром вырождения А называется вели­чина 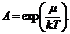При A<<1 (малое вырождение) в (13.4) можно пренеб­речь вели­чиной δ и квантовые функции распределения переходят в классиче­скую. Параметр А определяется из условия сохранения общего числа частиц:

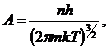(5)

где n – концентрация частиц, m – масса частицы, Т – температура, k –посто­янная Больцмана, h – постоянная Планка.

Примером вырожденного газа являются электроны в металле, которые не подчиняются классической статистике Максвелла-Больцмана.

47Согласно корп-волн. дуализму свойств ве-ва, упругим волнам в кристалле сопоставляют фононы, обладающ. энергией 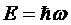.Фонон есть квант энергии звук. волны. Фононы явл. квазичастицами – элемент. возбуждениями, ведущими себя подобно микрочастицам. Квазичаст. существ. только в кристаллах. Свойства импульса фонона: при столк. фононов в крист. их импульс может дискретн. порциями передав. крист. решетке – он при этом сохраняется. Поэтому в случ. фононов говорят о квазиимпульсе.

Класс. теория не смогла объяснить завис. теплоемкости тв. тел от температуры, а квант. статист. решила эту задачу, колеб атомов в крист решетке не явл независимыми.