Прохождение частицы через потенциальный барьер

Рассмотрим 2 случая: классический и квантовый. (Анимации). В квантовомеханическом случае возможен туннельный эффект. Вводится коэффициент прозрачности барьера:

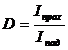. (10)

(10) дает вероятность прохождения волн де Бройля сквозь потенциальный барьер. По аналогии с оптикой вводится и коэффициент отражения R=1-D.

Для прямоугольного барьера

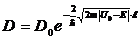. (11)

Для произвольного барьера

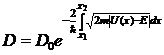. (12)

Туннельный эффект имеет место, когда D не слишком мала, т.е. показатель степени близок к 1. Это возможно при ℓ порядка атомных размеров.

Пример: U-E ≈ 10 eV, me ≈ 10-30 kg, ℓ ≈ 10-10 м , степень ≈ 1 и D ≈ 1/e.

Парадокс туннельного эффекта: Если E‹ U, то Екин ‹ 0. Но туннельный эффект чисто квантовое явление и, кроме того, Е ≠ Ек + Ер из-за соотношения неопределенностей Гейзенберга.

Линейный гармонический осциллятор в квантовой механике. Нулевая энергия.

Линейный гармонический осциллятор- система, совершающая одномерное движение под действием квазиупругой силы. Потенциальная энергия гармонического осциллятора 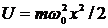, 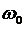- собственная частота, m- масса частицы. Зависимость имеет вид параболы, т.е. «потенциальная яма» в данном случае явл. параболической.

Тогда стационарные состояния квантового осциллятора опред. у-нием Шредингера 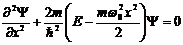, Е- полная энергия.

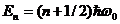- энергия квантового осциллятора принимает дискретные значения, квантуется. Энергия ограничена снизу отличным от нуля, как и для прямоугольной «ямы» с бесконечно высокими «стенками», минимальным значением энергии 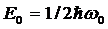. Существование минимальной энергии – она наз. Энергией нулевых колебаний – является типичной для квантовых систем и представляет собой прямое следствие соотношения неопределенностей.

Атом водорода

1885, Формула Бальмера: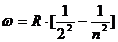

R = 2,07.1016 c-1 .

Обобщенная формула Бальмера: 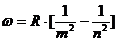, (13)

где n = m + 1,…

Квантовомеханическая задача: .

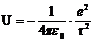Уравнение Шредингера:

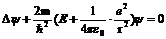. (14)

Решение для стандартных условий:

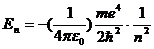. (n = 1,2,3…) (15)

При n = 1 (основное состояние атома): Е1 = - 13,6 эВ.

Собственные функции:

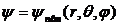. (16)

При данном n: ℓ = 0,1,2,…, n-1

При данном ℓ: m = - ℓ, - ℓ+1, -1, 0, 1,… ℓ-1, ℓ - всего (2 ℓ + 1) значений.

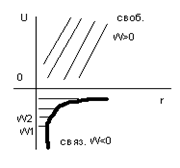Энергия зависит только от n. Следовательно, каждому Еn соответствует несколько собственных функций 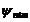с разными ℓ и m. Разные состояния с одинаковой энергией называются вырожденными.

Кратность вырождения

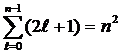. (17)

Возможные состояния электронов:

1s

2s 2p

3s 3p 3d

4s 4p 4d 4f и т.д.

Правило отбора: 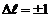. Показать схему переходов.

В дальнейшем было теоретически доказано и подтверждено экспериментами существование у электрона (и других элементарных частиц) собственного момента импульса LS, который не связан с движением электрона в пространстве. Этот собственный момент был назван спином. Спин следует считать внутренним свойством, присущим электрону, подобно тому, как ему присущи заряд или масса.
Модуль собственного момента импульса электрона определяется спиновым квантовым числом S, равным 1/2 :

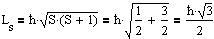, (29)

Проекция спина на ось z может принимать значения

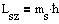(ms=±s= ±1/2 , (30)

где ms - спиновое квантовое число.

44В классической механике частицы одинаковой природы можно различать. В квантовой механике в силу принципа неопределенности понятие траектории частицы утрачивает смысл. Поэтому следить за каждой из одинаковых частиц и тем самым различать их невозможно. Таким образом, в квантовой механике частицы одинаковой природы полностью теряют свою "индивидуальность" - они оказываются неразличимыми.
Принцип неразличимости одинаковых частиц приводит к глубоким физическим следствиям. Оказывается, что частицы с целым или нулевым спином (бозоны) могут находиться в пределах данной системы в одинаковом состоянии в неограниченном количестве. Частицы с полуцелым спином (фермионы) согласно принципу Паули могут находиться в квантовых состояниях только поодиночке.
Принцип Паули (1925 г.)утверждает, что в одном и том же атоме (квантовой системе) не может быть двух электронов (либо других частиц с полуцелым спином), обладающих одинаковой совокупностью квантовых чисел. Иными словами, в одном и том же состоянии не могут находиться одновременно два электрона.
Принцип Паули дает объяснение периодической повторяемости свойств атомов в периодической системе элементов Д.И. Менделеева.