Экспериментальные подтверждения гипотезы и формулы де Бройля

Опыты Девиссона и Джермерра. При заданном угле падения электроны отражаются от пов-ти кристалла под различными углами, причем в одних направлениях наблюдаются максимумы числа отраженных электронов, в других – минимумы, т.е. наблюдалась диф картина. Это явление наблюдается когда длина электронной волны де Бройля имеет порядок межатомного расстояния в кристалле. Длина волны , связанная с электронами, порядка длины волны рентгеновских лучей. Физ смысл волн де Бройля:квадрат амплитуды волны де Бройля в данной точке пр-ва явл-ся мерой вероятности обнаружить частицы в этой точке пр-ва.

38 Соотношение неопределенностей Гейзенберга

квантовая механика раскрывает 2 основных св-ва вещ-ва: квантованность внутриатомных процессов и волновую природу частиц. Скорость света в вакууме явл-ся критерием, определяющим границу применимости классических з-нов, т.к. она явл-ся макс скоростью передачи сигналов.

Т.к. движущая частица обладает корпускулярно- волновым дуализмом, то одновременное точное определение координаты х и импульса р невозможно. Чем точнее определена координата ( 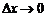) тем менее точно определен импульс ( )

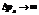Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку величины меньше постоянной Планка, называется принципом неопределенности Гейзенберга.

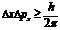
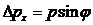
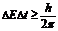
39 Уравнение Шредингера(1926 г.)

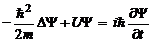. (11)

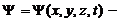комплексная функция координат и времени, характеризует состояние микрочастицы. Это основное уравнение нерелятивистской квантовой механики. Для стационарных состояний оно имеет вид:

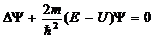. (12)

М. Борн (1926 г) впервые дал интерпретацию пси – функции: квадрат модуля 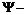функции определяет вероятность dP того, что частица будет обнаружена в пределах объема dV

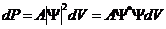(13)

А - коэффициент пропорциональности, для пси-функции выполняется следующее условие нормировки:

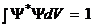(14)

Из смысла функции(волновая) вытекает, что квантовая механика имеет статистический характер. Уравнение Шредингера позволяет найти пси – функцию данного состояния и, следовательно, определить вероятность нахождения частицы в различных точках пространства. Из уравнения (14) и условий, налагаемых на пси – функцию, непосредственно вытекают правила квантования энергии.

Пси – функция должна быть однозначной, непрерывной и конечной, кроме того она должна иметь непрерывную и конечную производную – стандартные условия.

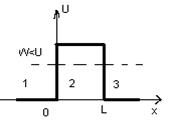
Частица в потенциальной яме

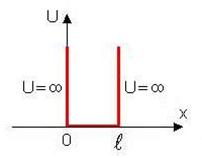Пусть частица движется вдоль оси х в бесконечно глубокой потенциальной яме ширины l. Потенциальная энергия в этом случае равна нулю внутри "ямы" и обращается в бесконечность повсюду вне ее (рис. 1).

Из-за бесконечной высоты потенциальных стенок частица не может попасть за пределы потенциальной ямы, следовательно, вне ямы функция Ψ = 0. Из условия непрерывности на границах ямы:

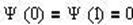. (1)

Рис.1

Используем стационарное уравнение Шредингера:

.

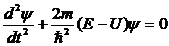В области 0 < x < l уравнение Шредингера имеет вид:

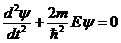. (2)

Обозначим

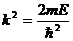. (3)

Тогда уравнение примет вид:

Ψ // + k2 Ψ = 0. (4)

Решение:

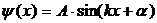. (5)

Используем (1) для определения k и α. Из 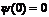получим ,

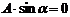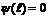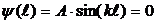откуда α = 0. Из имеем и

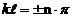, где n = 1,2,3… (6)

n – главное квантовое число.

Подставим (6) в (3) и найдем собственные значения энергии:

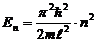. (n = 1,2,3…) (7)

Спектр энергии оказался дискретным.

Оценим расстояние между соседними энергетическими уровнями

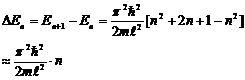.Для молекул (m ~ 10-26 кг) газа, заключенного в сосуд с размерами l ~ 0,1 м, расчет дает, что ΔЕn~10-39 n, Дж = 10-20 n, эВ. Столь густо расположенные энергетиче­ские уровни образуют практически сплошной спектр энергии, так что кван­тование энергии на характере движения молекул сказываться не будет. Но для электрона, заключенного в области атома размера (l ~ 10-10 м), получа­ется совсем иной результат: ΔЕn~102 n, эВ. Здесь заметна дискретность уровней.

Волновая функция имеет вид:

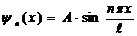. (8)

Используем условие нормировки:

.

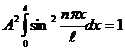На границах функция =0, поэтому интеграл среднему значению функции, умноженному на длину интервала ℓ, т.е.

,

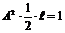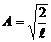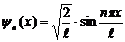откуда и . (9)

Рассмотрим графики.

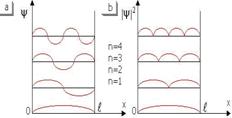
РИС.2

Принцип соответствия Бора

Рассмотрим влияние квантового числа n на характер расположения уровней.

Возьмем отношение 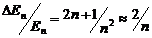. С ростом n отношение уменьшается, т.е. имеет место относительное сближение уровней.

В 1923 году Н. Бор сформулировал принцип соответствия: При больших квантовых числах результаты и выводы квантовой механики должны соответствовать классическим выводам и результатам.