Свободные электроны в металле

Модель свободных электронов объясняет электрические и магнитные свойства твердых тел, в первую очередь металлов. В этой модели свободные электроны (фермионы) могут перемещаться по всему объему металла, не выходя за его пределы, и рассматриваются как идеальный газ. Квантовые системы фермионов, к которым относится электронный газ, описываются функцией распределения Ферми–Дирака

.

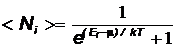Электроны подчиняются принципу Паули, поэтому в каждом состоянии может находиться один свободный электрон, характеризуемый двумя квантовыми числами – главным и спиновым. Энергетические уровни в металле при T = 0K заполняются электронами последовательно с низшего (основное состояние) до наивысшего - уровня Ферми, а выше него уровни свободны. Функция распределения Ферми–Дирака может быть представлена в другом виде:

.

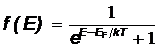Здесь f(E)- вероятность заполнения электронами состояния с энергией Е (f(E)=1, если на уровне находятся два электрона), 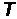- абсолютная температура, 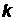- постоянная Больцмана, E_F - энергия Ферми.

При T=0 функция распределения имеет вид (Рис.24):

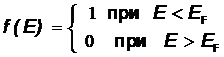
Рис.24 Функция распределения Ферми-Дирака при Т = 0

При Т = 0 распределение свободных электронов в металле по энергиям определяется следующим выражением:

,

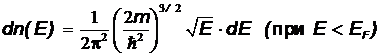где 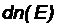–концентрация электронов, энергия которых заключена в интервале значений от E до dE; 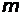и E – масса и энергия электрона; E_F – уровень (энергия) Ферми. Интегрирование этого выражения дает

,

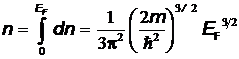откуда энергия Ферми равна

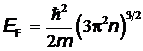
и составляет для металлов несколько электронвольт.

Температура 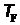(температура вырождения или температура Ферми) определяется равенством 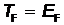. При 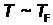энергия теплового движения электронов в металле сравнима c энергией Ферми. 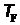определяется равенством:

,

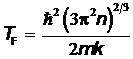где 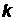–постоянная Больцмана, 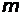–масса электрона, 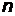–концентрация электронов. При температурах 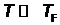электронная подсистема металла должна рассматриваться в рамках квантовой механики. Количественная оценка температуры вырождения дает 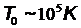, откуда следует, что при всех температурах, пока металл остается твердым, его свободные электроны являются вырожденной системой.

При 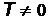и энергии 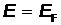функция 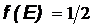. Следовательно, вероятность заполнения состояния на уровне Ферми равна 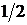(Рис.25).

Рис.25 Функция распределения Ферми-Дирака при Т >0 для свободного электронного газа в металле

На Рис.25 видно, что с ростом температуры происходит размытие «ступеньки» функции распределения Ферми – Дирака без изменения ее площади (общее число электронов остается постоянным). Лишь небольшая часть электронов, находящихся в состояниях вблизи уровня Ферми переходит под действием теплового движения на более высокие уровни. Ширина области размытия имеет величину порядка kT , поэтому в нагревании металла участвует доля электронов, примерно равная 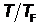. Поэтому теплоемкость электронов составит

Напомним, что в классической теории свободные электроны рассматривались как одноатомные молекулы, имеющие теплоемкость 3/2R. Расчеты показывают, что при комнатной температуре