Спин и магнитный момент электрона
О. Штерн и В. Герлах в своих опытах обнаружили, что узкий пучок атомов водорода, находящихся в s-состоянии в неоднородном магнитном поле расщепляется на два пучка. В s-состоянии (момент импульса и магнитный момент электрона равны нулю), поэтому магнитное поле не должно оказывать влияние на движение атомов водорода, т.е. расщепления быть не должно. Для объяснения этого и других явлений Гаудсмит и Уленбек предположили, что электрон обладает собственным моментом импульса (вращается вокруг своей оси), который был назван спином (от английского слова spin – верчение, кручение). Для механического  и магнитного
и магнитного  собственных моментов электрона должно выполняться гиромагнитное отношение, однако, экспериментально было установлено, что это отношение в два раза больше
собственных моментов электрона должно выполняться гиромагнитное отношение, однако, экспериментально было установлено, что это отношение в два раза больше  , поэтому представление об электроне как о вращающемся шарике оказывается несостоятельным. Дальнейшие эксперименты показали, что спин - существенно квантовая величина, не имеющая классического аналога и являющаяся, подобно массе и заряду, внутренней характеристикой электрона и других элементарных частиц. Оказалось, что существование спина и его свойства вытекают из полученного П.Дираком релятивистского уравнения квантовой механики (аналога нерелятивистского уравнения Шредингера).
, поэтому представление об электроне как о вращающемся шарике оказывается несостоятельным. Дальнейшие эксперименты показали, что спин - существенно квантовая величина, не имеющая классического аналога и являющаяся, подобно массе и заряду, внутренней характеристикой электрона и других элементарных частиц. Оказалось, что существование спина и его свойства вытекают из полученного П.Дираком релятивистского уравнения квантовой механики (аналога нерелятивистского уравнения Шредингера).
Величина собственного момента импульса микрочастицы определяется в квантовой механике с помощью спинового квантового числа s, которое часто называют «спином» и которое принимает целые 0,1,2,… или полуцелые  ,
,  и т.д. значения. Спин электрона, протона, нейтрона
и т.д. значения. Спин электрона, протона, нейтрона  , а спин фотона
, а спин фотона  .
.
Как и орбитальный момент, собственный механический момент импульса микрочастицы  определяется модулем
определяется модулем
 .
.
и проекцией  на ось z
на ось z
 ,
,
где  - спиновое магнитное квантовое число, часто называемое проекцией спина. Спиновое квантовое число
- спиновое магнитное квантовое число, часто называемое проекцией спина. Спиновое квантовое число  принимает 2s + 1 значений -s,-s + 1,…,0,1,…,s
принимает 2s + 1 значений -s,-s + 1,…,0,1,…,s
Для электрона  может принимать только два значения
может принимать только два значения  и характеризует возможные значения проекции на ось
и характеризует возможные значения проекции на ось 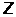 спина (собственного механического момента)
спина (собственного механического момента)  электрона. Таким образом, электрон в атоме водорода характеризуется четырьмя квантовыми числами n, l, m и ms (Таблица 2).
электрона. Таким образом, электрон в атоме водорода характеризуется четырьмя квантовыми числами n, l, m и ms (Таблица 2).
Таблица 2
Собственные значения орбитального и спинового моментов и их проекции на ось 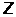 .
.
 |  |
 |  |
 |  |
 |  |
Поскольку гиромагнитное отношение для спина электрона равно не  , то спиновый магнитный момент и его проекция на произвольную ось
, то спиновый магнитный момент и его проекция на произвольную ось 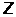 определяются как
определяются как
 ,
,  , при
, при 
 и
и  .
.
Таким образом, проекция спинового магнитного момента электрона на ось z равна одному магнетону Бора. Различные состояния электрона в атоме принято обозначать малыми буквами латинского алфавита в зависимости от значения орбитального квантового числа  . Они приведены в таблице 3.
. Они приведены в таблице 3.
Таблица 3
Значение орбитального квантового числа 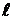 | |||||
| Символ соответствующего состояния электронов | s | p | d | f | g |
И далее символы идут по алфавиту.
Принято говорить об s - состояниях (или s - электронах), 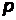 - состояниях (или
- состояниях (или 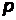 - электронах) и т.д. Значение главного квантового числа
- электронах) и т.д. Значение главного квантового числа 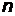 указывают перед символом состояния с данным
указывают перед символом состояния с данным  . Например, электрон, имеющий главное квантовое число
. Например, электрон, имеющий главное квантовое число  и
и  , обозначают символом
, обозначают символом  и т.д.
и т.д.
Все волновые функции, соответствующие  - состояниям электрона в атоме водорода, сферически симметричны. Это означает, что вероятность обнаружить электрон на некотором расстоянии
- состояниям электрона в атоме водорода, сферически симметричны. Это означает, что вероятность обнаружить электрон на некотором расстоянии  вблизи ядра зависит только от этого расстояния. В
вблизи ядра зависит только от этого расстояния. В  -состоянии (
-состоянии (  ) волновая функция не зависит от углов q и j.
) волновая функция не зависит от углов q и j.
Нормированные собственные Y-функции, отвечающие  –состоянию (основному) и
–состоянию (основному) и  –состоянию:
–состоянию:
 ,
,
 ,
,
где  – первой боровский радиус
– первой боровский радиус
Вероятность  того, что электрон находится в области, ограниченной эле
того, что электрон находится в области, ограниченной эле
ментом объема  , взятого в окрестности точки с координатами
, взятого в окрестности точки с координатами  :
:
 ,
,
где  – элемент объема в сферических координатах.
– элемент объема в сферических координатах.
Вероятность  найти электрон в атоме водорода, находящемся в
найти электрон в атоме водорода, находящемся в  –состоянии, в интервале
–состоянии, в интервале  одинакова по всем направлениям и определяется формулой
одинакова по всем направлениям и определяется формулой  , где
, где  –собственная нормированная радиальная волновая функция
–собственная нормированная радиальная волновая функция  –состояния (
–состояния (  ),
),  –элемент объема в виде сферического слоя радиусом
–элемент объема в виде сферического слоя радиусом  и толщиной
и толщиной  .
.
Плотность вероятности обнаружения электрона в сферическом слое между  и
и  можно представить в виде
можно представить в виде  . Величину
. Величину  называют радиальной плотностью вероятности – произведение
называют радиальной плотностью вероятности – произведение  дает вероятность того, что электрон будет обнаружен на расстоянии от ядра между
дает вероятность того, что электрон будет обнаружен на расстоянии от ядра между  и
и  .
.
 .
.
 .
.
Графики радиальной плотности вероятности  , а также
, а также  пред-
пред-
ставлены на Рис.20.

Рис.20 Зависимость радиальной плотности вероятности от расстояния до ядра
14. Принцип Паули.
В атоме не могут находиться два электрона с четырьмя одинаковыми квантовыми числами  . Принцип Паули является следствием принципа неразличимости тождественных частиц. В состояниях с данным значением
. Принцип Паули является следствием принципа неразличимости тождественных частиц. В состояниях с данным значением 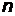 в атоме могут находиться не более
в атоме могут находиться не более  электронов (таблица 4):
электронов (таблица 4):
Таблица 4
 | 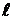 =0 =0 |  |  |
 | 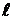 =0 =0 |  |  |
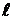 =1 =1 |  |  | |
 | 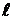 =0 =0 |  |  |
 =1 =1 |  |  | |
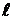 =2 =2 |  |  |
По мере увеличения порядкового номера  атома в соответствии с принципом Паули происходит последовательное строго определенное заполнение электронных уровней атома. Число электронов, находящихся в квантовом состоянии, описываемом набором четырех квантовых чисел
атома в соответствии с принципом Паули происходит последовательное строго определенное заполнение электронных уровней атома. Число электронов, находящихся в квантовом состоянии, описываемом набором четырех квантовых чисел  :
:  .
.
Максимальное число электронов  , находящихся в состояниях, определяеых набором трех квантовых чисел
, находящихся в состояниях, определяеых набором трех квантовых чисел  :
:  = 2
= 2
Максимальное число электронов  , находящихся в состояниях, опре-
, находящихся в состояниях, опре-
деляемых двумя квантовыми числами  :
:  =2(2
=2(2 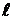 +1).
+1).
Максимальное число электронов  , находящееся в состояниях, опреде-
, находящееся в состояниях, опреде-
ляемых данным главным квантовым числом n (таблица 5):
 .
.
Таблица 5
Значение орбитального квантового числа 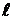 | |||||
| Символ соответствующего состояния электронов | s | p | d | f | g |
| Максимальное число электронов |
Электроны атома с одинаковыми квантовыми числами 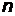 , образуют оболочку.
, образуют оболочку.
В соответствии со значением 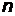 оболочки обозначают большими буквами латинского алфавита следующим образом (таблица 6):
оболочки обозначают большими буквами латинского алфавита следующим образом (таблица 6):
Таблица 6
Значение 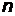 | ||||||
| Оболочка |  |  |  |  |  |  |
Оболочки подразделяют на подооболочки, отличающиеся квантовым числом  .
.
Подоболочки обозначают в виде  , где цифра означает
, где цифра означает
квантовое число 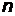 , т.е. принадлежность к соответствующей оболочке:
, т.е. принадлежность к соответствующей оболочке:

Возможные состояния электронов в атоме и их распределение по оболочкам и подоболочкам показаны в таблице 7, в которой вместо обозначений  и
и  использованы для наглядности знаки и ¯.
использованы для наглядности знаки и ¯.
Таблица 7
| Оболочка | K | L | M | |||||||||||
Подоболочка (  ) ) | 1s | 2s | 2p | 3s | 3p | 3d | ||||||||
| m | +1 | -1 | +1 | -1 | +2 | +1 | -1 | -2 | ||||||
| ms | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ |
| Число электронов |
Распределение электронов по оболочкам и подоболочкам называют электронной конфигурацией. Она записывается следующим образом: число слева обозначает главное квантовое число или номер оболочки, латинская буква – значение орбитального квантового числа или подоболочки, а верхний индекс справа – число электронов в подоболочке (например, обозначению  отвечает электрон с
отвечает электрон с  и
и  ;
;  означает, что таких электронов в атоме 2, и т.д.). Символическое обозначение электронной конфигурации одного из атомов
означает, что таких электронов в атоме 2, и т.д.). Символическое обозначение электронной конфигурации одного из атомов  означает, что в нем имеются два
означает, что в нем имеются два  –электрона, два
–электрона, два  – , шесть
– , шесть  –электронов и один
–электронов и один  –электрон.
–электрон.
Принцип Паули лежит в основе построения периодической системы элементов Менделеева. Поскольку любая система, в том числе атом, стремится занять состояние с наименьшенй энергией, то электроны последовательно заполняют K, L и M оболочки, начиная с Z = 1 (водород) до Z = 18 (аргон). Девятнадцатый электрон (в калии) должен был бы занять место в 3d подоболочке M оболочки, однако, в действительности, он занимает место в 4s подоболочке N оболочки. Это объясняется тем, что состояние n = 4,  имеет меньшую энергию, чем состояние n = 3,
имеет меньшую энергию, чем состояние n = 3,  . Подобные нарушения встречаются и при дальнейшем заполнении электронами энергетических уровней элементов периодической системы.
. Подобные нарушения встречаются и при дальнейшем заполнении электронами энергетических уровней элементов периодической системы.
