Решение уравнения Шредингера для движения частицы в одномерной бесконечной потенциальной яме.

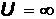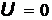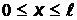Функция при x < 0 и ; при (Рис.16).

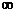
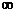
Рис.16 Бесконечно глубокая одномерная прямоугольная потенциальная яма

Уравнение Шредингера в этом случае имеет вид:

,

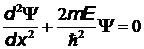где 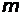- масса частицы, E – ее энергия. Введем обозначение 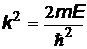, тогда

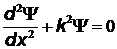
Движение при x < 0 и движение невозможно ( 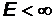), поэтому в этих областях 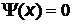. В силу непрерывности волновой функции 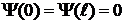. Решение уравнения имеет вид

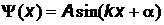
и должно удовлетворять граничному условию 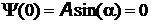, откуда a=0. Второе граничное условие

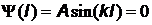
выполняется при 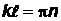, откуда 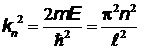. Это означает, что уравнение Шредингера имеет решения только для значений энергии, удовлетворяющих условию

( ).

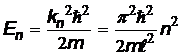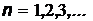Соответствующие E_n собственные волновые функции частицы имеют вид:

,

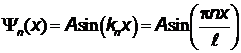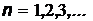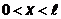, . Для определения A необходимо воспользоваться условием нормировки,

,

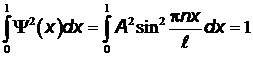откуда окончательно

.

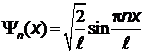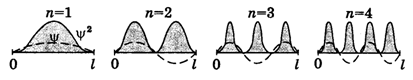Графики волновых функций нескольких состояний показаны на Рис.17 пунктирными линиями, а функции плотности вероятности – сплошными.

Рис.17 Графики волновых функций и функций плотности вероятности

Плотность вероятности нахождения частицы на единице длины в том или ином месте внутри одномерной бесконечной прямоугольной потенциальной ямы:

,

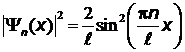а вероятность обнаружения микрочастицы между координатами х₁ и х₂ внутри потенциальной ямы:

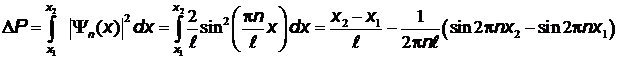
Примеры решения задач.Во всехпримерах рассматривается движение частицы (электрона) в бесконечно глубокой одномерной прямоугольной потенциальной яме шириной 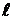, сокращенно – в потенциальной яме.

Задача 1.Электрон находится в потенциальной яме шириной 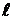. Вычислите вероятность того, что находясь в возбужденном состоянии (n=2), он будет обнаружен в средней трети ямы.

Решение.Вероятность 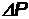обнаружить частицу в интервале 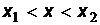определяется равенством

,

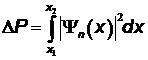где 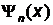- нормированная собственная волновая функция, отвечающая данному состоянию. Возбужденному состоянию 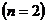отвечает собственная функция

.

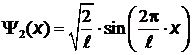Тогда вероятность равна

.

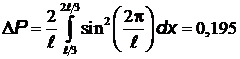Задача 2. Электрон находится в потенциальной яме шириной 1,4 нм. Определите энергию, излучаемую при переходе электрона с третьего энергетического уровня на второй.

Решение.Энергия 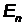электрона массой 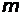, находящегося на п – ом энергети

ческом уровне в потенциальной яме шириной 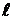, определяется по формуле:

.

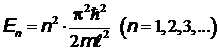Энергия, излучаемая при переходе электрона с 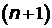- го уровня на 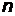- й, равна

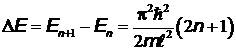= 1,54×10^–19 Дж = 1 эВ.

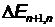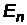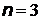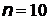Задача 3. Частица находится в потенциальной яме. Найдите отношение разности соседних энергетических уровней к энергии частицы в трех случаях: 1) ; 2) ; 3) .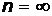

Решение.Собственное значение энергии частицы 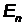, находящейся на 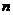-ом энергетическом уровне в бесконечно глубокой одномерной прямоугольной потенциальной яме, определяется выражением: 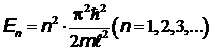. Здесь 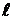- ширина потенциальной яме.

.

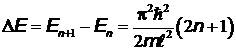Отношение разности соседних энергетических уровней к энергии частицы имеет вид:

,

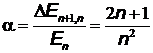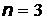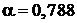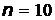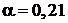при : , при : при : .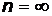

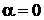Задача 4.Частица в потенциальном яме шириной 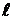находится в возбужденном 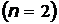состоянии. Определите, в каких точках интервала 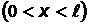плотность

вероятности 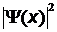нахождения частицы максимальная и минимальна.

Решение.Нормированная собственная волновая функция, описывающая состояние электрона в потенциальном ящике, имеет вид: .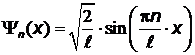

Возбужденному состоянию 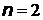отвечает плотность вероятности:

.

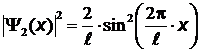Функция максимальна при 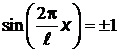, отсюда .

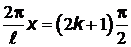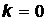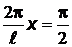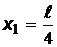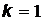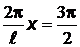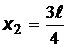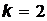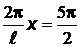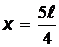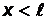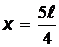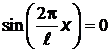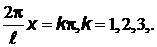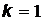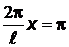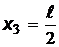При : ; . При : ; . При : ; . , поэтому не удовлетворяет условию задачи. Функция минимальна при ; При : ; . При 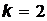: 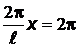; 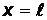. По условию 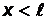, поэтому 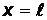не является решением. Тогда плотность вероятности максимальна пр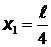и и 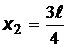, а минимальна при .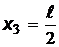