Линия влияния изгибающих моментов и поперечных сил в сечении 1

Сечение 1 принадлежит консольной балке AB. Линии влияния изгибающего момента и поперечной силы строятся для этой балки, как для правой консоли двух опорной балки (см. линии влияния M₆ и Q₆на рис.10). Достраиваем линии влияния M₁и Q₁на вышерасположенную балкуBC. Соединяем ординаты линий влияния M₁и Q₁в сечении B с нулем в шарнире C.

Линия влияния изгибающих моментов и поперечных сил в сечении 2

Сечение 2 принадлежит балке CDEK – это двух опорная балка со свисающими консолями. Линию влияния M₂строим в соответствии с рис.10(линия влияния M₄). Отложим двойку (a=2) под опорой D, соединим с нулем на опоре E и продлим влево на величину консольного вылета, получим правую ветвь линии влияния M₂. Отложим двойку (b=2) под опорой E, соединим с нулем на опоре D и продлим вправо на величину консольного вылета, получим левую ветвь линии влияния M₂. Ординаты линии влияния в сечениях C и K балки CDEK определим из отношений сторон подобных треугольников. Достраиваем линию влияния на вышерасположенные балкиBC и KLT. Соединяем ординату линии влияния в сечении C с нулем в шарнире B , а ординату линии влияния в сечении K с нулем на опоре L и продлеваем вправо на величину консольного вылета LT. Ординату линии влияния в сечении T определим из отношений сторон подобных треугольников.

Линию влияния Q₂строим в соответствии с рис.10(линии влияния Q₄). Отложим единицу под опорой D, соединим с нулем на опоре E и продлим влево на величину консольного вылета, получим правую ветвь линии влияния Q₂. Отложим единицу под опорой E, соединим с нулем на опоре D и продлим вправо на величину консольного вылета, получим левую ветвь линии влияния Q₂. Ординаты линии влияния в сечениях C и K балки CDEK определим из отношений сторон подобных треугольников. Достраиваем линию влияния на вышерасположенные балкиBC и KLT. Соединяем ординату линии влияния в сечении C с нулем в шарнире B , а ординату линии влияния в сечении K с нулем на опоре L и продлеваем вправо на величину консольного вылета LT. Ординату линии влияния в сечении T определим из отношений сторон подобных треугольников.

Определение внутренних силовых факторов и реакций опор

По линиям влияния

Чтобы определить значение реакции опоры, изгибающего момента или поперечной силы в каком-либо сечении балки, необходимо построить соответствующую линию влияния реакции или внутреннего силового фактора для этого сечения.

Значение реакции опоры, изгибающего момента или поперечной силы в заданном сечении по соответствующей линии влияния определяется по формуле: S = 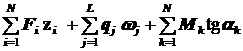, где

S – искомая величина (опорная реакция, изгибающий момент или поперечная сила в заданном сечении);

F_i – внешняя сосредоточенная сила, положительна, если направлена вниз;

q_j – интенсивность распределенной нагрузки, положительна, если направлена вниз;

M_k – внешний сосредоточенный момент, положительный, если направлен по ходу часовой стрелки;

z_i – ордината линии влияния в сечении балки под соответствующей силой, берется со своим знаком;

ω_j – площадь участка линии влияния, расположенного в пределах распределенной нагрузки, знак которой определяется знаком соответствующей линии влияния;

tgα_k – тангенс угла наклона линии влияния под сосредоточенным моментом,положительныйдля восходящей ветви линии влияния.

Согласно приведенной формуле, при вычислении значения реакции опоры, изгибающего момента или поперечной силы в заданном сечении необходимо просуммировать произведения всех действующих на балку сил, моментов и распределенных нагрузок, на соответствующие параметры линии влияния.

Задача 1

Для заданной схемы балки (рис.12) требуется:

1. Выполнить кинематический анализ системы.

2. Построить поэтажную схему.

3. Построить эпюры изгибающих моментов(M) и поперечных сил (Q).

4. Построить линии влияния поперечной силы (Q) и изгибающего момента(M) для сечений 1 и опоре D.

5.Определить по линиям влияния значения поперечной силы (Q), изгибающего момента(M) для заданного сечения и опорной реакции.

Решение

Кинематический анализ

В заданной схеме балки (рис. 12а): к = 3 (число замкнутых контуров),

ш = 9 (число одиночных шарниров). Степень статической определимости (неопределимости) определяется по формуле S=3к-ш=3·3 – 9=0,

следовательно, балка статически определимая.

Рис.12.Многопролетная балка и её поэтажная схема

Построение поэтажной схемы

Основной или главной является балка АВC, т. к. имеет три кинематические связи. На балке АВC надстраивается подвесная балка CDE, на которой, в свою очередь, - подвесная балка EK(рис. 12б).