Линии влияния изгибающих моментов и поперечных сил

Сечение k располагается внутри пролета двух опорной балки со свисающими консолями.

Для построения линии влияния изгибающего момента в сечении k, расположенном на расстоянии а от левой опоры, надо получить выражение изгибающего момента в зависимости от расположения груза справа или слева от сечения k (рис.9а и рис.9б).

При движении груза справа от сечения k: а ≤ х ≤ l+c (рис. 9а).

Выражение изгибающего момента слева от сечения с учетом правила знаков

M_k= R_А· а

Из уравнения видно, что линия влияния M_k (правая ветвь от сечения k) строится как линия влияния реакции R_А с умножением всех ординат на а.

При движении груза слева от сечения k:– d ≤ х ≤ а (рис. 9б).

Выражение изгибающего момента справа от сечения с учетом правила знаков

M_k= R_B · b

Левая ветвь от сечения k линии влияния M_k строится как линия влияния реакции R_B с умножением всех ординат на b.

При построении линии влияния M_k отложим на левой опоре A величину а, соединим с нулем на опоре B и продлим вправо на величину консольного вылета. Действительная часть этой линии влияния справа от сечения k там, где движется груз. Затем отложим на правой опоре B величину b, соединим с нулем на опоре A и продлим влево на величину консольного вылета. Действительная часть этой линии влияния слева от сечения k там, где движется груз (рис. 9в).

Левая и правая ветви линии влияния изгибающего момента пересекаются под сечением k. Ордината под сечением будет равна ab/l (рис. 9в). Ординаты линий влияния на концах балки определим из подобия соответствующих треугольников.

Рис. 9. Линии влияния изгибающих моментов и поперечных сил

Для построения линии влияния поперечной силы в сечении k, расположенном на расстоянии а от левой опоры, надо получить выражение поперечной силы в зависимости от расположения груза справа или слева от сечения k (рис.9а и рис.9б).

При движении груза справа от сечения k: а ≤ х ≤ l+c (рис. 9а). Выражение поперечной силы слева от сечения с учетом правила знаков

Q_k= R_А,

т.е. правая ветвь от сечения k линии влияния Q_k строится такая же, как линия влияния реакции R_А.

При движении груза слева от сечения k:– d ≤ х ≤ а (рис. 9б). Выражение поперечной силы справа от сечения с учетом правила знаков

Q_k = – R_B,

т.е. левая ветвь от сечения k линии влияния Q_k строится такая же, как линия влияния реакции R_B , ординаты которой берутся с отрицательным знаком.

При построении линии влияния Q_k отложим на левой опоре A величину, равную единице, соединим с нулем на опоре B и продлим вправо на величину консольного вылета. Действительная часть этой линии влияния справа от сечения k там, где движется груз. Затем отложим на правой опоре B величину, равную единице, соединим с нулем на опоре A и продлим влево на величину консольного вылета. Действительная часть этой линии влияния слева от сечения k там, где движется груз (рис. 9г).

Линия влияния поперечной силы в сечении k имеет скачек на величину, pавнyю единице (рис. 9г).

Сечение k располагается в консольной части.

Для построения линий влияния изгибающего момента и поперечной силы в сечении k, расположенном на расстоянии f от правого конца защемленной балки, рассмотрим два положения груза справа или слева от сечения k (рис.9д).

При движении груза справа от сечения k:0 ≤ х ≤ f

M_k = 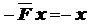; M_k(0) = 0; M_k(f) = – f.

Q_k= .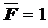

Строим правые ветви линий влияния M_k и Q_k (рис.9е,ж).

При движении груза слева от сечения k (нарис.9д онпоказан пунктирной линией) :0 ≤ х ≤ c – f

Рассматривая правую от сечения k часть балки, получаем M_k =0; Q_k= 0.

Заметим, что для правой консоли двух опорной балки линии влияния изгибающего момента и поперечной силы строятся таким же образом.

Для построения линий влияния изгибающего момента и поперечной силы в сечении k, расположенном на расстоянии e от левого конца защемленной балки, рассмотрим два положения груза справа или слева от сечения k (рис.9з).

При движении груза слева от сечения k: e ≥ х ≥ 0

M_k = 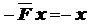; M_k(0) = 0; M_k(f) = – е.

Q_k= – .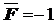

Строим левые ветви линий влияния M_k и Q_k(рис.9и, к).

При движении груза справа от сечения k (нарис.9з онпоказан пунктирной линией) : d – e ≥ х ≥ 0

Рассматривая левую от сечения k часть балки, получаем M_k =0; Q_k= 0.

Заметим, что для левой консоли двух опорной балки линии влияния изгибающего момента и поперечной силы строятся таким же образом.

На рис.10 показаны линии влияния изгибающих моментов и поперечных сил для различных сечений двух опорной балки с консолями, которые широко используются для построения линий влияния в многопролетной балке. Сечения 2 и 3 расположены слева и справа от опоры A, сечения 5 и 6 расположены слева и справа от опоры B. Значения ординат линий влияния не проставленные на этом рисунке легко вычисляются из подобия соответствующих треугольников.

Рис.10. Линии влияния изгибающих моментов и поперечных сил