Вопрос. Спин электрона. Спиновое квантовое число. Распределение электронов в атоме по состояниям. Принцип Паули. Полный спектр атома водорода. Периодическая система элементов Д. И. Менделеева.
Спин (от англ. spin, буквально — вращение, вращать(-ся)) — собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы.
Спин измеряется в единицах ħ[1] (приведённой постоянной Планка, или постоянной Дирака) и равен ħJ, где J — характерное для каждого сорта частиц целое (в том числе нулевое) или полуцелое положительное число — так называемое спиновое квантовое число, которое обычно называют просто спином (одно из квантовых чисел).
В связи с этим говорят о целом или полуцелом спине частицы.
Существование спина в системе тождественных взаимодействующих частиц является причиной нового квантовомеханического явления, не имеющего аналогии в классической механике: обменного взаимодействия.
Вектор спина является единственной величиной, характеризующей ориентацию частицы в квантовой механике[2]. Из этого положения следует, что: при нулевом спине у частицы не может существовать никаких векторных и тензорных характеристик; векторные свойства частиц могут описываться только аксиальными векторами; частицы могут иметь магнитные дипольные моменты и не могут иметь электрических дипольных моментов; частицы могут иметь электрический квадрупольный момент и не могут иметь магнитный квадрупольный момент; отличный от нуля квадрупольный момент возможен лишь у частиц при спине, не меньшем единицы[3].
Спиновый момент электрона или другой элементарной частицы, однозначно отделённый от орбитального момента, никогда не может быть определён посредством опытов, к которым применимо классическое понятие траектории частицы[4].
Число компонент волновой функции, описывающей элементарную частицу в квантовой механике, растёт с ростом спина элементарной частицы. Элементарные частицы со спином {\displaystyle 0} описываются однокомпонентной волновой функцией (скаляр), со спином {\displaystyle {\frac {1}{2}}} описываются двухкомпонентной волновой функцией (спинор), со спином {\displaystyle 1} описываются четырёхкомпонентной волновой функцией (вектор), со спином {\displaystyle 2} описываются шестикомпонентной волновой функцией (тензор)[5].
Если тождественные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Отсюда следует, что два одинаковых фермиона, входящих в одну систему, не могут находиться в одинаковых состояниях, т.к. для фермионов волновая функция должна быть антисимметричной. Обобщая опытные данные, В. Паули сформировал принциписключения, согласно которому системы фермионов встречаются в природе только в состояниях, описываемых антисимметричными волновыми функциями (квантово-механическая формулировка принципа Паули).
| Паули Вольфганг (1900–1958) – физик-теоретик. Работы относятся ко многим разделам современной теоретической физики, в развитии которых он принимал непосредственное участие, в частности квантовой механике, квантовой электродинамике, теории относительности, квантовой теории поля, ядерной физике, физике элементарных частиц. |
Из этого положения вытекает более простая формулировка принципа Паули, которая и была введена им в квантовую теорию (1925 г.) еще до построения квантовой механики: в системе одинаковых фермионовлюбые два из них не могут одновременно находиться в одном и том же состоянии. Отметим, что число одинаковых бозонов, находящихся в одном и том же состоянии, не лимитируется.
Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел:
· главного n ;
· орбитального l , обычно эти состояния обозначают 1s, 2d, 3f;
· магнитного ( );
· магнитного спинового ( ).
Распределение электронов в атоме происходит по принципу Паули, который может быть сформулирован для атома в простейшем виде: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел: n, l, , :
Z (n, l, , ) = 0 или 1,
где Z (n, l, , ) - число электронов, находящихся в квантовом состоянии, описываемых набором четырех квантовых чисел: n, l, , . Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме различаются значениями, по крайней мере, одного квантового числа.
Максимальное число электронов, находящихся в состояниях, описываемых набором трех квантовых чисел n, l и m, и отличающихся только ориентацией спинов электронов равно:
| , | (8.2.1) |
ибо спиновое квантовое число может принимать лишь два значения 1/2 и –1/2.
Максимальное число электронов, находящихся в состояниях, определяемых двумя квантовыми числами n и l:
| . | (8.2.2) |
При этом вектор орбитального момента импульса электрона может принимать в пространстве (2l + 1) различных ориентаций (рис. 8.1).
Рис. 8.1
Максимальное число электронов, находящихся в состояниях, определяемых значением главного квантового числа n, равно:
| . | (8.2.3) |
Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называется электронной оболочкой или слоем.
В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному l.
Область пространства, в которой высока вероятность обнаружить электрон, называют подоболочкой или орбиталью. Вид основных типов орбиталей показан на рис. 8.1.
Поскольку орбитальное квантовое число принимает значения от 0 до , число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2l + 1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам приведено в табл. 1.
Таблица 1
| Главное квантовое число n | |||||||||||||||
| Символ оболочки | K | L | M | N | O | ||||||||||
| Максимальное число электроновв оболочке | |||||||||||||||
| Орбитальное квантовое число l | |||||||||||||||
| Символ подоболочки | 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | 4d | 4f | 5s | 5p | 5d | 5f | 5g |
| Максимальное число электронов в подоболочке |
Спектральные серии водорода
Материал из Википедии — свободной энциклопедии
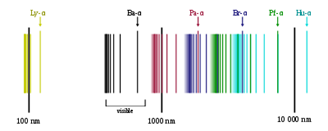
Спектральные линии атома водорода
Спектральные серии водорода — набор спектральных серий, составляющих спектр атома водорода. Поскольку водород — наиболее простой атом, его спектральные серии наиболее хорошо изучены. Они хорошо подчиняются формуле Ридберга:
{\displaystyle {\frac {1}{\lambda }}=R\left({\frac {1}{{n'}^{2}}}-{\frac {1}{n^{2}}}\right)},
где R = 109 677 см−1 — постоянная Ридберга для водорода, n′ — основной уровень серии.
Спектральные линии, возникающие при переходах на основной энергетический уровень, называются резонансными, все остальные — субординатными.
