Вопрос. Квантовая теория фотоэффекта. Уравнение Эйнштейна для внешнего фотоэффекта. Применение фотоэффекта.
В 1905 г. Эйнштейн, опираясь на работы М. Планка по излучению (гл. 11), предложил совершенно новую теорию фотоэффекта. По Эйнштейну, световой поток представляет собой поток «атомов света», названных Эйнштейном фотонами; каждый фотон обладает энергией
E=hv (10.4)
и импульсом
p=E/c
При этом отдельный фотон поглощается отдельным электроном, и электрон приобретает возможность покинуть металл, если его энергия превышает «работу выхода» из металла, характеризуемую разностью потенциалов UK. Применяя закон сохранения
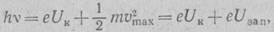 (10.5)
(10.5)
Где 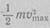 — максимальная кинетическая энергия вылетевшего электрона. За счет взаимодействия с окружающими частицами электрон может вылететь с меньшей энергией, поэтому кривая (см. рис. 10.2) имеет пологий спад.
— максимальная кинетическая энергия вылетевшего электрона. За счет взаимодействия с окружающими частицами электрон может вылететь с меньшей энергией, поэтому кривая (см. рис. 10.2) имеет пологий спад.
Из уравнения (10.5) следует, что существует минимальная частота света,, необходимая для фотоэффекта:
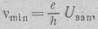
т. е. фотоэффект имеет «красную, границу» (этот термин подчеркивает невозможность возбуждения эффекта при частоте, меньшей νmin). Запирающее напряжение не должно зависеть от интенсивности света; наконец, выполняется уравнение (10.2), упомянутое выше.
Закон Столетова (10.1) означает, что число освободившихся электронов пропорционально числу падающих фотонов, имеющих определенную вероятность поглотиться в данном веществе; Коэффициент пропорциональности меньше единицы, так как не каждый электрон, поглотивший свет, обязательно покинет металл; он может до вылета отдать избыток энергии соседним частицам. Таким образом, фотоэффект получает полное объяснение, но с совершенно новой точки зрения.
Нужно отметить, что Эйнштейн не пользовался законом сохранения импульса. Вероятно, это связано с. неясностью механизма ' взаимодействия электрона с металлом до вылета из последнего. Но следует указать, что импульс фотона (ν≈5 x 10u Гц) равен:
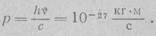
Импульс вылетевшего электрона (при задерживающем потенциале U=1 В) достигает значения:
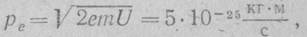
что на два-три порядка превышает импульс фотона.
Поэтому явления, доказывающие приложимость обоих законов сохранения к процессу взаимодействия двух микрочастиц, в теоретическом отношении очень важны (см. эффект Комптона, § 10.5).
Так как вероятность последовательного поглощения двух фотонов. одним и тем же электроном весьма мала, то в первом приближении с таким явлением можно не считаться.
Фототоки при внешнем фотоэффекте невелики. Для их увеличения можно использовать вторичную эмиссию электронов, ускоряя фотоэлектроны в электрическом поле между электродами, причем аноды должны быть сделаны из вещества, дающего значительную вторичную эмиссию электронов. При достаточной энергии первичных электронов число вторичных электронов может превышать число первичных. При повторном осуществлении этой операции на выходе из прибора (фотоумножителя) получается ток, усиленный в тысячи раз; обычные фотоэлементы с внешним фотоэффектом дают ток порядка 10-5 A/лм, а фотоумножитель — до 1 A/лм. При этом безынерционность процесса сохраняется (§ 15.4).
Другой способ увеличения фототока — помещение катода фотоэлемента в газовую среду, где возможно получение ударной ионизации и связанное с этим увеличение тока в десятки раз. Однако п этом случае утрачивается безынерционность, так что газополныефотоэлементы применяются только при медленно меняющихся световых потоках.
В заключение отметим, что детали фотоэффекта более сложны — часто наблюдаются некоторые осложняющие явления.
Внешний фотоэффект не является единственным. В полупроводниках и диэлектриках наблюдается «внутренний фотоэффект» — электроны под действием поглощенного света отрываются от атомов и приобретают возможность участвовать в создании тока, но не выходят из полупроводника наружу. Квантовый характер этого (более сложного) процесса также выявляется вполне отчетливо.
Если частота света мала, то при его поглощении фотоэффект возникает, но вещество нагревается — растет его внутренняя энергия; конечно, нагревание вещества имеет место и при фото: эффекте.
