Правила по технике безопасности при выполнении лабораторных работ

ОБЩИЕ УКАЗАНИЯ

1. Порядок подготовки и выполнения лабораторных работ

Основная задача физического лабораторного практикума заключается в приобретении навыков проведения физического эксперимента, усвоении методики обработки результатов, закреплении теоретического материала и в исследовательской проверке физических законов.

Целью физического практикума является практическое подтверждение теоретических положений курса физики, углубление и усовершенствование знаний, которые получены студентами на лекции.

Необходимое условие успешного прохождения практикума - своевременное изучение теории. Наилучшего усвоения знаний с наименьшей затратой сил и времени можно добиться, если лекционный материал прорабатывать в тот же день, когда прослушана лекция.

При подготовке к лабораторной работе студенту нужно:

1) выяснить, под каким номером значится его фамилия в лабораторном журнале, и по графику лабораторных работ определить номер очередной работы;

2) в читальном зале библиотеки в тетради для лабораторных работ написать инструкцию к лабораторной работе, используя "Методические указания к лабораторным работам по физике для студентов всех специальностей";

3) повторить теоретический материал по теме работы, используя список литературы, приведенный в "Методических указаниях", осмыслить цель и ход работы. При подготовке теории рекомендуется ответить на контрольные вопросы, которые содержит инструкция.

К лабораторной работе допускаются студенты, получившие допуск к ее выполнению. Необходимым условием готовности является наличие в тетради инструкции к лабораторной работе, а достаточным - знание порядка выполнения работы.

Лабораторная работа считается выполненной, если:

1) сделаны все экспериментальные замеры и заполнены таблицы в лабораторной тетради;

2) выполнены все необходимые расчеты;

3) построены графики исследуемых зависимостей (если это предусмотрено инструкцией к выполнению работы);

4) выполнен расчет погрешностей;

5) записан в лабораторной тетради вывод, содержащий аналитический анализ полученных результатов;

6) результаты расчетов и вывод должны быть предъявлены преподавателю, который делает в журнале отметку о выполнении работы;

7) произведена защита теоретической части работы.

Лабораторные работы защищаются и сдаются на занятии.

Защита лабораторных работ осуществляется каждым студентом индивидуально. Количество баллов, которые можно получить за защиту лабораторной работы, сообщается студентам на первой лекции или лабораторном занятии. Если студент не знает ответа на контрольные вопросы, ему дается дополнительная возможность подготовиться к защите на следующем занятии. Баллы, которые выставляются за лабораторную работу, при этом снижаются. После второй попытки защита лабораторной работы оценивается минимальным баллом. Студент, который не защитил две и больше работы, к выполнению следующей работы не допускается.

Внимание! Ликвидация задолженностей по лабораторным роботам во время занятий не производится. Отработка пропущенных лабораторных работ осуществляется в свободное от занятий время, согласованное с преподавателем.

Измерительные приборы

Штангенциркуль

Штангенциркуль позволяет измерять линейные размеры тел, в частности диаметры внешних и внутренних отверстий. На металлической штанге А (рис. 1) с неподвижной ножкой В на конце нанесена основная шкала - сантиметровые и миллиметровые деления. Вдоль штанги может перемещаться рамка с нониусом С и подвижной ножкой D. Когданожки В и D сталкиваются, нуль линейки и нуль нониуса должны совпадать.

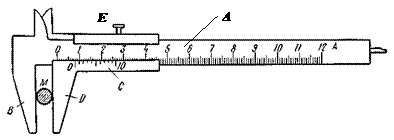Рисунок 1 - Штангенциркуль

Нониус является небольшой подвижной линейкой С со шкалой, количество делений которой m на одно меньше (m-1) количества делений шкалы масштабной линейки А (например, девяти делениям основной шкалы соответствуют десять делений на нониусе).

Если а – цена деления нониуса, b – цена деления масштабной линейки, m- количестводелений на нониусе, то связь между указанными делениями линейки и нониуса следующая:

am = (m-1)b.

Получаемая из этой формулы разность

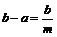
называется точностью нониуса, т.е. точность нониуса b/m равняется отношению цены наименьшего деления масштаба к делению на нониусе. Точность нониуса обычных штангенциркулей равняется 0,1 мм.

При измерении предмет зажимают между ножками, винтом Е фиксируют подвижную рамку и проводят отсчет. Длина измеренного предмета L равняется целому числу k мм масштабной линейки плюс десятые доли числа n. Число n показывает тот номер деления нониуса, который совпадает с некоторым делением масштабной линейки:

.

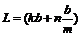Микрометр

Микрометр (рис. 2) служит для измерения диаметров провода, небольшой толщины пластинок и так далее. Он имеет вид тисков, в которых измеряемый объект зажимается с помощью винта.

Ход винта равняется 0,05 мм. На винте расположен барабан В с нанесенной на него шкалой, которая имеет 50 делений. При одном полном обороте барабана его край смещается на 0,50 мм основной шкалы. Поскольку шкала барабана имеет 50 делений, то цена деления этой шкалы равняется 0,01 мм. При завинченом винте нуль барабана стоит против нуля основной шкалы. Основная шкала имеет два масштаба: верхний и нижний. Нижний разбит на сантиметры и миллиметры. Верхний масштаб смещен относительно нижнего на 0,5 мм. Измеряемый предмет помещают между винтом и упором и подводят винт к соприкосновению с предметом. Для создания равномерного давления винта на измеряемый объект микрометр обеспечен специальным приспособлением - трещоткой, которая не допускает очень сильного давления.

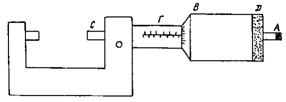
Рисунок 2 - Микрометр

При измерении с помощью микрометра могут наблюдаться два случая:

1) Измеряемый предмет имеет длину, которая равняется а целых миллиметров и несколько сотых долей миллиметра, значения которых лежат в интервале от а до (а+0,50) мм. В этом случае сотые доли миллиметра прямо приписываются к целым мм.

2) Измеряемый предмет имеет длину, которая равняется (а+0,5) целых миллиметров и несколько сотых долей миллиметра, значения которых лежат в интервале от (а+0,50) до (а+1) мм. В этом случае сотые доли миллиметра приписываются к (а+0,5) мм.

Какой из этих случаев имеет место, судят по верхней шкале. Если край барабана стоит ближе к делению нижней основной шкалы, то это первый случай, если же к делению верхней - это второй.

Рычажные весы

Перед взвешиванием нужно проверить "нуль" весов, для этого, повернув ручку аретира левой рукой, "открыть" весы (снять весы с аретира). Если стрелка колеблется в пределах шкалы, весы готовы к работе. При взвешивании на рычажных весах любого типа на левую чашку весов (при закрытых весах) помещают груз, а правой рукой на правую чашку помещают разновесы.

Внимание! Весы снимают с аретира только для того, чтобы выяснить, находятся ли нагруженные чашки в равновесии.

Не отпуская аретира, слегка приоткрывают весы, чтобы выяснить, которая из чашек перевешивает. Потом весы закрывают и изменяют набор гирь. Так повторяют до тех пор, пока не установятся плавные колебания стрелки в пределах шкалы.

Максимальная точность взвешивания на технических весах - 10 миллиграмм.

Гистограмма и ее построение

Пусть есть выборка из n значений измеренной величины. Для того, чтобы получить первое представление о распределении этой величины, строят так называемую гистограмму. Гистограмма это ступенчатый график (диаграмма), для построения которой по оси абсцисс откладывают значение измеренной величины, разбитое на интервалы (бины), а по оси ординат - количество Δn значений этой величины, которые попадают в каждый бин. По оси ординат могут быть отложены также вероятности Δn /n попадания измеренного значения в определенный бин, при этом вид гистограммы не изменится.

Для построения гистограммы необходимо:

1) сделать некоторое количество измерений и в полученной выборке найти минимальное x_min и максимальное x_max значение измеренной величины;

2) найти ширину Δх одного бина, разделив разность (x_max - x_min) на количество бинов, например, на десять:

;

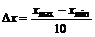3) полученные десять бинов последовательно отложить на оси абсцисс, отмечая начало и конец каждого бина;

4) подсчитать количество значений Δn, которое попадает в каждый бин, и отложить эти числа по оси ординат. Сумма этих чисел должна равняться количеству значений в выборке (рис. 3).

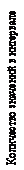Рисунок 3 - Гистограмма

Построив гистограмму, можно сделать вывод о следующих закономерностях процесса измерения, которые обусловлены влиянием случайных погрешностей на значение измеренной величины:

1) наиболее часто встречаются величины, которые близки к среднему значению - они наиболее вероятны;

2) величины, одинаково отличающиеся от среднего значения, встречаются одинаково часто – они равновероятны;

3) величины, значительно отличающиеся от среднего значения, маловероятны.

Если увеличивать объем выборки и уменьшать ширину бинов, то ломаная линия в предельном случае превращается в плавную симметричную кривую, которая имеет вид колокола.

МЕХАНИКА

Лабораторная работа № 101

Порядок выполнения работы

1. Проведя необходимые измерения, снять 40 значений физической величины ( х ). Записать эти значения в тетрадь.

2. Из 40 значений выбрать х_min и x_max. Определить ширину бина Δх.

3. По полученным данным построить гистограмму.

4. Из 40 значений произвольным образом выбрать любые 10 значений, которые идут подряд, и определить погрешность измерений по методике, описанной в разделе 4.5 с доверительной вероятностью Р=0,9.

5. Для тех же 10 выбранных значений определить погрешность измерений, приняв доверительную вероятность Р= 0,95.

6. Результаты расчетов занести в таблицу 1.

7. Из этих же 10 значений измеренной величины выбрать 7 (что также идут подряд) и определить величину погрешности измерений с вероятностью Р=0,9. Результаты также занести в таблицу по форме таблицы 1.

8. Отчет должен содержать вывод о том, как зависит ширина доверительного интервала от величины доверительной вероятности и от числа измерений.

Таблица 1 Результата измерений и вычислений

№, п/п	xi		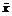		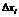	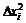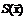P				, %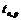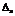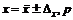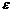
1. 2. ... ... n	х1 х2 хn					0,9	0,95
-	Σ xi	-	-	Σ∆xi2	-	-	-	-	-	-	-	-	-	-	-

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем заключается процесс измерения физической величины? Какие виды измерений Вы знаете? Приведите пример прямых и косвенных измерений.

2. Какие бывают ошибки ? Как они учитываются при измерениях? Приведите примеры.

3. Что такое гистограмма? Как определить ширину интервала (бина) при построении гистограммы?

4. Что такое нормальное распределение или распределение Гауса?

5. Можно ли определить истинное значение измеренной величины?

6. Что называется вероятностью?

7. Что такое надежность или доверительная вероятность?

8. Когда при расчетах погрешностей применяется метод Стьюдента?

9. Как определяется ширина доверительного интервала при расчетах по методу Стьюдента?

10. Как связанна ширина доверительного интервала с доверительной вероятностью?

Лабораторная работа №102

Порядок выполнения работы

1. Измерить длину наклонной плоскости L, ее высоту h, длину основания b.

2. Поместить тело в верхнюю точку наклонной плоскости и проследить его движение по пути AON. Измерить координаты X_m и Y_m точки падения.

3. Вычислить cos α и tg α по формулам:

,

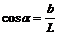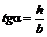
4. Вычислить k для каждого тела, подставив в (4) выражения для моментов инерции тел I.

5. Вычислить значение скорости по формуле (5) и считать ее расчетной, обозначив V_р.

6. Вычислить значение скорости по формуле (12) и считать ее экспериментальной, обозначив V_е.

7. В результате проведения опыта должны получить не меньше трех значений скоростей V_р и V_е (высоту наклонной плоскости в работе необходимо изменять).

8. В отчете по работе все результаты опытов и расчетов должны быть оформлены в виде таблицы 1. В выводе по данной работе необходимо сравнить скорости V_р и V_е для каждого тела, а также проанализировать зависимость скорости тел от их формы и от высоты наклонной плоскости.

Таблица 1 - Результаты измерений и вычислений

Тело

h,м

L,м

b,м

cosα

tgα

k

Xm,м

Ym,м

Vр,м/с

Vэ,м/с

Шар

Сплошной цилиндр

Полый цилиндр

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Тело скатывается по наклонной плоскости. Какие силы и моменты сил обеспечивают скатывание?

2. Что утверждает закон сохранения энергии в механике?

3. Как запишется закон сохранения энергии для тела, которое скатывается по наклонной плоскости к ее подножию?

4. По какой формуле можно рассчитать кинетическую энергию вращательного движения тела?

5. Как связанны между собой линейная и угловая скорости?

6. Как движется тело, брошенное под углом к горизонту?

7. На какие два прямолинейных движения можно разложить движение по параболе вблизи поверхности Земли?

8. Почему движение по оси Y ускоренное, а по оси X равномерное?

9. Как зависят скорости V_х и V_у от времени?

10. Как зависят координаты X и Y от времени?

11. Что характеризует момент инерции?

Лабораторная работа № 103

И СИЛЫ ТРЕНИЯ В ОПОРЕ

Цель работы: Изучение основных закономерностей вращательного движения; определение момента инерции махового колеса и силы трения в опоре.

Приборы и принадлежности: маховое колесо, закрепленное на опоре; рулетка; секундомер; штангенциркуль; груз на нити.

Основные требования к теоретической подготовке:При подготовке к лабораторной работе необходимо проработать разделы курса общей физики "Основной закон динамики вращательного движения", "Закон сохранения энергии для поступательного и вращательного движений" и методические указания к данной работе.

Порядок выполнения работы

1. Измерить с помощью штангенциркуля радиус вала, на который наматывается нить с грузом.

2. Намотать на вал нить с прикрепленным к свободному концу грузом Р массой m. Установить груз на высоте h₁. Высоту отсчитывать от наиболее низкого положения, на которое может опуститься груз.

3. По секундомеру определить время движения груза от верхней точки до низшего положения. Не останавливая груз, определить, какой путь h₂ пройдет груз, поднимаясь вверх по инерции за счет кинетической энергии маховика.

4. Результаты измерений занести в таблицу 1.

5. Пункты 3 и 4 повторить 4-5 раз (меняя начальную высоту h₁ по указанию преподавателя)

6. По формулам (2) и (5) рассчитать силу трения в опоре и момент инерции махового колеса.

7. Рассчитать погрешность измерения одной из двух найденных величин (по указанию преподавателя).

Таблица 1 - Запись результатов измерений и вычислений

№	R,м	m,кг	h1,м	h2,м	t,с	I,кг·м2	f, Н	Результат

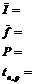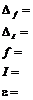КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какой физический смысл момента инерции тела?

2. Чему равняется момент инерции материальной точки и тела?

3. Запишите основной закон динамики для вращательного движения.

4. Какие силы называются консервативными? Какие неконсервативными?

5. Какая механическая система является замкнутой?

6. Какие виды механической энергии Вы знаете? Чему равняется каждая из них?

7. Запишите закон сохранения энергии для данной системы тел при движении груза: только вниз? вниз, а потом вверх?

8. Каким будет характер движения махового колеса при отсутствии трения в опоре?

9. Как определить линейные и угловые кинематические характеристики движения тел в данной работе?

10. Получите формулы для расчета силы трения и момента инерции, используемые в данной работе.

Лабораторная работа № 104

Теоретические сведения

Основное уравнение динамики вращательного движения имеет вид:

,

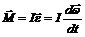где М - результирующий момент сил, которые действуют на тело, Н·м;

I - момент инерции тела, кг·м²;

ε - угловое ускорение этого тела, рад/с²;

ω - угловая скорость, рад/с.

При вращательном движении тела вокруг неподвижной оси направление векторов момента сил и углового ускорения совпадают с осью вращения. В этом случае для проверки основного уравнения достаточно выполнения соотношения для разных значений 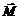и І.

Моментом силыотносительно неподвижной оси называется скалярная величина, которая численно равняется произведению силы F на ее плечо l (кратчайшее расстояние от оси вращения до прямой, вдоль которой действует сила):

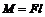
Момент инерции является физической величиной, которая характеризует инертность тела при изменении его угловой скорости под действием вращательного момента.

Момент инерции материальной точки I_i относительно любой оси равняется произведению ее массы m_i на квадрат расстояния r_i до этой оси:

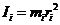
Момент инерции твердого тела I относительно любой оси равняется сумме моментов инерции всех материальных точек тела относительно этой оси:

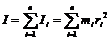
Для любого твердого тела в случае непрерывного распределения массы тела по его объему формула момента инерции относительно оси вращения может быть записана в виде

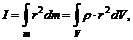
где интегрирование ведется по всему объему тела, ρ – плотность тела.

Если ось вращения не проходит через центр масс тела, то его момент инерции определяется по теореме Штейнера, согласно которой момент инерции тела относительно произвольной оси равняется сумме момента инерции тела I₀ относительно параллельной к ней оси, которая проходит через центр масс, и произведения массы этого тела m на квадрат расстояния d между осями:

.

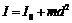Основной закон динамики вращательного движения удобно проверить на маятнике Обербека.

Порядок выполнения работы

1. Ознакомиться с экспериментальной установкой и ее действием.

2. Измерить штангенциркулем радиусы шкивов r₁ и r₂, а линейкой – расстояние от центра крестовины до центра грузов R.

3. На один из шкивов намотать нить в один слой и закрепить на нити груз массой m₁.

4. Выбрать высоту h, с которой будет опускаться груз.

5. Отпуская груз, секундомером измерить время t прохождения грузом расстояния h. Опыт повторить 3-5 раз и усреднить найденные значения времени t.

6. Намотать нить на второй шкив радиусом r₂. Определить время движения груза 3-5 раз и усреднить значение времени.

7. Повторить пункты 5 и 6 с другим грузом m₂.

8. Результаты измерений занести в таблицу 1.

9. Рассчитать ускорение движения груза по формуле (5) и углового ускорения по формуле (7).

10. Рассчитать вращательный момент М₁ по формуле (6) и М₂ по формуле (8).

11. При оформлении результатов лабораторной работы необходимо обратить внимание на результаты расчетов в столбцах 8 и 12 и сделать соответствующие выводы.

Таблица 1 - Результаты измерений и вычислений

№	h, м	R, м	mi, кг	ri, м	t, с	a, м/с2	M1, Н·м	ε, рад/с2	m0, кг	I, кг·м2	M2, Н·м
1	2	3	4	5	6	7	8	9	10	11	12

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое момент инерции точки, момент инерции тела? Что характеризует момент инерции?

2. Теорема Штейнера. В каких случаях момент инерции определяется по теореме Штейнера?

3. Основное уравнение динамики вращательного движения (I=const).

4. Что называется моментом силы? Что такое плечо силы?

5. Что называется угловой скоростью, угловым ускорением?

6. Как связаны угловые и линейные кинематические характеристики?

7. Какие силы действуют на шкив и на груз в лабораторной работе?

8. Как определяется момент силы натяжения нити в работе?

9. Как изменится угловое ускорение маятника Обербека, если изменить положение цилиндров на стрежнях относительно оси.

МОЛЕКУЛЯРНАЯ ФИЗИКА

Лабораторная работа № 201

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ С_p / C_v ДЛЯ ВОЗДУХА

МЕТОДОМ КЛЕМАНА - ДЕЗОРМА

Цель работы: определение отношения теплоемкости воздуха при постоянном давлении к теплоемкости воздуха при постоянном объеме методом Клемана-Дезорма, основанном на исследовании некоторой массы газа, который последовательно переходит в разные состояния.

Приборы и оборудование: закрытый стеклянный баллон, манометр, насос.

Основные требования к теоретической подготовке:При подготовке к лабораторной работе необходимо проработать разделы курса общей физики " Первое начало термодинамики для изопроцессов", и методические указания к данной работе.

Теоретические сведения

Для выполнения лабораторной работы необходимо знать:

1. Первое начало термодинамики утверждает, что количество теплоты, переданное газу, идет на смену его внутренней энергии и на осуществление работы газом против внешних сил

dQ = dU + dW, (1)

где dQ - количество теплоты, Дж;

dU - изменение внутренней энергии, Дж;

dW - работа против внешних сил, Дж.

Работа в термодинамике определяется как

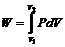, (2)

где Р - давление газа, Па;

dV - изменение объема системы, м³.

2. Число независимых координат, которые полностью определяют положение точки в пространстве, или количество независимых движений, которые может выполнять точка, называется числом степеней свободы.

Молекуле одноатомного газа приписывают три степени свободы поступательного движения. Система, которая состоит из двух атомов, имеет пять степеней свободы, три из них поступательные, а две - вращательные. Трехатомная молекула имеет шесть степеней свободы, из них три поступательные, и три вращательные степени свободы.

3. Закон о равномерном распределении кинетической энергии утверждает, что на каждую поступательную и вращательную степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, которая равняется 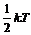. Итак, средняя кинетическая энергия молекулы определяется выражением

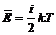, (3)

где Т - термодинамическая температура, К;

i- число степеней свободы;

k - постоянная Больцмана, .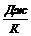

4. Внутренняя энергия U_m одного моля идеального газа соответственно равняется

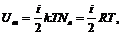(4)

где N_a - число Авогадро, ;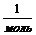

R = kN_a = 8,31 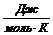- универсальная газовая постоянная

5. Теплоемкостью С тела называется физическая величина, которая численно равняется отношению количества теплоты dQ, которое получает тело, к изменению его температуры dТ в данном термодинамическом процессе:

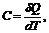(5)

Величина С зависит от массы тела, его химического состава, и процесса, в котором сообщается теплота dQ.

Теплоемкость единицы массы вещества называют удельной теплоемкостью с – величина, которая равняется количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:

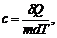(6)

где т – масса газа, кг.

Удельная теплоемкость измеряется в Дж/(кг(К).

Молярной теплоемкостью С_m называется теплоемкость одного моля вещества, т.е. величина, которая равняется количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К:

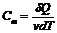, (7)

где v - число молей (количество вещества).

Молярная теплоемкость измеряется в Дж/(моль(К).

Эти теплоемкости связанные между собой соотношением:

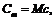(8)

где М – молярная масса вещества.

6.Тепоремкость газа зависит от вида изопроцесса, т.е. от условий. при которых протекает нагревание газа.

Если нагревать газ при постоянном объеме (изохорный процесс), то все тепло, которое получает газ извне, полностью идет на увеличение внутренней энергии. В этом случае dW = 0, и первое начало термодинамики имеет вид:

dQ_V = dU. (9)

Тогда молярная теплоемкость при постоянном объеме

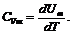(10)

Подставим в формулу (10) выражение (4) для внутренней энергии одного моля идеального газа и получим выражение для молярной теплоемкости газа при постоянном объеме:

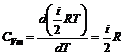. (11)

Если нагревать газ при постоянном давлении (изобарный процесс), то поглощенное тепло идет не только на увеличение внутренней энергии, но и на работу изобарического расширения. Поэтому теплоемкость C_р при постоянном давлении должна быть больше, чем теплоемкость С_V при постоянном объеме. Особенно эти теплоемкости различаются у газов вследствие относительно большого коэффициента объемного расширения.

Для изобарического процесса первое начало термодинамики имеет вид:

dQ = dU + dW , (12)

где dW = PdV.

Тогда, по определению

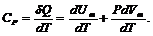(13)

Из уравнения Менделеева-Клапейрона для одного моля выразим величину: PdV_т:

PdV_т = RdT (14)

Подставив у уравнение (13) выражение (4) и (14), получим выражение для молярной теплоемкости при постоянном давлении:

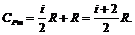(15)

Молярные теплоемкости С_Vт и C_pт связанны уравнением Майера:

С_Рm – С_Vm = R (16)

Суть этого уравнения заключается в том, что при изобарическом нагревании газа на один градус к газу должно быть подведено больше тепла, чем для такого же изохорического нагревания. Уравнение Майера раскрывает физический смысл универсальной газовой постоянной R: она равняется работе, которую совершает 1 моль идеального газа при изобарическом расширении.

Отношение теплоемкостей

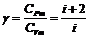(17)

есть величина постоянная для данного газа и принадлежит к числу очень важных термодинамических характеристик.

Порядок выполнения работы

1. Плотно закрыть кран К. Накачать воздух в баллон, разность уровней воды в манометре должна составлять 150-200 мм

2. Когда перемещение уровней воды в коленах манометра остановится, сделать отсчет разности уровней, записать в таблицу значения Н.

3. Быстро открыть кран К и, как только уровни жидкости в манометре сравняются (давление уменьшилось до атмосферного), закрыть его.

4. После установления давления в баллоне провести отсчет разности уровней в коленах манометра h. Все результаты измерений записать в таблицу 1.

5. Опыт повторить 3-5 раза.

6. Рассчитать теоретическое значение g_теор. для воздуха, считая его двухатомным газом, по формуле (17).

7. По формуле (23) вычислить γ. Оценить ошибку методом Стьюдента.

8. Выводы отчета должны содержать результаты сравнения расчетной величины g по результатам эксперимента и g_теор. для воздуха.

Таблица 1 - Результаты измерений и вычислений

№ пп

Н, мм

h, мм

g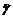

Dg

(Dg)2

S

P

tP,n

D

e,%

g ±∆;

gтеор

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется теплоемкостью?

2. Что называется удельной теплоемкостью?

3. Связь между удельной и молярной теплоемкостями.

4. Физический смысл универсальной газовой постоянной.

5. Дать определения всех изопроцессов.

6. Какой процесс называется адиабатическим?

7. Что называется внутренней энергией системы?

8. Записать первое начало термодинамики для изопроцессов.

9. Какой процесс описывает уравнение Пуассона?

10. Как определить значение молярных теплоемкостей для разных газов?

11. Что происходит с внутренней энергией газа при его адиабатическом, изотермическом и изобарическом сжатиях?

12. Что называется степенью свободы молекулы?

Лабораторная работа № 202

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ

МЕТОДОМ СТОКСА

Цель работы:: определение коэффициента вязкости (внутреннего трения) жидкости методом Стокса по скорости падения шарика.

Приборы и оборудование: прибор Стокса,секундомер, линейка, микрометр.

Основные требования к теоретической подготовке:При подготовке к лабораторной работе необходимо проработать разделы курса общей физики " Основные положения МКТ", и методические указания к данной работе.

Порядок выполнения работы

1. Микрометром измерить диаметр шарика (не меньше 3 раз). Полученные данные занести в таблицу 1.

2. Опустить шарик в жидкость сквозь воронку. Глаз наблюдателя должен находиться напротив верхней метки так, чтобы она сливалась в одну прямую.

3. Измерить время движения шарика от верхней метки до нижней. Полученные данные занести в таблицу 1.

4. Масштабной линейкой измерить расстояние между метками. АВ.

5. Определить коэффициент вязкости h.

6. Опыт повторить 4-7 раз с другими шариками.

7. Результаты измерений и вычислений занести в таблицу 1.

8. Рассчитать погрешность определения h методом Стьюдента

Таблицв 1. Результаты измерений и вычислений

№

l,м

r, кг/м3

rж, кг/м3

r, м

t, с

h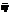, Па×с

, Па×с

Dh,

(Dh)2

S

P

t

D

e%

hіст, Па×с

контрольные вопросы

1. Основные положения молекулчрно-кинетической теории.
2. Написать уравнение Стокса.
3. Как движется шарик с момента п