Интерференция когерентных волн. Амплитуда результирующего колебания при интерференции двух волн, условия максимумов и минимумов амплитуды. Интерференционный спектр.

Интерференция волн — взаимное усиление или ослабление амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве. Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

Интерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них не ортогональны. Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера.

При интерференции энергия волн перераспределяется в пространстве. Это не противоречит закону сохранения энергии потому, что в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн.

При наложении некогерентных волн средняя величина квадрата амплитуды результирующей волны равна сумме квадратов амплитуд накладывающихся волн. Энергия результирующих колебаний каждой точки среды равна сумме энергий ее колебаний, обусловленных всеми некогерентными волнами в отдельности.

Амплитуда результирующего колебания максимальна и равна сумме амплитуд слагаемых колебаний: если разность фаз этих колебаний составляет четное число «Пи»; если же разность фаз составляет нечетное число «Пи», то амплитуда результирующего колебания минимальна и равна разности амплитуд слагаемых колебаний.

В физических экспериментах спектры обычно получают, пропуская «свет» либо сквозь призму, либо сквозь узкие щели или крошечные отверстия в плотном материале. На основании способа получения спектры бывают призматические и интерференционные. Спектр – это видимый на экране ряд из шести цветов, плавно переходящих один.

3.8 Осуществление интерференции света с помощью тонкой пленки. Интерференционные полосы равного наклона и равной толщины.

Интерференция света в тонких плёнках

Интерференция в тонкой плёнке. Альфа — угол падения, бета — угол отражения, жёлтый луч отстанет от оранжевого, они сводятся глазом в один и интерферируют.

Получить устойчивую интерференционную картину для света от двух разделённых в пространстве и независящих друг от друга источников света не так легко, как для источников волн на воде. Атомы испускают свет цугами очень малой продолжительности, и когерентность нарушается. Сравнительно просто такую картину можно получить, сделав так, чтобы интерферировали волны одного и того же цуга. Так, интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённых объективов. Луч света, проходя через плёнку толщиной , отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, от чего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при , где — длина волны. Если нм, то толщина плёнки равняется 550:4=137,5 нм.

Лучи соседних участков спектра по обе стороны от нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей

— условие максимума;

— условие минимума,

где k=0,1,2... и — оптическая длина пути первого и второго луча, соответственно.

Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек, в цветах побежалости, и т. д.

Полосы равной толщины и равного наклона. 1. Полосы равного наклона (интерференция от плоскопараллельной пластинки). Интерференционная картина в плоскопараллельных пластинках (пленках) определяется величинами . Для данных каждому наклону i лучей соответствует своя интерференционная полоса.

Интерференционные полосы, возникающие в результате наложения лучей падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона. Лучи 1' и 1”, отразившиеся от верхней и нижней граней пластинки, параллельные друг другу, так как пластинка плоскопараллельна. Следовательно, интерферирующие лучи 1' и 1” «пересекаются» только в бесконечности. Для их наблюдения используют собирающую линзу и экран (Э), расположенный в фокальной плоскости линзы. Параллельные лучи 1' и 1” соберутся в фокусе F линзы , в эту же точку придут и другие лучи, параллельные лучу 1, в результате чего увеличивается общая интенсивность. Лучи 3, наклоненные под другим углом , соберутся в другой точке Р фокальной плоскости линзы. Если оптическая ось линзы перпендикулярна поверхности пластинки, полосы равного наклона будут иметь вид концентрических колец с центром в фокусе линзы. 2. Полосы равной толщины (интерференция от пластинки переменной толщины). Пусть на клин (угол между боковыми гранями мал) падает плоская волна, направление распространения которой совпадают с параллельными лучами 1и 2. Из всех лучей, на которые разделяется падающий луч, рассмотрим лучи 1' и 1”,. отразившиеся от верхней и нижней поверхностей клина. При определенном взаимном положении клина и линзы лучи 1' и 1” пересекутся в некоторой точке А, являющейся изображением точки В. Т.к. 1' и 1” когерентны, они будут интерферировать.

Если источник расположен довольно далеко от поверхности клина, и угол достаточно мал, то оптическая разность хода между интерферирующими лучами 1' и 1” может быть с достаточной степенью точностью вычислена по ф-ле. , где в качестве d берется толщина клина в месте падения на него луча.. Лучи 2' и 2'', образовавшиеся за счет деления луча 2, падающего на другую точку клина, собираются линзой в точке А'. Оптическая разность хода уже определяется толщиной d'.Таким образом, на экране возникает система интерференционных полос. Каждая из полос возникает за счет отражения от мест пластинки, имеющих одинаковую толщину (в общем случае толщина пластинки может изменяться произвольно). Интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, называются полосами равной толщины.

3.9 Стоячая волна как частный случай интерференции. Уравнение плоской стоячей волны.Амплитуда, узлы и пучности стоячей волны. Превращения энергии в стоячей волне. Стоячие волны в сплошных ограниченных средах. Условия возникновения стоячей волны в стержне, в столбе воздуха, в натянутой струне.

Стоячие волны как результат интерференции

Cтоячие волны — частный случай интерференции. Стоячие волны образуются в результате наложения двух волн одинаковой амплитуды, фазы и частоты, распространяющихся в противоположных направлениях.

Амплитуда в пучностях стоячей волны равна удвоенной амплитуде каждой из волн. Поскольку интенсивность волны пропорциональна квадрату ее амплитуды, это означает, что интенсивность в пучностях в 4 раза больше интенсивности каждой из волн или же в 2 раза больше суммарной интенсивности двух волн. Здесь нет нарушения закона сохранения энергии, поскольку в узлах интенсивность равна нулю.

Уравнение плоской стоячей волны:

Амплитуда стоячей волны: А=2А₀ |sin2пx/λ|

Как видим, амплитуда стоячей волны зависит от координаты x. Знак модуля означает, что амплитуда — всегда положительна.

Стоячая волна не переносит энергию. Дважды за период происходит превращение энергии стоячей волны то полностью в потенциальную, сосредоточенную в основном вблизи узлов волны, то полностью в кинетическую, сосредоточенную в основном вблизи пучностей волны. В результате происходит переход энергии от каждого узла к соседним пучностям и обратно. Средний по времени поток энергии в любом сечении волны равен нулю.

При изучении кинематики и динамики вращательного движения следует обратить внимание на связь между угловыми и линейными характеристиками. Здесь вводятся понятия момента силы, момента инерции, момента импульса и рассматривается закон сохранения момента импульса

Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов.

Трубка Кундта является простым приспособлением для демонстрации стоячих звуковых волн. Трубка Кундта представляет собой длинную стеклянную трубку, в которой насыпано немного легкого порошка (например пробковой пыли). Один конец трубки запаян, в другом с помощью пробки укреплен медный стержень. Если потереть стержень наканифоленной замшей, то он начнет скрипеть, а пыль расположится аккуратными кучками вдоль трубки. Такое распределение обусловлено стоячими звуковыми волнами.

Рассмотренные в предыдущем параграфе случаи возникновения в стержне стоячих волн значительной амплитуды при заданном гармоническом движении одного из концов стержня представляют собой не что иное, как явление резонанса в сплошной системе.

Как мы убедились, если бы потери энергии в стержне отсутствовали, то при определенных значениях частоты этой внешней силы амплитуда стоячих волн в стержне возрастала бы до бесконечности.

И действительно, сопоставив, с одной стороны, условия, определяющие частоты внешней силы, при которых амплитуды стоячих волн в стержне достигают максимального значения, а с другой — условия, определяющие частоты нормальных колебаний стержня (§ 149), мы позднее убедимся, что те и другие условия совпадают.

Только предполагая, что при распространении и отражении волны потерь энергии не происходит, мы пришли к выводу, что падающая и отраженная волны имеют одинаковую амплитуду и несут с собой одинаковую энергию в противоположных направлениях; в результате наложения этих двух волн энергия не должна течь по стержню, во всяком случае после того, как стоячая волна в стержне уже установилась (при установлении стоячей волны картина течения энергии получается более сложной, и мы не будем ее рассматривать).

Так как амплитуды падающей и отраженной волн в этом случае зависят от х (расстояния от начала стержня), то мы их будем обозначать соответственно через Xt (x) и Х2 (х), причем Х1 > Х2 и Хг есть убывающая, a Xz — возрастающая функция х.

Когда амплитуды двух волн, распространяющихся в противоположных направлениях, везде одинаковы, то Этиплитуды стоячей волны в пучностях, как мы видели, равны удвоенной амплитуде двух волн и одинаковы во всех пучностях.

Этот вывод подтверждает справедливость тех представлений, из которых мы исходили выше при обсуждении вопроса о величине амплитуды стоячих волн в пучности для случая стержня, один конец которого совершает заданное движение.

Учтя все сказанное, мы можем констатировать, что частоты нормальных колебаний стержня и частоты действующей на стержень внешней силы, при которых амплитуды стоячих волн в пучностях достигают максимума, при аналогичных краевых условиях совпадают: при одинаковых краевых условиях на обоих концах стержня на длине стержня должно укладываться целое число полуволн, а при разных краевых условиях на обоих концах стержня — нечетное число четвертей волн.

Итак, мы убедились, что возникновение в стержне под действием гармонической внешней силы стоячих волн значительной амплитуды представляет собой явление резонанса: внешняя сила поддерживает сильные вынужденные колебания, частота и распределение амплитуд которых очень близки к частоте и распределению амплитуд одного из нормальных колебаний стержня.

Именно, в § 149 мы полагали, что распределение амплитуд нормальных колебаний должно быть либо синусоидальным, либо косинусоидальным; теперь мы можем это положение считать обоснованным, поскольку мы убедились (в § 154), что распределение амплитуд стоячих волн действительно является синусоидальным или косинусоидальным, а значит, таким же оно должно быть для нормальных колебаний.

Поэтому наряду со стоячими волнами в системе принципиально должны существовать и бегущие волны (хотя при малых потерях амплитуда этих последних мала по сравнению с амплитудой стоячих волн).

При скорости распространения упругих волн в стержне у~5-105 см/сек длине волны А, = = 1 -Ю"8 см соответствует частота колебаний v= y-jTfg" — 5- 1013 гц.

3.10 Дифракция волн. Объяснение дифракции волн на основе принципа Гюйгенса-Френеля. Дифракция Фраунгофера на одной щели и на дифоакционной решетке.

Отклонение от прямолинейного распространения волн,огибание волнами препятствий называется дифракцией. Дифракция присуща любому волновому процессу в той же мере,как и интерференция. Следствия дифракции: проникновение света в область геометрической тени; образование интерференционной картины.

Явление дифракции волн на поверхности воды можно наблюдать,если поставить на пути волн экран с узкой щелью,размеры которой меньше длины волны. Хорошо будет видно что за экраном распр круговая волна, как если бы в отверстии экрана располаг колеблющееся тело-источник волн. Согласно принципу Гюйгенса так и должно быть. Вторичные источники в узкой щели располаг столь близко др к др что их можно рассматривать как один точечный источник. Если размеры щели велики по сравнению с длиной волны, то картина распространения волн з0а экраном совершенно иная. Волна проходит сквозь щель, почти не меняя своей формы. Только по краям можно заиетить небольшие искривления волновой пов-ти благодаря которым волна частично проникает и в простр-во за экраном. Принцип Гюйгенса в его первоначальной формулировке позволяет понять почему происходит дифракция. Вторичные волны,испуск участками среды проникают за края препятствия, расположенного на пути распространения волны. Однако, исходя из приведенной выше формулировки принципа Гюйгенса, нельзя было объяснить дифракцию во всех деталях. Этот принцип нуждался в уточнении, которое и было сделано франц ученым Френелем волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.

Другой тип дифракции — дифракция Фраунгофера (Й. Фраунгофер, 1787—1826), наблюдаемая в параллельных лучах (плоские волны),— имеет место, если точка наблюдения (иногда и источник света) бесконечно удалена от препятствия, на котором происходит дифракция. Практически это достигается наблюдением дифракционной картины в фокальной плоскости собирающей линзы, расположенной за препятствием. При этом освещенность может быть сделана гораздо больше, чем при дифракции Френеля, благодаря чему дифракция Фраунгофера имеет большое практическое применение. Для наблюдения дифракции Фраунгофера необходимо точечный источник поместить в фокусе собирающей линзы, а дифракционную картину можно исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

Пусть монохроматическая волна падает нормально плоскости бесконечно длинной узкой щели ( 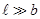), 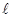- длина, b - ширина. Разность хода между лучами 1 и 2 в направлении φ

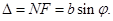Разобьём волновую поверхность на участке щели МN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой полосы выбирается так, чтобы разность хода от краев этих зон была равна λ/2, т.е. всего на ширине щели уложится 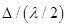зон. Т.к. свет на щель падает нормально, то плоскость щели совпадает с фронтом волны, следовательно, все точки фронта в плоскости щели будут колебаться синфазно. Амплитуды вторичных волн в плоскости щели будут равны, т.к. выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения. Число зон Френеля 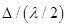укладывающихся на ширине щели, зависит от угла φ.

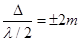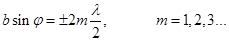Условие минимума при дифракции Френеля: Если число зон Френеля четное или то в т. Р наблюдается дифракционный минимум.

Условие максимума:Если число зон Френеля нечетное 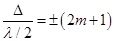или 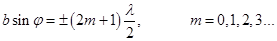то наблюдается дифракционный максимум.

При φ’=0, Δ = 0 в щели укладывается одна зона Френеля и, следовательно, в т. Р главный (центральный) максимум нулевого порядка. Сужение щели приводит к уширению главного максимума и уменьшению его яркости (то же и с другими максимумами). При уширении щели (b>λ) максимумы будут ярче, но дифракционные полосы становятся уже, а числе самих полос - больше. При b>> λ центре получается резкое изображение источника света, т.е. имеет место прямолинейное распространение света.При падении белого света будет разложение на его составляющие. При этом фиолетовый свет будет отклоняться меньше, синий - больше и т.д., красный - максимально. Главный максимум в этой случае будет белого цвета. Как следует из формулы дифракционной решетки sin α = λ / b. положение главных максимумов (кроме нулевого) зависит от длины волны λ. Поэтому решетка способна разлагать излучение в спектр, то есть она является спектральным прибором. Если на решетку падает немонохроматическое излучение, то в каждом порядке дифракции (т. е. при каждом значении m) возникает спектр исследуемого излучения, причем фиолетовая часть спектра располагается ближе к максимуму нулевого порядка. На рис. 6.10.6 изображены спектры различных порядков для белого света. Максимум нулевого порядка остается неокрашенным. С помощью дифракционной решетки можно производить очень точные измерения длины волны.

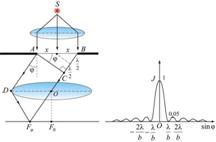
Разобьем щель на зоны Френеля так, чтобы оптическая разность хода между лучами, идущими от соседних зон, была равна .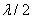

Если на ширине щели укладывается четное число таких зон, то в точке 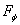(побочный фокус линзы) будет наблюдаться минимум интенсивности, а если нечетное число зон, то максимум интенсивности:

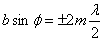– условие минимума интенсивности;

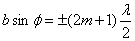– условие максимума интенсивности

Картина будет симметричной относительно главного фокуса точки 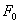. Знак плюс и минус соответствует углам, отсчитанным в ту или иную сторону.

Интенсивность света 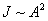. Как видно из рис. 9.5, центральный максимум по интенсивности превосходит все остальные.

Рассмотрим влияние ширины щели.

Т.к. условие минимума имеет вид 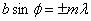, отсюда

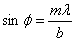
Из этой формулы видно, что с увеличением ширины щели b положения минимумов сдвигаются к центру, центральный максимум становится резче.

При уменьшении ширины щели b вся картина расширяется, расплывается, центральная полоска тоже расширяется, захватывая все большую часть экрана, а интенсивность ее уменьшается.

Дифракция света на дифракционной решетке

Одномерная дифракционная решетка представляет собой систему из большого числа N одинаковых по ширине и параллельных друг другу щелей в экране, разделенных также одинаковыми по ширине непрозрачными промежутками (рис. 9.6).

Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

Обозначим: b – ширина щели решетки; а – расстояние между щелями; 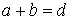– постоянная дифракционной решетки.

Линза собирает все лучи, падающие на нее под одним углом и не вносит никакой дополнительной разности хода.

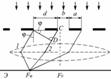
Пусть луч 1 падает на линзу под углом φ (угол дифракции). Световая волна, идущая под этим углом от щели, создает в точке 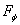максимум интенсивности. Второй луч, идущий от соседней щели под этим же углом φ, придет в ту же точку . Оба эти луча придут в фазе и будут усиливать друг друга, если оптическая разность хода будет равна mλ: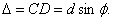

Условие максимума для дифракционной решетки будет иметь вид:

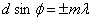где m = ± 1, ± 2, ± 3, … .

Максимумы, соответствующие этому условию, называются главными максимумами. Значение величины m, соответствующее тому или иному максимуму называется порядком дифракционного максимума.

В точке F0 всегда будет наблюдаться нулевой или центральный дифракционный максимум.

Так как свет, падающий на экран, проходит только через щели в дифракционной решетке, то условие минимума для щели и будет условием главного дифракционного минимума для решетки: .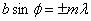

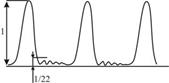
Конечно, при большом числе щелей, в точки экрана, соответствующие главным дифракционным минимумам, от некоторых щелей свет будет попадать и там будут образовываться побочные дифракционные максимумы и минимумы (рис. 9.7). Но их интенсивность, по сравнению с главными максимумами, мала (≈ 1/22).

При условии ,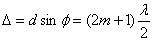

волны, посылаемые каждой щелью, будут гаситься в результате интерференции и появятся дополнительные минимумы.

Количество щелей определяет световой поток через решетку. Чем их больше, тем большая энергия переносится волной через нее. Кроме того, чем больше число щелей, тем больше дополнительных минимумов помещается между соседними максимумами. Следовательно, максимумы будут более узкими и более интенсивными (рис. 9.8).

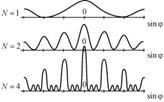
Из (9.4.3) видно, что угол дифракции пропорционален длине волны λ. Значит, дифракционная решетка разлагает белый свет на составляющие, причем отклоняет свет с большей длиной волны (красный) на больший угол (в отличие от призмы, где все происходит наоборот).

Это свойство дифракционных решеток используется для определения спектрального состава света (дифракционные спектрографы, спектроскопы, спектрометры).