Закон Ома для замкнутой цепи.

В § 46 мы познакомились с законом Ома для участка цепи, позволяющим вычислить ток, если известно сопротивление участка и напряжение на его концах. Очень часто, однако, приходится решать задачи, в которых напряжение на концах участка цепи не задано, но зато известны сопротивления всех частей цепи и э. д. с. источника, питающего цепь. Как найти в этом случае силу тока?
Рассмотрим всю замкнутую электрическую цепь, включая и источник тока, и выясним на опыте, от чего зависит ток в этой цепи. Замкнем источник тока, например элемент Даниеля (§75), на внешнюю цепь, содержащую амперметр и реостат, и будем перемещать движок реостата, меняя тем самым сопротивление внешней цепи. Мы обнаружим, что с уменьшением сопротивления внешней цепи ток будет увеличиваться.
Установим теперь реостат так, чтобы сопротивление внешней цепи было незначительным, и будем изменять глубину погружения цинковой пластины элемента. Ток будет увеличиваться по мере погружения пластины.
Для понимания этого результата вспомним, что напряжение на разомкнутом элементе, т. е. его э. д. с, совершенно не зависит от геометрических размеров и формы элемента (§76). Следовательно, при изменении глубины погружения пластины э: д. с. источника не меняется. В чем же причина изменения тока? В § 76 мы видели, что ток идет как по внешней цепи, так и внутри источника. Но сам источник представляет тоже определенное сопротивление току. Это сопротивление носит название внутреннего сопротивления источника. В гальванических элементах оно слагается из сопротивления его электродов и главным образом из сопротивления столба электролита между ними. Погружая цинковую пластину на различную глубину, мы изменяем сечение этого столба и вместе с ним внутреннее сопротивление элемента. Мы видим, что сила тока зависит также от внутреннего сопротивления источника тока.
Полную цепь можно рассматривать как последовательное соединение сопротивления внешней цепи и внутреннего сопротивления источника тока. Полное сопротивление цепи представляет собой сумму внутреннего сопротивления источника и сопротивления внешней цепи. Заменим элемент каким-либо другим, имеющим такое же внутреннее сопротивление, но другую э. д. с. Мы обнаружим, что ток при этом изменится.
Таким образом, ток в цепи зависит от э. д. с. источника и от полного сопротивления цепи.

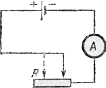
Рис. 126. Измерение тока в цепи при изменении внутреннего сопротивления элемента
Количественный закон, связывающий эти величины, представляет закон Ома для замкнутой цепи: ток в цепи, содержащей источник тока, прямо пропорционален э. д. с. источника и обратно пропорционален полному сопротивлению цепи.
Если обозначить э. д. с. источника через ξ, его внутреннее сопротивление через r, сопротивление внешней цепи через R, а ток через I, то закон Ома представится следующей формулой:
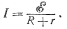(80.1)
Мы видим, что ток, который способен дать источник, зависит не только от э. д. с. источника и сопротивления внешней цепи, но еще и от внутреннего сопротивления. Сказанное относится, конечно, не только к гальваническим элементам, но и к любым источникам тока, например к аккумуляторам или генераторам постоянного тока.

Исто́чник то́ка (также генератор тока) — двухполюсник, который создаёт ток 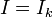, не зависящий от сопротивления нагрузки, к которой он присоединён.

Применение

Реальные генераторы тока имеют различные ограничения (например по напряжению на его выходе), а также нелинейные зависимости от внешних условий. Например, реальные генераторы тока создают электрический ток только в некотором диапазоне напряжений, верхний порог которого зависит от напряжения питания источника. Таким образом, реальные источники тока имеют ограничения по нагрузке.

Источники тока широко используются в аналоговой схемотехнике, например, для питания измерительных мостов, для питания каскадовдифференциальных усилителей, в частности операционных усилителей.

Концепция генератора тока используется для представления реальных электронных компонентов в виде эквивалентных схем. Для описания активных элементов для них вводятся эквивалентные схемы, содержащие управляемые генераторы:

§ Источник тока, управляемый напряжением (сокращенно ИТУН)

§ Источник тока, управляемый током (сокращенно ИТУТ)

Билет 8:Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

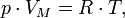
где

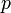§ — давление,

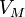§ — молярный объём,

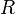§ — универсальная газовая постоянная

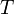§ — абсолютная температура,К.

Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объёмили температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический,энтропии — изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма и адиабата соответственно. Изопроцессы являются частными случаями политропного процесса.

Изобарный процесс

Изобарный процесс (др.-греч. ισος, isos — «одинаковый» + βαρος, baros — «вес») — процесс изменения состояния термодинамической системы при постоянном давлении ( )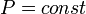

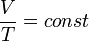
Зависимость объёма газа от температуры при неизменном давлении была экспериментально исследована в 1802 году Жозефом Луи Гей-Люссаком. Закон Гей-Люссака: При постоянном давлении и неизменных значениях массы газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.

Изохорный процесс

Изохорный процесс (от греч. хора — занимаемое место) — процесс изменения состояния термодинамической системы при постоянном объёме ( 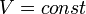). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:

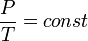
Линия, изображающая изохорный процесс на диаграмме, называется изохорой.

Ещё стоит указать что поданная к газу энергия расходуется на изменение внутренней энергии то есть Q = 3* ν*R*T/2=3*V*ΔP, где R — универсальная газовая постоянная, ν количество молей в газе, T температура в Кельвинах, V объём газа, ΔP приращение изменения давления. а линию, изображающая изохорный процесс на диаграмме, в осях Р(Т), стоит продлить и пунктиром соединить с началом координат, так как может возникнуть недопонимание.

[править]Изотермический процесс

Основная статья: Изотермический процесс

Изотермический процесс (от греч. «термос» — тёплый, горячий) — процесс изменения состояния термодинамической системы при постоянной температуре ( 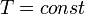)( )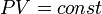. Изотермический процесс описывается законом Бойля — Мариотта:

При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.

Изоэнтропийный процесс

Изоэнтропийный процесс — процесс изменения состояния термодинамической системы при постоянной энтропии ( 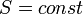). Изоэнтропийным является, например, обратимый адиабатический процесс: в таком процессе не происходит теплообмена с окружающей средой. Идеальный газ в таком процессе описывается следующим уравнением:

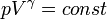
где 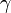— показатель адиабаты, определяемый типом газа.

Билет 9: Я́дерная реа́кция — процесс образования новых ядер или частиц при столкновениях ядер или частиц. Впервые ядерную реакцию наблюдал Резерфорд в 1919 году, бомбардируя α-частицами ядра атомов азота, она была зафиксирована по появлению вторичныхионизирующих частиц, имеющих пробег в газе больше пробега α-частиц и идентифицированных как протоны. Впоследствии с помощью камеры Вильсона были получены фотографии этого процесса.

По механизму взаимодействия ядерные реакции делятся на два вида:

§ реакции с образованием составного ядра, это двухстадийный процесс, протекающий при не очень большой кинетической энергиисталкивающихся частиц (примерно до 10 МэВ).

§ прямые ядерные реакции, проходящие за ядерное время, необходимое для того, чтобы частица пересекла ядро. Главным образом такой механизм проявляется при больших энергиях бомбардирующих частиц.

Если после столкновения сохраняются исходные ядра и частицы и не рождаются новые, то реакция является упругим рассеянием в поле ядерных сил, сопровождается только перераспределением кинетической энергии и импульса частицы и ядра-мишени называется потенциальным рассеянием.

Составное ядро

Теория механизма реакции с образованием составного ядра была разработана Нильсом Бором в 1936 году^[3] совместно с теориейкапельной модели ядра и лежит в основе современных представлений о большой части ядерных реакций.

Согласно этой теории ядерная реакция идёт в два этапа. В начале исходные частицы образуют промежуточное (составное) ядро за ядерное время, то есть время, необходимое для того, чтобы частица пересекла ядро, примерно равное 10⁻²³ — 10⁻²¹с. При этом составное ядро всегда образуется в возбуждённом состоянии, так как оно обладает избыточной энергией, привносимой частицей в ядро в виде энергии связи нуклона в составном ядре и части его кинетической энергии, которая равна сумме кинетической энергии ядра-мишени с массовым числом 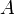и частицы в системе центра инерции.

Энергия возбуждения

Энергия возбуждения 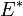составного ядра, образовавшегося при поглощении свободного нуклона, равна сумме энергии связи 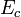нуклона и части его кинетической энергии :

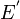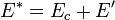
Чаще всего вследствие большой разницы в массах ядра и нуклона примерно равна кинетической энергии бомбардирующего ядро нуклона.

В среднем энергия связи равна 8 МэВ, меняясь в зависимости от особенностей образующегося составного ядра, однако для данных ядра-мишени и нуклона эта величина является константой. Кинетическая же энергия бомбардирующей частицы может быть какой угодно, например при возбуждении ядерных реакций нейтронами, потенциал которых не имеет кулоновского барьера, значение 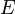может быть близким к нулю. Таким образом, энергия связи является минимальной энергией возбуждения составного ядра^[1][2].

]Каналы реакций

Переход в невозбуждённое состояние может осуществляться различными путями, называемыми каналами реакции. Типы и квантовое состояние налетающих частиц и ядер до начала реакции определяют входной канал реакции. После завершения реакции совокупность образовавшихся продуктов реакции и их квантовых состояний определяет выходной канал реакции. Реакция полностью характеризуется входным и выходным каналами.

Каналы реакции не зависят от способа образования составного ядра, что может быть объяснено большим временем жизни составного ядра, оно как бы «забывает» каким способом образовалось, следовательно образование и распад составного ядра можно рассматривать как независимые события. К примеру 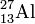может образоваться как составное ядро в возбуждённом состоянии в одной из следующих реакций:

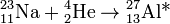
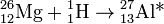
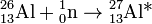
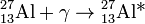
Впоследствии, при условии одинаковой энергии возбуждения, это составное ядро может распасться путём, обратным любой из этих реакций с определённой вероятностью, не зависящей от истории возникновения этого ядра. Вероятность же образования составного ядра зависит от энергии и от сорта ядра-мишени^[2].

Прямые ядерные реакции

Течение ядерных реакций возможно и через механизм прямого взаимодействия, в основном такой механизм проявляется при очень больших энергиях бомбардирующих частиц, когда нуклоны ядра можно рассматривать как свободные. От механизма составного ядра прямые реакции отличаются прежде всего распределением векторовимпульсов частиц-продуктов относительно импульса бомбардирующих частиц. В отличие от сферической симметрии механизма составного ядра для прямого взаимодействия характерно преимущественное направление полёта продуктов реакции вперёд относительно направления движения налетающих частиц. Распределения по энергиям частиц-продуктов в этих случаях также различны. Для прямого взаимодействия характерен избыток частиц с высокой энергией. При столкновениях с ядрами сложных частиц (то есть других ядер) возможны процессы передачи нуклонов от ядра к ядру или обмен нуклонами. Такие реакции происходят без образования составного ядра и им присущи все особенности прямого взаимодействия^[1].

Сечение ядерной реакции

Вероятность реакции определяется так называемым ядерным сечением реакции. В лабораторной системе отсчёта (где ядро-мишень покоится) вероятность взаимодействия в единицу времени равна произведению сечения (выраженного в единицах площади) на поток падающих частиц (выраженный в количестве частиц, пересекающих за единицу времени единичную площадку). Если для одного входного канала могут осуществляться несколько выходных каналов, то отношения вероятностей выходных каналов реакции равно отношению их сечений. В ядерной физике сечения реакций обычно выражаются в специальных единицах — барнах, равных 10⁻²⁴ см².

Выход реакции

Число случаев реакции, отнесённое к числу бомбардировавших мишень частиц 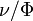называется выходом ядерной реакции. Эта величина определяется на опыте при количественных измерениях. Поскольку выход непосредственно связан с сечением реакции, измерение выхода по сути является измерением сечения реакции^[1][2].

В Я.р. строго выполняются законы сохранения импульса и энергии. Однако нек-рая часть икнетич. энергии может переходить в энергию покоя (см. Масса покоя) и, наоборот, энергия покоя может освобождаться в виде кинетич. энергии [как в реакции (1)], к-рая передается др. частицам при последующих столкновениях или уносится такими элементарными частицами, как фотоны и нейтрино. Энергетическим выходом реакции Q наз. разность между суммарными энергиями покоя всех частиц до и после Я.р. Если Q >0, то суммарная энергия покоя уменьшается в процессе Я.р. Такие Я.р. наз. экзоэнергетическими или беспороговыми. В принципе они могут протекать при сколь угодно малой начальной кинетич. энергии частиц. Наоборот, при Q <0 часть исходной кинетич. энергии частиц превращается в энергию покоя. Такие Я.р. наз. эндоэнергетическими или пороговыми. Для их протекания необходимо, чтобы кинетич. энергия частиц превышала нек-рую величину (порог реакции).

Закон сохранения импульса накладывает ограничение на величину кинетич. энергии, к-рая может перейти в энергию покоя. Вся кинетич. энергия может перейти в энергию покоя лишь в том случае, когда полный импульс реагирующих частиц равен нулю. Поэтому Я.р. удобно рассматривать в системе координат, в к-рой центр инерции (ц.и.) взаимодействующих частиц покоится, т.е. полный импульс равен нулю по определению. Далее, если особо не оговорено, под энергией взаимодействия будет подразумеваться кинетич. энергия частиц в системе ц.и. В случае двух нерелятивистских ат. Я энергия взаимодействия определяется по ф-ле
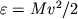, (2)
где 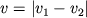- относительная скорость частиц, а M - приведенная масса
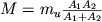, (3)
причем A¹ и A² - массы Я, измеренные в а.е.м. (A¹u).

Условие протекания эндоэнергетических Я.р. можно записать в виде 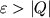. Из этого неравенства с помощью (2) можно получить в лабораторной системе координат, где, напр., частица с массой m² покоится, а частица с массой m¹ налетает на нее с кинетич. энергией 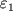, необходимое условие для протекания эндоэнергетической реакции:
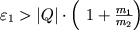. (4)
Такое возрастание порога реакции в лабораторной системе координат объясняется тем, что часть кинетич. энергии, связанная с движением центра масс, остается бесполезной для Я.р.

Я́дерный реа́ктор — это устройство, в котором осуществляется управляемая цепная ядерная реакция, сопровождающаяся выделением энергии. Первый ядерный реактор построен и запущен в декабре 1942 года в СШАпод руководством Э. Ферми. Первым реактором, построенным за пределами США, стал ZEEP, запущенный вКанаде в сентябре 1945 года^[1]. В Европе первым ядерным реактором стала установка Ф-1, заработавшая 25 декабря 1946 года в Москве под руководством И. В. Курчатова.^[2]

К 1978 году в мире работало уже около сотни ядерных реакторов различных типов. Составными частями любого ядерного реактора являются: активная зона с ядерным топливом, обычно окруженная отражателем нейтронов, теплоноситель, система регулирования цепной реакции, радиационная защита, система дистанционного управления. Основной характеристикой ядерного реактора является его мощность. Мощность в 1 МВт соответствует цепной реакции, в которой происходит 3·10¹⁶ актов деления в 1 сек.

Конструкция

Любой ядерный реактор состоит из следующих частей:

§ Активная зона с ядерным топливом и замедлителем;

§ Отражатель нейтронов, окружающий активную зону;

§ Теплоноситель;

§ Система регулирования цепной реакции, в том числе аварийная защита;

§ Радиационная защита;

§ Система дистанционного управления.

§

Производство энергии, являющееся необходимым средством для существования и развития человечества, оказывает воздействие на природу и окружающую человека среду. С одной стороны в быт и производственную деятельность человека настолько твердо вошла тепло- и электроэнергия, что человек даже и не мыслит своего существования без нее и потребляет само собой разумеющиеся неисчерпаемые ресурсы. С другой стороны, человек все больше и больше свое внимание заостряет на экономическом аспекте энергетики и требует экологически чистых энергетических производств. Это говорит о необходимости решения комплекса вопросов, среди которых перераспределение средств на покрытие нужд человечества, практическое использование в народном хозяйстве достижений, поиск и разработка новых альтернативных технологий для выработки тепло- и электроэнергии и т.д.

Современный период развития человечества иногда характеризуют через три «Э»: энергетика, экономика, экология. Энергетика в этом ряду занимает особое место. Она является определяющей и для экономики, и для экологии. От нее в решающей мере зависит экономический потенциал государств и благосостояние людей. Она же оказывает наиболее сильное воздействие на окружающую среду, экосистемы и биосферу в целом. Самые острые экологические проблемы (изменение климата, кислотные осадки, всеобщее загрязнение среды и другие) прямо или косвенно связаны с производством, либо с использованием энергии. Энергетике принадлежит первенство не только в химическом, но и в других видах загрязнения: тепловом, аэрозольном, электромагнитном, радиоактивном. Поэтому не будет преувеличением сказать, что от решения энергетических проблем зависит возможность решения основных экологических проблем. Энергетика - это та отрасль производства, которая развивается невиданно быстрыми темпами. Если численность населения в условиях современного демографического взрыва удваивается за 40-50 лет, то в производстве и потреблении энергии это происходит через каждые 12-15 лет. При таком соотношении темпов роста населения и энергетики, энерговооруженность лавинообразно увеличивается не только в суммарном выражении, но и в расчете на душу населения.

§ Нет основания ожидать, что темпы производства и потребления энергии в ближайшей перспективе существенно изменятся (некоторое замедление их в промышленно развитых странах компенсируется ростом энерговооруженности стран третьего мира), поэтому важно получить ответы на следующие вопросы:

§ - какое влияние на биосферу и отдельные ее элементы оказывают основные виды современной (тепловой, водной, атомной) энергетики и как будет изменяться соотношение этих видов в энергетическом балансе в ближайшей и отдаленной перспективе;

§ - можно ли уменьшить отрицательное воздействие на среду современных (традиционных) методов получения и использования энергии;

§ - каковы возможности производства энергии за счет альтернативных (нетрадиционных) ресурсов, таких как энергия солнца, ветра, термальных вод и других источников, которые относятся к неисчерпаемым и экологически чистым.

§ В настоящее время энергетические потребности обеспечиваются в основном за счет трех видов энергоресурсов: органического топлива, воды и атомного ядра. Энергия воды и атомная энергия используются человеком после превращения ее в электрическую

§ энергию. В то же время значительное количество энергии, заключенной в органическом топливе, используется в виде тепловой и только часть ее превращается в электрическую. Однако и в том и в другом случае высвобождение энергии из органического топлива связано с его сжиганием, а, следовательно, и с поступлением продуктов горения в окружающую среду. Познакомимся с основными экологическими последствиями современных способов получения и использования энергии.

Билет 10:

На всякий заряд, находящийся в электрическом поле, действует сила, и поэтому при движении заряда в поле совершается определенная работа. Эта работа зависит от напряженности поля в разных точках и от перемещения заряда. Но если заряд описывает замкнутую кривую, т. е. возвращается в исходное положение, то совершаемая при этом работа равна нулю, как бы ни было сложно поле и по какой бы прихотливой кривой ни происходило движение заряда.
Это важное свойство электрического поля нужно несколько пояснить. Для этого рассмотрим сначала движение тела в поле силы тяжести. Работа, как мы знаем (см. том I), равна произведению силы на перемещение и на косинус угла между ними: 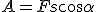. Если этот угол острый ( 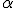<90°), то работа положительна, если же угол тупой ( 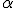>90°), то работа отрицательна. В первом случае мы получаем работу за счет действия силы 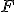, во втором — затрачиваем работу на преодоление этой силы. Представим себе, что в поле земного притяжения, т. е. в пространстве вблизи земной поверхности, где действует гравитационная сила притяжения к Земле, перемещается какое-нибудь. тело. Мы предполагаем, что при этом перемещении нет трения, так что тело не испытывает изменений состояния, которые могут сопровождаться изменениями его внутренней энергии: тело не нагревается, не распадается на части, не изменяет своего агрегатного состояния, не испытывает пластической деформации и т. д. В таком случае всякое перемещение тела в поле силы тяжести может сопровождаться лишь изменением потенциальной и кинетической энергии. Если тело опускается, то потенциальная энергия системы Земля — тело уменьшается, а кинетическая энергия тела соответственно увеличивается; наоборот, при подъеме тела происходит возрастание потенциальной энергии и одновременно уменьшение кинетической энергии. При этом полная механическая энергия, т. е. сумма потенциальной и кинетической, остается постоянной (см. том I) Как бы ни был сложен путь тела в поле силы тяжести (подъем и опускание по вертикальной, наклонной или криволинейной траектории, передвижение по горизонтальному направлению), но если в конце концов тело приходит в исходную точку, т. е. описывает замкнутый путь, то система Земля — тело возвращается в исходное положение и имеет ту же самую энергию, какой она обладала до начала перемещения тела. Это означает, что сумма положительных работ, совершенных силой тяжести при опускании тела, равна по модулю сумме отрицательных работ, совершенных силой тяжести на участках пути, соответствующих подъему тела. Поэтому алгебраическая сумма всех работ, совершаемых силой тяжести на отдельных участках пути, т. е. полная работа на замкнутом пути, равна нулю.
Из изложенного ясно, что наш вывод справедлив лишь в том случае, если в процессе участвовала лишь сила тяжести и отсутствовала сила трения и всевозможные другие силы, могущие вызвать указанные выше изменения внутренней энергии. Таким образом, силы гравитационного поля, в отличие от многих других сил, например сил трения, обладают свойством, которое мы можем сформулировать так: работа, совершаемая гравитационными силами при перемещении тела по замкнутому пути, равна нулю. Нетрудно видеть, что это свойство гравитационных сил является выражением закона сохранения (консервации) полной механической энергии. В связи с этим силовые поля, которые обладают указанным свойством, называют консервативными.

Подобно гравитационному полю, электрическое поле, создаваемое покоящимися электрическими зарядами, также является консервативным. Когда в нем перемещается заряд, то на тех участках пути, где направление перемещения составляет с направлением силы острый угол (например, в точке а на рис. 38), работа, совершаемая силами поля, положительна. Напротив, там, где направление перемещения составляет с направлением силы тупой угол (в точке b), работа сил электрического поля отрицательна.
Когда заряд, пройдя по замкнутому пути, вернется в исходную точку, полная работа электрических сил на этом пути, представляющая собой алгебраическую сумму положительных работ на одних участках и отрицательных на других, равна нулю.
Строгое математическое доказательство консервативности электрического поля в общем случае довольно сложно, и мы ограничимся поэтому доказательством этого свойства поля для простейшего случая — поля, создаваемого одним точечным зарядом.
Пусть в электрическом поле неподвижного точечного заряда 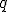другой заряду движется вдоль произвольной замкнутой кривой 1—2—3—4— 5—6—1 (рис. 38) и после обхода вдоль кривой возвращается в исходную точку 1. Для подсчета совершаемой при этом работы проведем мысленно ряд сфер с центром в заряде 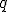, которые разобьют весь путь заряда 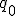на малые отрезки, и рассмотрим два отрезка 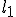и 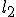, лежащие между одними и теми же сферами (между точками 2 и 3, 5 и 6). Если отрезк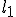и и 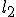достаточно малы, то можно считать, что сила, действующая на заряд 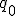, вo всех точках каждого из отрезков постоянна. Так как оба отрезка находятся на равных расстояниях от заряда 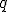, то, согласно закону Кулона, силы взаимодействия зарядов на обоих отрезках одинаковы по модулю, но отличаются направлением, образуя разные углы 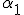и 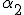с направлением перемещения. Наконец, при достаточной малост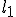и и 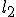эти отрезки можно считать прямолинейными. Поэтому работа 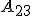, совершаемая электрическими силами на пути 2—3, будет равна произведению силы на перемещение и на косинус угла между направлениями силы и перемещения, т. е. что алгебраическая сумма работ на отрезках 2—3 и 5—6 равна нулю. Такой же результат мы получим и для любой другой пары соответствующих отрезков пути, заключенных между другими сферами. Поэтому и полная работа при обходе по замкнутому контуру, равная сумме работ на отдельных отрезках, тоже будет равна нулю.
Мы получили результат для случая электрического поля одного точечного заряда. Он оказывается справедливым для любого электростатического поля, т. е. поля, созданного неподвижными зарядами, так как поле, создаваемое любым распределением заряда, можно свести к полю совокупности точечных зарядов.
Итак, в электрическом поле работа при перемещении заряда по замкнутому контуру всегда равна нулю.
Так как работа на пути 1—2—3—4—5—6—1 равна нулю, то, следовательно, работа на пути 1—2—3—4 равна по модулю и противоположна по знаку работе на пути 4—5—6—1. Но работа при перемещении заряда на пути 4—5—6—1 равна по модулю и противоположна по знаку работе при перемещении того же заряда во встречном направлении, т. е. по пути 1—6—5—4. Отсюда следует, что работа на пути 1—2—3—4 (рис. 38) имеет тот же модуль и знак, что и работа на пути 1—6—5—4. Так как выбранный криволинейный контур совершенно произволен, то полученный результат можно выразить еще и так: работа, совершаемая электрическими силами при перемещении заряда между двумя точками в электрическом поле, не зависит от формы пути. Она определяется только положением начальной и конечной точек пути.

Разность потенциалов. Напряжение

Работа сил электростатического поля по перемещению заряда q₀ из точки 1 в точку 2 поля

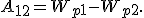
Выразим потенциальную энергию через потенциалы поля в соответствующих точках:

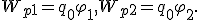
Тогда

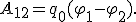
Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.

Из этой формулы разность потенциалов

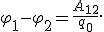
Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.

В СИ единицей разности потенциалов является вольт (В).

1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.

Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов φ₁ - φ₂ часто называют электрическим напряжением между данными точками поля:

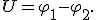
Напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.

Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах. 1 эВ равен работе, совершаемой силами поля при перемещении электрона (е = 1,6·10^-19 Кл) между двумя точками, напряжение между которыми равно 1 В.

1 эВ = 1,6·10^-19 Кл·1 В = 1,6·10^-19 Дж.

1 МэВ = 10⁶ эВ = 1,6·10^-13 Дж.

Электрическое поле графически можно изобразить не только с помощью линий напряженности, но и с помощью эквипотенциальных поверхностей.

Эквипотенциальной называется воображаемая поверхность, в каждой точке которой потенциал одинаков. Разность потенциалов между двумя любыми точками эквипотенциальной поверхности равна нулю.

Следовательно, работа по перемещению заряда вдоль эквипотенциальной поверхности равна 0. Но работа рассчитывается по формуле 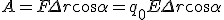. Здесь q₀ ≠ 0, Е ≠ 0, Δr ≠ 0. Значит, .

Следовательно, линии напряженности перпендикулярны эквипотенциальным поверхностям. Первая эквипотенциальная поверхность металлического проводника — это поверхность самого заряженного проводника, что легко проверить электрометром. Остальные эквипотенциальные поверхности проводятся так, чтобы разность потенциалов между двумя соседними поверхностями была постоянной.

Картины эквипотенциальных поверхностей некоторых заряженных тел приведены на рис. 3.

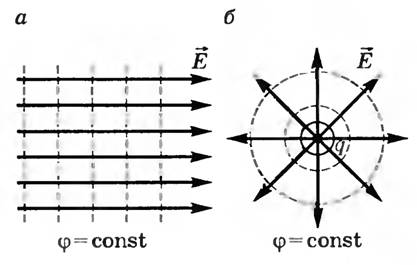
Рис. 3

Эквипотенциальными поверхностями однородного электростатического поля являются плоскости, перпендикулярные линиям напряженности (рис. 3, а).

Эквипотенциальные поверхности поля точечного заряда представляют собой сферы, в центре которых расположен заряд q (рис. 3, б).

Билет 11:

В 1820 г. датский физик Эрстед обнаружил магнитное действие тока. Это явление заключается в том, что магнитная стрелка, помещенная вблизи проводника с током, отклоняется от плоскости магнитного меридиана и уже, как правило, не указывает с севера на юг.
Над неподвижным проводом 1, расположенным вдоль меридиана, т. е. в направлении север — юг, подвешена на тонкой нити магнитная стрелка 2. Стрелка, как известно, устанавливается также приблизительно по линии север — юг, и поэтому она располагается примерно параллельно проводу. Но как только мы замкнем ключ и пустим ток по проводу 1, мы увидим, что магнитная стрелка поворачивается, стремясь установиться под прямым углом к нему, т. е. в плоскости, перпендикулярной к проводу. Этот фундаментальный опыт показывает, что в пространстве, окружающем проводник с током, действуют силы, вызывающие движение магнитной стрелки, т. е. силы, подобные тем, которые действуют вблизи естественных и искусственных магнитов. Такие силы называют магнитными силами, так же, как силы, действующие на электрические заряды, называют электрическими.
Для изучения конфигурации магнитного поля, создаваемого током, можно использовать способ железных опилок. Если через отверстие в картонной пластинке пропустить прямолинейный проводник достаточной длины и затем насыпать на картон железные опилки и пропустить по проводнику электрический ток, то опилки расположатся в виде концентрических окружностей с центром на оси проводника. Силовые линии магнитного поля прямолинейного тока лежат в плоскости, перпендикулярной току, и представляют собой концентрические окружности с центром на оси тока.
Для определения направления силовых линий можно воспользоваться небольшими магнитными стрелками. Расположение силовых линий магнитного поля прямолинейного тока дает возможность установить правило, по которому всегда легко опред<