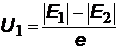Распределение энергии в спектре АЧТ.
Распределение энергии в спектре АЧТ.
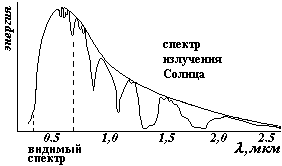
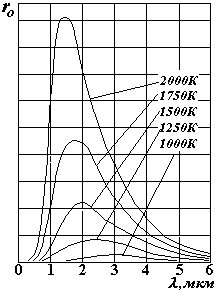 На рисунке приведена зависимость излучательной способности АЧТ от длины волны при различных температурах. Эти данные получены экспериментально. Из графиков видно, что энергия распределяется по длинам волн неравномерно, с увеличением температуры излучение резко возрастает. При указанных температурах максимумы излучения попадают в инфракрасный диапазон длин волн, на видимую область (0,4-0,75 мкм) приходится незначительное количество энергии . С ростом температуры максимумы смещаются в сторону более коротких длин волн. На втором рисунке приведен для сравнения спектр солнечного излучения. «Провалы» в спектре – это линии поглощения атмосферой, огибающая – спектр излучения АЧТ.
На рисунке приведена зависимость излучательной способности АЧТ от длины волны при различных температурах. Эти данные получены экспериментально. Из графиков видно, что энергия распределяется по длинам волн неравномерно, с увеличением температуры излучение резко возрастает. При указанных температурах максимумы излучения попадают в инфракрасный диапазон длин волн, на видимую область (0,4-0,75 мкм) приходится незначительное количество энергии . С ростом температуры максимумы смещаются в сторону более коротких длин волн. На втором рисунке приведен для сравнения спектр солнечного излучения. «Провалы» в спектре – это линии поглощения атмосферой, огибающая – спектр излучения АЧТ.
Законы изучения АЧТ. На основании экспериментальных данных были получены следующие законы:
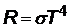 | Закон Стефана-Больцмана «Энергетическая светимость АЧТ прямо пропорциональна четвертой степени абсолютной температуры». Из закона следует, что при небольшом увеличении температуры, энергия излучения возрастает очень сильно. Например, при увеличении температуры в 2 раза, излучаемая энергия возрастает в 16 раз. s = 5,67×10-8 Вт/(м2К4) – постоянная Стефана-Больцмана. |
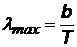 | Закон смещения Вина: «Длина волны, на которую приходится максимум излучения, обратно пропорциональна абсолютной температуре». Из закона следует, что с увеличением температуры максимум излучения смещается в сторону более коротких волн. b= 2,9×10-3 1/м – постоянная Вина. |
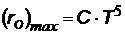 | Закон общепринятого названия не имеет, иногда называется 2-ым законом Вина: «Максимальная излучательная способность прямо пропорциональна пятой степени абсолютной температуры» С = 1,3×10-5 Вт/(м3.К5)- коэффициент пропорциональности |
Выясним, что представляют собой величины в формулах (§) и (§§) на графике зависимости излучательной способности АЧТ ro от длины волны l.
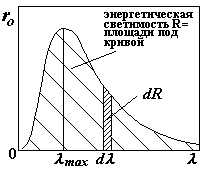 | Кривая излучения АЧТ. dR – поток излучения, приходящийся на интервал длин волн dl (площадь плотно заштрихованной полоски) R – интеграл (см. формулу §§) – на графике – это площадь под всей кривой излучения. lmax – длина волны, на которую приходится максимум излучения |
Гипотеза и формула Планка.
Все попытки получить формулу, описывающую кривую излучения АЧТ оказались безуспешными. Две из полученных формул (формула Вина и формула Релея и Джинса) достаточно хорошо подходили при малых и при больших длинах волн, но полностью описать кривую не могли (см. таблицу ниже). Получить формулу, полностью описывающую кривую излучения АЧТ удалось Планку. Он впервые выдвинул квантовую гипотезу(1900 г)о том, что свет испускается порциями – квантами. Энергия одного кванта пропорциональна частоте излучения. Это была принципиально новая гипотеза, положившая начало развитию квантовой теории.
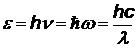 | энергия кванта (фотона), выраженная через частоту n (Гц), циклическую частоту w (1/с)и длину волны l |
h = 6,625×10-34 Дж.с - постоянная Планка 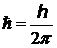 = 1,05×10-34 Дж.с = 1,05×10-34 Дж.с 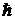 - называют квантом действия (в устной речи произносится «аш перечеркнутая - называют квантом действия (в устной речи произносится «аш перечеркнутая |
Мы не будем приводить вывод формулы Планка , укажем только, что он основан на методах статистической термодинамики, как и вывод формул Вина и Релея-Джинса, но Планк предположил, что энергия, приходящаяся на одну степень свободы колебательного движения осциллятора равна не кТ/2, а зависит от частоты излучения.
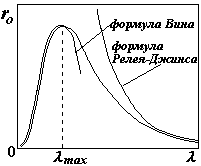 Приближенная формула Вина хорошо выполняется при малых длинах волн (см. рис.) и дает максимум; формула Релея - Джинса дает неплохое совпадение с опытом при больших длинах волн, но кривая уходит в бесконечность, что физически невозможно. (Подробнее – см. таблицу ниже)
Приближенная формула Вина хорошо выполняется при малых длинах волн (см. рис.) и дает максимум; формула Релея - Джинса дает неплохое совпадение с опытом при больших длинах волн, но кривая уходит в бесконечность, что физически невозможно. (Подробнее – см. таблицу ниже)
| Название | выражение через частоту n | выражение через длину волны l |
| формула Планка | 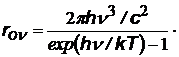 ª ª | 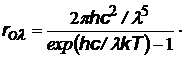 ªª ªª |
| формула Вина, хорошо выполняется при hn>> kT или l£ lmax = b/T b = 0,0029 м.К (см.ранее закон смещения Вина | 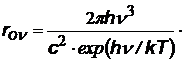 | 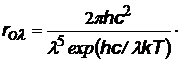 |
| формула Релея - Джинса хорошо выполняется при hn << kT или l >> l max = b/T (ех » 1+ х при малых х) | 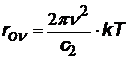 | 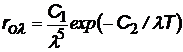 С1 » 3,7×10-16 Вт.м2 С2»1,4×10-2 м.К С1 » 3,7×10-16 Вт.м2 С2»1,4×10-2 м.К |
Из формулы Планка можно получить теоретически все законы излучения АЧТ.
| Чтобы получить закон Стефана-Больцмана, нужно просуммировать излучение по всем частотам | Подставим под интеграл (ª), сделаем замену переменной. Интеграл получается не табличный, но известен из математики; А = const, в которой собраны все постоянные, входящие в формулу Планка |
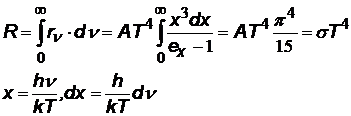 | |
| Чтобы получить закон смещения Вина, нужно приравнять первую производную излучательной способности нулю, что будет соответствовать максимуму излучения drol / dl = 0. Возьмем формулу (ªª), найдем производную, получим уравнение. Введем переменную x =hc / kTl подставим в уравнение | В результате получим: 5(ex – 1) -xex = 0 Это уравнение можно решить только численно: х» 5. Подставляя, найдем: l = const/T |
Законы теплового излучения используются в приборах, с помощью которых измеряют бесконтактным способом температуру тел, нагретых до высоких температур. Такие приборы называются пирометрами. Шкала такого прибора заранее проградуирована. С помощью оптических линз изображение источника излучения (например, отверстия печи, лампочки накаливания) фокусируется на датчике прибора, и стрелка указывает температуру на шкале прибора.
ДУАЛИЗМ СВОЙСТВ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ
Прежде, чем перейти к закономерностям фотоэффекта и эффекта Комптона, рассмотрим свойства света (электромагнитного излучения). В одних явлениях (интерференция, дифракция, поляризация) свет проявляется себя как волны, в других (тепловое излучение, фотоэффект, эффект Комптона) – как частицы (кванты, фотоны), поэтому говорят о двойственной, корпускулярно волновой природе света. Если частота света и, следовательно, энергия фотона, велика, то свет проявляется себя как «частицы», при малых частотах – как волны. Например, в области радиоволн квантовые свойства практически не проявляются, и волновая электромагнитная теория хорошо объясняет явления, связанные с радиоволнами.
В силу двойственности природы света, для его характеристики используются как квантовые, так и волновые величины.
Свет как фотоны (кванты) характеризуется:
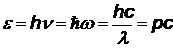 | энергия фотона |
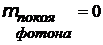 | масса покоя фотона равна 0. Действительно, энергия частицы по формуле Эйнштейна 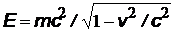 , скорость света (и фотона) в вакууме равна с, следовательно, m = 0 , скорость света (и фотона) в вакууме равна с, следовательно, m = 0 |
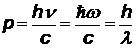 | импульс фотона. Действительно, из СТО энергия частицы связана с ее импульсом 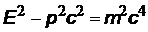 ,m=0 Þ hn = pc ,m=0 Þ hn = pc |
Свет как электромагнитные волны характеризуются:
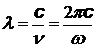 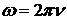 | l- длина волны, n - частота (в Гц), w - циклическая частота, с – скорость света в вакууме |
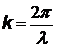 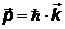 | k в скалярной форме называют волновым числом, в векторной форме называют волновым вектором р – импульс фотона |
| В атомной физике энергию обычно измеряют не в джоулях, а в электронвольтах (эВ). 1 эВ = 1,6×10-19 Дж. Электронвольт численно равен той энергии, которую приобретает электрон, пройдя разность потенциалов в 1 вольт. Электронвольты и вольты численно совпадают, хотя этими единицами измеряются совершенно разные величины. Например, электрон пройдя разность потенциалов 5 В приобретает энергию 5 эВ. |
В нашем мире мы не наблюдаем таких макрообъектов, которые проявляли бы себя то как частицы, то как волны. Поэтому все попытки представить себе, что же такое свет, оказались безуспешными. Фотоны не подчиняются законам классической механики. Двусмысленность природы света возникает потому, что мы используем классические представления для описания неклассических, квантовых объектов.
ФОТОЭФФЕКТ
Фотоэффектом называют электрические явления, происходящие под действием электромагнитного излучения (света). Различают следующие виды фотоэффекта.
1)Внешний фотоэффект. Он состоит в том, что под действием света происходит
испускание электронов из вещества (см. рис.). При этом на поверхности
вещества появляется положительный заряд.
2)Внутренний фотоэффект. Выбитые светом электроны остаются в веществе.
Если к веществу приложена разность потенциалов, то при освещении светом
электропроводность вещества увеличивается.
3)Фотоэффект в запирающем слое (вентильный фотоэффект). Если привести в контакт два вещества с разным типом проводимости (электронной и дырочной), то на их границе возникает разность потенциалов. Если освещать границу контакта светом и цепь замкнуть, то в ней будет протекать ток. Таким образом, можно наблюдать непосредственное преобразование световой энергии в электрическую (подробнее см.дальше - ФТТ)
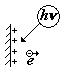 внешний фотоэффект внешний фотоэффект | 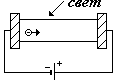 внутренний фотоэффект внутренний фотоэффект | 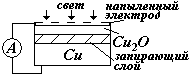 фотоэффект в запирающем слое фотоэффект в запирающем слое |
Мы будем рассматривать только внешний фотоэффект. Попытки объяснить закономерности фотоэффекта на основе электромагнитной теории оказались невозможными, например, из теории следовало, что появление фототока должно происходить спустя десятки минут после освещения, тогда как из опыта фототок появлялся практически мгновенно. В 1905 г Эйнштейн показал, что закономерности внешнего фотоэффекта можно объяснить, если предположить, что свет поглощается порциями (квантами) такими же, как по предположению Планка свет излучается. Он предложил уравнение:
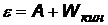 © © | уравнение Эйнштейна для внешнего фотоэффекта |
По сути – это закон сохранения энергии: энергия фотона e расходуется на работу А по отрыву электрона от атома и на сообщение электрону кинетической энергии Wкин . (На свободном, не связанном с атомом электроне, фотоэффект невозможен).
Фотоэффект можно рассматривать как неупругое столкновение частицы-фотона с атомом; фотон исчезает, из атома вылетает электрон, и часть импульса «погибшего» фотона передается атому.
Для удобства решения задач соберем все выражения для величин в формуле
(©) в таблицу. В зависимости от условия задачи, следует выбрать подходящие
формулы и подставить в (©).
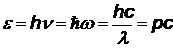 | энергия падающего фотона | ||
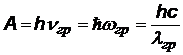 | А – работа выхода электрона из вещества | ||
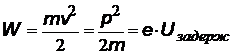 | максимальная кинетическая энергия электрона. Uзадерж- задерживающий потенциал (см.дальше), е – заряд электрона, р – импульс электрона | ||
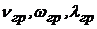 | все эти величины называются красной границей фотоэффекта. Красная граница фотоэффекта – это частота или длина волны, при которых начинается (или прекращается) фотоэффект | 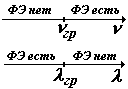 | |
| W, v, p | Кинетическая энергия, скорость и импульс в формуле Эйнштейна являются максимальными, т.е. электрон имеет их сразу же после отрыва от атома. «Пробираясь к выходу» из вещества за счет взаимодействия с другими частицами, он может потерять энергию, поэтому вылетевшие электроны имеют различные скорости (вплоть до 0). | ||
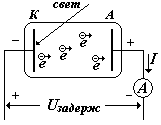
| Uзадерж | задерживающее напряжение (потенциал) – это обратное напряжение, которое нужно приложить между катодом и анодом фотоэлемента, чтобы прекратился фототок (см. рис. ниже) | ||
 Рассмотрим вакуумный фотоэлементи его характеристики.1)Вольтамперная характеристика.
Рассмотрим вакуумный фотоэлементи его характеристики.1)Вольтамперная характеристика.
На рисунке показана схема, используемая для изучения фотоэффекта. Внутри стеклянного баллона, из которого откачен воздух, имеются два электрода: катод (К) и анод (А). Такое устройство называется вакуумным фотоэлементом. При освещении катода светом, из него будут вылетать электроны, образуя электронное облако. Часть электронов по инерции достигнут анода. Если катод и анод замкнуть вне баллона и подсоединить микроамперметр, то прибор покажет ток.
Этот очень небольшой ток называется инерционным (Iин).
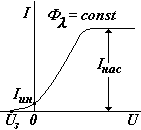 Если к электродам подсоединить батарею и увеличивать напряжение между катодом и анодом, ток в цепи будет увеличиваться. Зависимость фототока от напряжения называется вольтамперной характеристикой фотоэлемента ( см. рис.). Начиная с некоторых напряжений, ток перестает увеличиваться, если при этом световой поток
Если к электродам подсоединить батарею и увеличивать напряжение между катодом и анодом, ток в цепи будет увеличиваться. Зависимость фототока от напряжения называется вольтамперной характеристикой фотоэлемента ( см. рис.). Начиная с некоторых напряжений, ток перестает увеличиваться, если при этом световой поток
Ф остается постоянным. Максимальный ток называется током насыщения (Iнас). Существование тока насыщения объясняется следующим образом. Один фотон выбивает только один электрон, но не каждый фотон выбивает по электрону. Отношение числа выбитых электронов Nэл к числу падающих фотонов Nфот в единицу времени называется квантовым выходом. Квантовый выход a зависит от природы вещества и частоты фотонов.
Световая характеристика.
Световой характеристикой фотоэлемента называется зависимость фототока насыщения от падающего светового потока ( см.рис.). Квантовый подход приводит к прямой пропорциональности тока насыщения световому потоку
Iнасыщ ~ Ф. Действительно:
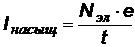 | ток насыщения, е – заряд электрона, t- время. | 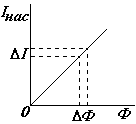 |
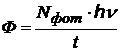 | световой поток | |
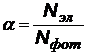 | квантовый выход | |
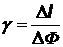 А/Вт А/Вт | чувствительность фотоэлемента | Iнасыщ = g Ф |
Отсюда для n = const следует, что сила тока насыщения прямо пропорциональна световому потоку. Коэффициент пропорциональности g называется чувствительностью фотоэлемента – она показывает, на сколько изменяется сила тока насыщения при изменении светового потока на единицу
Задерживающий потенциал.
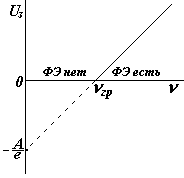 Уравнение Эйнштейна можно записать в виде:
Уравнение Эйнштейна можно записать в виде: 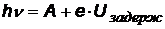 и выразить задерживающий потенциал:
и выразить задерживающий потенциал:
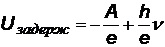 |
На рисунке показан график зависимости задерживающего потенциала от частоты падающего света. По графику можно найти работу выхода А, красную границу nгр , а по наклону прямой можно определить величину постоянной Планка h.
Фотоэлементы широко используются в физике и технике. Вакуумные фотоэлементы довольно громоздки и дают небольшие токи, но вследствие своей безинерционности и линейной световой характеристики они незаменимы в тех случаях, когда необходимо превратить световые сигналы в электрические без каких-либо искажений. Существование тока насыщения в фотоэлементах позволят использовать их в стабилизаторах (напряжение изменяется, а ток остается постоянным). Фотоэлементы очень часто применяют в турникетах, для подсчета движущихся изделий на конвейерах и т.п.
ЭФФЕКТ КОМПТОНА
Эффектом Комптона называется рассеяние веществом электромагнитного излучения, при котором частота рассеянного излучения уменьшается по сравнению с первоначальной, и одновременно наблюдается вылет быстрых электронов (электроны отдачи). Изменение частоты оказывается различной в зависимости от угла наблюдения. Американский ученый Комптон, открывший это явление (1923 г) разработал теорию явления. Он предложил рассматривать наблюдаемое взаимодействие света с веществом как упругое столкновение
частиц - фотона и электрона. Используя законы сохранения импульса и энергии, Комптон получил формулу для изменения длины волны в зависимости от угла рассеяния..
Мы не будем приводить полный вывод формулы для изменения длины волны, а запишем только законы сохранения и окончательную формулу. Так как эффект Комптона наблюдается только для фотонов с большой энергией (рентгеновские и гамма-лучи), то при вычислениях необходимо использовать формулы СТО, и вывод становится громоздким.
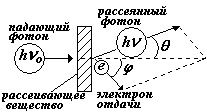 На рис. показано столкновение первоначального фотона с энергией hnо с электроном в веществе (на рис. не показан). Импульс и энергия электрона до столкновения пренебрежимо малы по сравнению с импульсом и энергией фотона, т.е. электрон можно считать свободным. (Обычно употребляется выражение «рассеяние фотона на свободном электроне»). После столкновения фотон отклоняется от первоначального направления под углом q , а его энергия уменьшается и становится равной hn.Электрон получает импульс и кинетическую энергию и летит под углом j. (электрон отдачи, угол отдачи).
На рис. показано столкновение первоначального фотона с энергией hnо с электроном в веществе (на рис. не показан). Импульс и энергия электрона до столкновения пренебрежимо малы по сравнению с импульсом и энергией фотона, т.е. электрон можно считать свободным. (Обычно употребляется выражение «рассеяние фотона на свободном электроне»). После столкновения фотон отклоняется от первоначального направления под углом q , а его энергия уменьшается и становится равной hn.Электрон получает импульс и кинетическую энергию и летит под углом j. (электрон отдачи, угол отдачи).
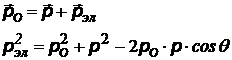 | закон сохранения импульса в векторном и скалярном виде (теорема косинусов). 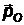 - импульс падающего фотона, - импульс падающего фотона, 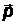 - импульс рассеянного фотона, - импульс рассеянного фотона, 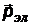 - импульс электрона. q - угол рассеяния - импульс электрона. q - угол рассеяния |
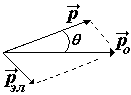 | |
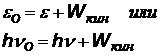 | закон сохранения энергии 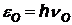 - энергия падающего фотона, - энергия падающего фотона, 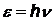 - энергия рассеянного фотона, - энергия рассеянного фотона, 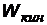 - кинетическая энергия электрона отдачи (электрон релятивистский). - кинетическая энергия электрона отдачи (электрон релятивистский). |
Подставив в эти законы выражения для указанных величин, приведенные ниже, после преобразований получим:
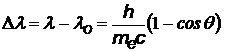 ¨ или ¨ или 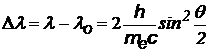 | изменение длины волны при комптоновском рассеянии излучения (на свободном электроне) Из формул следует, что комптоновское изменение длины волны не зависит от природы рассеивающего вещества, а определяется только углом наблюдения. |
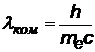 = 2,43 пм = 2,43×10-12 м = 2,43 пм = 2,43×10-12 м | Эта величина называется комптоновской длиной волны электрона |
Комптоновское рассеяние может наблюдаться и на свободном протоне, тогда следует использовать комптоновскую длину волны протона: 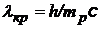
Из формулы (¨) следует, что изменение l при различных углах рассеяния равно:
| q = 0о | Dl = 0 | фотоны, продолжающие лететь в первоначальном направлении, не изменяют свою длину волны |
| q = 90о | Dl = 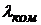 | в этом случае изменение l равно комптоновской длине волны электрона |
| q = 180о | Dl = 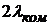 | максимальное изменение l происходит в случае, когда рассеянный фотон движется в противоположном направлении |
Ниже приводится таблица формул, используя которые можно получить выражение (¨) для Dl. Компактное расположение формул облегчает также решение задач.
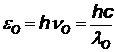 | 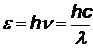 | энергия падающего и рассеянного фотонов |
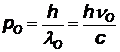 | 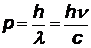 | импульс --²-- |
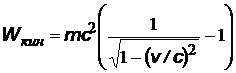 | релятивистская кинетическая энергия электрона отдачи | |
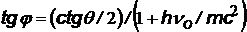 | по этой формуле можно найти угол отдачи j |
Комптоновское рассеяние наблюдается только для рентгеновских и гамма-лучей. В этом случае изменение длины волны сравнимо с длиной волны падающего излучения, и может быть измерено экспериментально. Для видимого света обнаружить эффект Комптона невозможно, т.к. максимальное изменение Dl = 0,48 пм слишком мало по сравнению со средней длиной световой волны
l » 500 нм = 500000 пм (зеленый свет) и перекрывается тепловым уширением спектральных линий..
Эффект Комптона доказывает, что: 1) свет имеет квантовую природу и
2) для элементарных процессов взаимодействия частиц применимы законы сохранения импульса и энергии.
ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ АТОМОВ И МОДЕЛЬ АТОМА БОРА.
Ядерная модель атома.
Резерфорд на основании опытов по рассеянию альфа-частиц на металлической фольге (1909-10 гг.) предложил ядерную (планетарную) модель атома. Атом представляет собой очень маленькое ядро, в котором сосредоточена почти вся масса атома, а вокруг ядра вращаются электроны подобно планетам солнечной системы. Эта модель оказалась несостоятельной, она не могла объяснить, почему спектры излучения газов состоят из отдельных линий, а не являются сплошными. Электроны, обладающие ускорением, должны непрерывно излучать электромагнитные волны, терять энергию и, в конце концов, упасть на ядро. Однако атомы являются устойчивыми системами.
В 1913 г Бор дополнил модель Резерфорда, выдвинув принципиально новые предположения (постулаты).
Постулаты Бора:
| В атомах существуют особые стационарные орбиты, на которых электрон может двигаться сколь угодно долго. | Целые числа 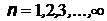 - номера орбит - получили впоследствии название квантовых чисел. При n = 1 - номера орбит - получили впоследствии название квантовых чисел. При n = 1 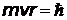 . Т.о. . Т.о. 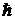 представляет собой минимальный момент импульса или минимальный квант действия представляет собой минимальный момент импульса или минимальный квант действия | |
Момент количества движения (момент импульса) электрона на таких орбитах равен: 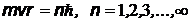 | ||
При переходе электрона с одной стационарной орбиты на другую происходит излучение (или поглощение) кванта энергии. 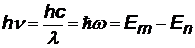 Е – энергия электрона на орбите Е – энергия электрона на орбите | 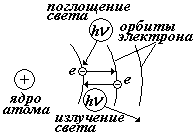 |
Теория Бора может быть названа полуклассической, полуквантовой. В этой теории движение электрона на орбите описывалось классическими законами (формулы – см. дальше). Вместе с тем, теория приводила к тому, что скорость, радиус орбиты, энергия электрона не могут иметь любые значения, а квантуются, т.е. могут принимать только дискретные (отдельные) значения.
Теория Бора хорошо описывала закономерности в спектре атома водорода и водородоподобных атомов.(Водородоподобными атомами называют атомы (или ионы) у которых на последней орбите имеется только один электрон). Однако, для атома гелия (Z = 2) и других элементов теория Бора не давала совпадения с опытом.
Атом водорода и водородоподобные атомы (ВПА) по теории Бора.
На рис. показан водородоподобный атом. Заряд ядра равен +Ze, где Z число протонов (и номер элемента в таблице Менделеева). Вокруг ядра вращается по круговой орбите электрон е со скоростью v. На электрон действует со стороны ядра кулоновская сила Fкул. Запишем II закон Ньютона для электрона: man=Fкул., где an = v2/ r - нормальное ускорение. (Взаимодействие электрона с другими электронами атома не учитываем).
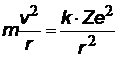 z z | II закон Ньютона и закон Кулона, к=1/4peо – коэффициент в СИ | 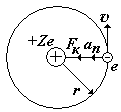 | Для атома водорода Z = 1 |
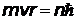 y y | постулат Бора |
Из этих формул получим выражения для скорости v и радиуса r орбиты электрона. Сократим в уравнении (z) на r, а оставшующуюся r перенесем в числитель левой части уравнения. Затем разделим уравнение (z) на (y) и получим v. Подставим v в (y) и найдем r.
Внимание! Легче запомнить вывод формул для v и r, чем сами формулы для них.
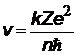 | скорость электрона на орбите, квантуется как v ~ 1/n; v1 = 2,2×106 м/с |
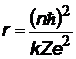 | радиус орбиты электрона, квантуется как r ~ n2 r1 = 0,53 нм – первый боровский радиус |
Когда электрон в атоме Н находится на 1-ой орбите, говорят, что электрон (или атом) находится в основном (невозбужденном) состоянии, при этом электрон имеет минимальную энергию. Все остальные состояния называются возбужденными состояниями.
Полная энергия Е электрона складывается из кинетической W и потенциальной U энергий: Е = W + U. Выразим их в идентичной форме:
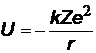 | Потенциальная энергия взаимодействия электрона с ядром отрицательна, т.к. нулевой уровень принят на бесконечности (U¥ = 0), чем ближе к ядру, тем меньше энергия электрона. | |
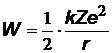 | Кинетическая энергия, получается из (z), т.к. W=mv2/2 | |
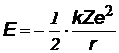 | Полная энергия: Е = W + U Подставив выражение для r, получим формулу: | |
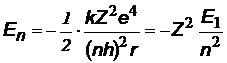 x x | Полная энергия электрона на n-ой орбите, квантуется как Е ~ 1/n2; вычисления дают: | |
| Е1 @ - 13,6 эВ Е1ВПА @ - Z 2 ×13,6 эВ | Энергия электрона на 1-ой орбите в атоме водорода и водородоподобных атомах (ВПА). | |
Из формулы (x) можно получить также:
|
Внимание!Не забывайте, что электронвольты и вольты численно равны.
Если подставить во 2-й постулат Бора 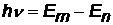 выражение (x), получим:
выражение (x), получим:
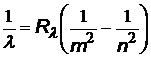 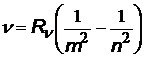 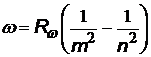 | все три формулы имеют одно и то же название – сериальные формулы, а константы называются постоянными Ридберга, хотя и имеют различные числовые значения |
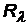 = 1,097×107 1/м = 1,097×107 1/м 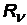 = 3,29×1015 1/с = 3,29×1015 1/с 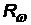 = 2,067×1016 1/с = 2,067×1016 1/с | 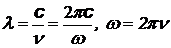 с помощью этих формул можно выразить одну постоянную через другую с помощью этих формул можно выразить одну постоянную через другую |
Сериальная формула была известна из опыта до появления теории Бора.
Закономерности в видимом спектре атома Н были обнаружены Бальмером еще в 1885 г. Затем были открыты другие серии. Они получили следующие названия:
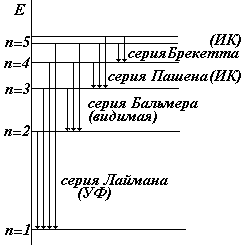 | серия Лаймана | 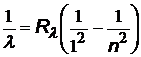 | n = 2, 3, 4,… |
| серия Бальмера | 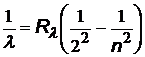 | n = 3, 4, 5,… | |
| серия Пашена | 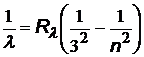 | n = 4, 5, 6,… | |
| серия Брекетта | 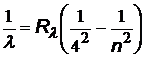 | n = 5, 6, 7,… |
Головными линиями серий называют: серия Лаймана переход 2®1, серия Бальмера переход 3®2, серия Пашена переход 4®3.
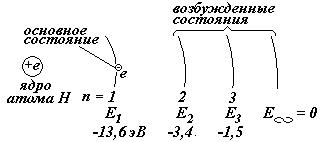 Чтобы электрон перешел на более удаленную орбиту, необходимо внешнее воздействие. Например, можно газ нагревать, или освещать светом, или к электродам в баллоне с газом приложить разность потенциалов. Среднее время жизни электрона на этой орбите порядка 10-8 секунды.
Чтобы электрон перешел на более удаленную орбиту, необходимо внешнее воздействие. Например, можно газ нагревать, или освещать светом, или к электродам в баллоне с газом приложить разность потенциалов. Среднее время жизни электрона на этой орбите порядка 10-8 секунды.
ПРИНЦИПЫ КВАНТОВОЙ МЕХАНИКИ. УРАВНЕНИЕ ШРЁДИНГЕРА.
Уравнение Шрёдингера.
Открытие двойственной природы частиц привело к пониманию о невозможности описывать поведение микрочастиц с помощью классических представлений и законов. Стало ясно, что нельзя говорить о траектории частицы, т.е. о точном ее местоположении в любой момент времени. Появилась новая наука – квантовая механика. Вместо слова траектория частицы было введено понятие о вероятности нахождения частицы в том или ином месте пространства. Для описания поведения микрочастиц Шрёдингер (1926 г) предложил дифференциальное уравнение:
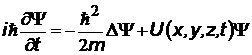 i i | нестационарное уравнение Шрёдингера; решение уравнения позволяет найти вероятность нахождения частицы в том или ином мете пространства | |
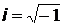 | мнимая единица | |
| m | масса рассматриваемой частицы | |
| U(x,y,z,t) | потенциальная энергия частицы, зависящая в общем случае от координат и времени | |
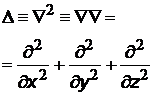 | оператор Лапласа (или лапласиан) краткое обозначение математической операции дифференцирования в частных производных; 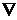 - набла (греч. слово nabla - арфа, символ по форме напоминает этот инструмент) - набла (греч. слово nabla - арфа, символ по форме напоминает этот инструмент) | |
| Y(x,y,z,t) | пси-функция или волновая функция, физического смысла не имеет, но квадрат ее модуля êYê2 – это вероятность нахождения частицы в данном месте пространства (подробнее см. дальше – стационарное уравнение Шрёдингера) | |
Математически уравнение Шрёдингера имеет бесконечное число решений, что физически неприемлемо, поэтому на пси-функцию накладываются дополнительные условия:
1).Пси-функция должна быть:
а) конечной – вероятность не может быть больше 1,
б) непрерывной – вероятность не может внезапно оборваться,
в) однозначной – не может быть две вероятности в одной точке,
2) Производные пси-функции должны быть непрерывны,
3) Пси-функция должна подчиняться условию нормировки:
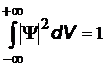 | условие нормировки; смысл его в том, что вероятность обнаружить частицу во всем мыслимом пространстве равна 1. |
В тех случаях, когда потенциальная энергия зависит только от координат и не зависит от времени, т.е U = U (x,y,z), пси-функцию можно представить как произведение двух функций: Y(x,y,z,t) = y ( x,y,z)×j (t). (Y - большая буква пси,
y - малая буква пси, обе функции называются пси- или волновыми функциями.) Подставим в уравнение (i) и, разделим на (y×j).. Получим:
 | Левая часть уравнения зависит только от t, правая – только от координат, следовательно, каждая из них должна быть равна некоторой постоянной, которую мы обозначим Е. | |||
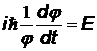 | 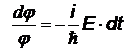 | 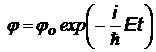 | j(t) называется временнОй частью пси-функции, со временем она затухает | |
Если приравнять константе Е правую часть уравнения, получим:
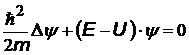 a a | стационарное уравнение Шрёдингера Е – полная энергия частицы, U – потенциальная энергия |
При решении уравнения Шредингера мы
| задаем | находим |
| U – потенциальную энергию частицы m – массу частицы | y - пси-функцию (собственные функции) Е – полную энергию частицы (собственные значения) |
Решение уравнения с учетом дополнительных условий, накладываемых на пси-функцию, приводит не к любым величинам энергии Е, а к дискретным:
Е1, Е2,…, Еn . В теории Бора электрон мог находиться тоже только в дискретных энергетических состояниях, но при этом была введена искусственно гипотеза о квантовании момента импульса электрона. Уравнение Шрёдингера приводит к квантованию энергии естественно, как математическое решение.
При решении оказывается, что данному энергетическому состоянию частицы могут соответствовать одна или несколько (к) пси-функций. Иначе говоря, при данной энергии Еn частица может вести себя по-разному. Тогда говорят, что уровень Еn к-кратно вырожден и обозначают пси-функцию как 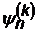 Если на систему воздействовать внешним, например магнитным полем, то вырождение снимается, уровень расщепляется на несколько уровней. Практически это обнаруживается в спектрах, вместо одной линии появляются несколько. Например, в спектре атома водорода на приборе с большим разрешением можно обнаружить, что почти все линии спектра являются дублетами.
Если на систему воздействовать внешним, например магнитным полем, то вырождение снимается, уровень расщепляется на несколько уровней. Практически это обнаруживается в спектрах, вместо одной линии появляются несколько. Например, в спектре атома водорода на приборе с большим разрешением можно обнаружить, что почти все линии спектра являются дублетами.
Рассмотрим подробнее пси-функцию.
| y - пси-функция | физического смысла не имеет |