Кинематическая энергия вращательного движения

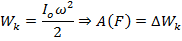
Для системы материальных точек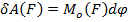

Где 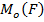суммарный момент внешних сил проекции на оси вращении: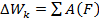

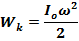
Где I_o момент инерции системы отосително той же непрдвижно ось

15) Плоское движение твердого тела на примере качения тела без проскальзывания.

Плоское движение твердого тела называется такое движение при котором связи точек тела движутся параллельно плоскотях.

Примеры плоского движения: качение колеса.

С – центр колеса

А – касательная точка с полем

В – высше колеса

1) Элементально перемещение любой точки кодеса приводят кочение без показываний, является поворот точку колеса на малой угол относительно оси проходяющий точки А.

Точка А - точка касательная общая померно. Все остальные точки провозуют данны времени от оси А одиноковый угловой скорость и угловой ускорение.

Ось А: называется макловенная ось вращения

Тогда:

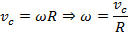
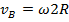
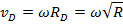
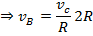
Тогда кинетическая энергия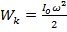

I_o момент инерции системы отосително точки А

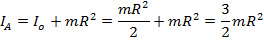
В этом случае:

1) Динамическое движение уравнения

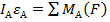
2) Сложное движение колеса (качение без прокатывания) можно рассмотрить как сумма двух движений:

a. Поступательное движение, скорость равна скорости центра масс

b. Вращателное всех точек колеса относително оси проходяющих через цетр масс стопкой угловой, чтобы скорость общая была равна движении уентр масс. Реально было

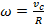
Тогда :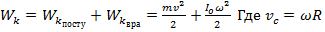

При этом динамика описывает двух уравнения

+) 2_ой Закон Ньютона для центра масс

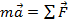
+) основные уравнение динамического вращателного движения

+)

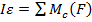
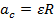
16)Механические колебания.Гармонические колебания.Дефференциальное уравнение гармонических колебаний.Динамика и механическая энергия гармонических колебаний.

Колебательное движение: такое движение, для которого характерно определение повторяемость физических величин, характер это движение.

Колебание называется периодическими, если эта повторяемось значения физических величин происходит через одиннокавый промежутки времени.

Мимимальный интервал времени, через которой повторяется физические велиины, характуризующие колебательный процесс называется периодом.

Механического колебания – колебание, при которых повторяются значения механических величин (координата, скорость, ускорение).

Колебание называется гармоническими, если характерные физическиого величины изменяются по гармоническим законым.

.

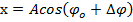Смещение — это отклонение от положения равнове­сия

А : Амплитуда колебаний – макисальной смещение проекции точки вдоль оси Х

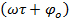: фаза колебаний

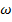: называется циклической частотой колебания

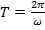: период колебаний(время одного польного колебания)

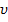: частота (число колебакии за 1с)

Пусть .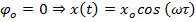

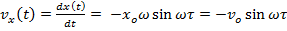Где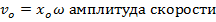

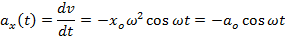
Рассмотрим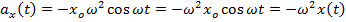

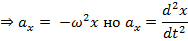
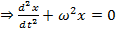: дифференциальное уравнение свободных гармонических колебаний.