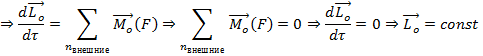Основное уравнение вращательного движения.

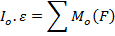
Где: сумма 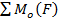– суммарный момент всех внешних сил действуют на тело проекции по ось врещения

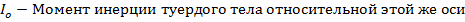
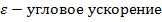
Момент инерции облядает свйством адитивносит момент инерции систем относит оси вращения равно сумме моментов инерций тел состав системй относительно той же оси вращения

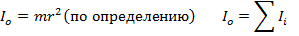
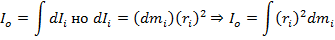
1) Расчет момента инерции тонкого кольца массой m и радиусом R относително оси перпендикулярно плоскости кольцо и проход через центр.

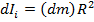
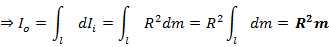
2) Момент инерции сплошного диска массой m и радиусом R , относительно той де оси что и в П1. Разобьем диск на n колце

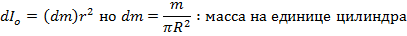
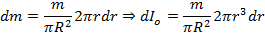
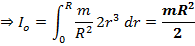
3) Момент инерции стержня относително перпендикулярно через его центр

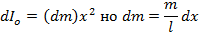
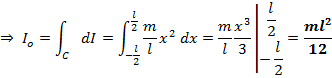
4) Момент инерции тонкого стержня относительно оси перепендикулярно и проход через начало стержня

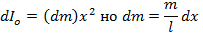
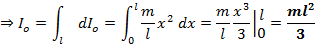
5) Момент инерции тонкой сферической оболочки

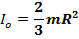
6) Момент инерции крепкой шферы

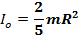
7)Момент инерции тонкого диска

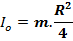
8) Инерции тонкого обруча

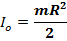
Теорема Гюйгенса – Штейнеф: Момент инерции тела относително какой либооси равен моменту инерции этого тела относително оси параметра данной и проход через центр масс тела + произведение масс тела на квадрат расстояние между осями

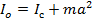
Пример: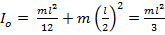

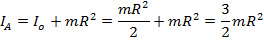
Рассмотрим вращение материальных точек относительно наподвижной оси.

Проекция на оси.

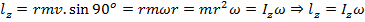
Пусть имеем систему материальных точек, которые вращаются относительно ось z.

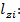проекция l_z на Oz

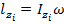
Просуммируем выше уравнение, то получили

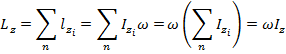
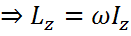
Момент импульса системы относително неподвижной оси равно момент инерции относително той же оси на угловой скорости.

При вращении твердых тел.

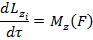
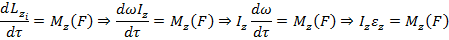
Основное уравнение динамического вращателного движения.

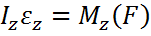
13) Момент импульса точки,тела, системы материальных точек относительно полюса.Уравнение моментов. Закон сохранения момента импульса, условие его применимости.

Пусть имеем материальную точку массой m, которой движется вектором 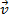, обладает импульса 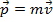. Пусть импульс 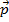нарпавлено от нас. Пусть положение этой точки относително не подвижной по точку О, характеризует вектор 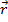в данны момент вращении.

Плоскость образуется векторам 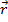и .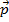

Тогда по определению момент импульс 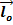точки относительно неподвижной оси называется векторное произведение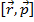

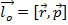
1) 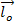перпендикулярно плосскости образована вескторами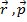

2) 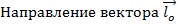определяется по правилу буравинка

3) Величина момента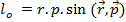

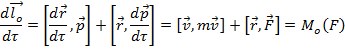
Тогда момент системы материальных точекотносительно неподвижной оси называется “ Геометрический суммарный” момент импульса точек состовляющий системы относительно той же неподвижной оси.

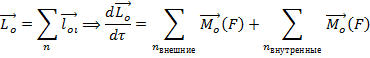
Уравнение моментов

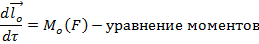
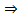Производная момента импульса материальной точки оносительно неподвижной оси по времени равна момент сила действуйщий на точку относително той же ось.

Суммарно всех внутренных сил относително в любой точки равно нулью. Поэтому