О коэффициенте жесткости пружины

Коэффициент жесткости зависит от длины пружины 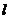и площади поперечного сечения S витков пружины, а также от материала, из которого изготовлена пружина:

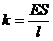, Е - модуль Юнга материала пружины

Если пружина становится вдвое короче (при прежнем S), то k увеличивается в 2 раза, если S становится вдвое меньше (при постоянном 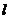), то k уменьшается вдвое.

Эта формула пригодится при определении периода колебаний пружинного маятника.

ВСЕМИРНОЕ ТЯГОТЕНИЕ

1. Ньютон, 1687, закон: сила тяготения 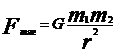, m₁, m₂ – массы, r– расстояние. Гравитационная постоянная 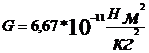есть сила притяжения масс по 1 кг. на расстоянии 1 м. Формула справедлива для материальных точек и тел сферической формы.

2. Ускорение свободного падения (ускорение силы тяжести, напряженность поля тяготения) g – ускорение, сообщаемое телу силой тяготения. По II Закону Ньютона .

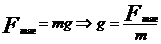На поверхности Земли 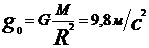, где M, R – масса и радиус Земли.

На высоте h над поверхностью Земли 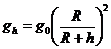, на глубине h под поверхностью Земли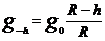

3. Потенциальная энергия тела, поднятого на высоту h над поверхностью Земли, 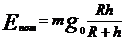(при условии, что на поверхности Земли потенциальная энергия принимается за нуль)

При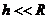

4. I космическая скорость – скорость, которую нужно сообщить телу, чтобы оно стало искусственным спутником Земли (ИСЗ).

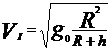, h - высота орбиты над поверхностью Земли

При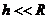

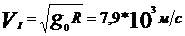
5. II космическая скорость – скорость, которую нужно сообщить телу, чтобы оно преодолело притяжение Земли и удалилось на (практически попадает в поле притяжения Солнца и становится искусственной планетой)

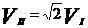, при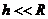

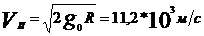
6. III Закон Кеплера – квадраты периодов обращения планет относятся как кубы больших полуосей орбит (планеты движутся по эллипсам)

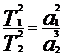, a₁, a₂ – большие полуоси

- № 276

НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА (НИСО)

1. Системы отсчета, движущиеся с ускорением, называются НИСО.

2. Чтобы записать II Закон Ньютона в НИСО в такой же форме, как и в

ИСО необходимо к реальным силам добавить, так называемые, силы инерции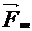

Силы инерции действуют только в НИСО, как только система отсчета становится ИСО, силы инерции исчезают (поэтому их иногда называют пассивными силами).

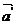II Закон Ньютона в НИСО: , где и 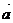– соответственно ускорение в НИСО и ИСО.

3. Если НИСО движется поступательно, то 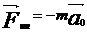, где 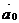– ускорение, с которым движется НИСО, т.о.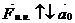

4. Если НИСО является вращающейся (например Земля, вращающаяся вокруг своей оси), то 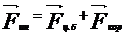, где 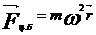– центробежная сила инерции, ω – угловая скорость вращения НИСО, 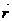– радиус-вектор тела (по модулю расстояние от оси вращения); 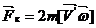– Кориолисова сила инерции, 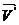- скорость, с которой движется тело в НИСО.

ДИНАМИКА ТЕЛ ПЕРЕМЕННОЙ МАССЫ

УРАВНЕНИЕ МЕЩЕРСКОГО

1. Рассмотрим движение тела, масса которого в процессе движения изменяется (на примере автомобиля, поливающего водой улицу). Для описания такого движения нужно применить II Закон Ньютона в общем виде:

=

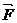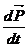
2. Пусть за время dt масса автомобиля изменилась на dm, тогда величина 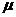= 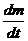называется расходом воды. Обозначим через m и 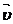массу и скорость автомобиля в данный момент времени, а через 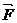силу тяги двигателя автомобиля. Скорость воды, выливающейся из автомобиля, обозначим через .

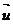Тогда уравнение, описывающее движение автомобиля имеет вид:

m 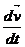= 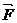- - 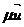уравнение Мещерского

3. Величина (- 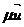) называется реактивной силой, она направлена против направления выброса воды из автомобиля. Она действует до тех пор, пока выбрасывается вода из автомобиля.

ФОРМУЛА ЦИОЛКОВСКОГО

1. Применим уравнение Мещерского для случая движения ракеты. При этом нужно учесть 2 фактора:

а) реактивная сила по величине больше намного всех остальных сил, действующих на ракету, и ими пренебрегают;

б) продукты сгорания топлива выбрасываются не по ходу движения ракеты, а в обратную сторону.

Тогда уравнение Мещерского примет вид:

m= 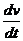= 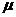u

2. Масса ракеты в процессе движения со временем изменяется:

m=m₀e^-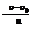

m и m₀ – масса ракеты в данный момент времени и в начальный момент времен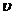и, и 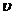₀– скорость ракеты в данный момент времени и в начальный момент времени, u– скорость, с которой продукты сгорания топлива выбрасываются из ракеты.

3. Скорость, которую достигнет ракета через время t после старта, вычисляется по формуле: 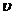= 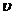₀+u ln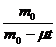, где 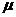- изменение массы ракеты за единицу времени (расход топлива), а остальные обозначения такие же, как и в формуле для массы в пункте 2.

4. Приведенные формулы называются формулами Циолковского.

КОЛЕБАНИЯ И ВОЛНЫ