Ур-ние эл-м. волн. Энергия волн. Излучение диполя

Векторы напряженностей Е и Н переменного эл-м. поля удовлетв. волновому ур-нию

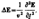
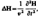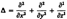где — оператор Лапласа, v — фазовая скорость.

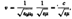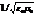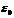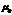Фазовая скорость эл-м-ых волн равна где с = , и -электр. и магнитная постоянные, e и m - электр. и магнитная проницаемости среды.

При вычислении скорости распространения эл-м. поля по ф-ле получается результат, совпадающий с эксперим. данными, если учитывать зависимость e и m от частоты. Совпадение размерного коэффициента в со скоростью распространения света в вакууме указывает на глубокую связь между электром. и оптическими явлениями, позволившую Максвеллу создать электромаг. теорию света, согласно которой свет представ­ляет собой эл.м. волны.

Следствием теории Максвелла является поперечность эл-м-ых волн: век­торы Е и Н напряженностей электр. и магнит. полей волны взаимно перпендикул. и лежат в плоскости, перпендикулярной вектору v скорости рас­пространения волны, причем векторы Е, Н и v образуют правовинтовую систему. Из ур-ний Максвелла следует, что в электром. волне векторы Е и Н все­гда колеблются в одинаковых фазах причем мгновенные значения Е и Н в любой точке связаны соотношением

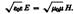Сл-но, Е и Н одновременно достигают максимума, одновременно обраща­ются в нуль и т. д.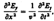

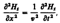
где индексы у и z при Е и Н подчеркивают то, что векторы Е и Н направлены вдоль взаимно перпендик. осей y и z.

Уравнениям удовлетв. плоские монохроматические эл.м. волны (эл.м. волны одной строго определенной частоты), описываемые ур-ниями 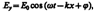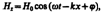где E₀ и Н₀ -амплитуды напряженностей электр. и магнит. полей волны, w — круговая частота волны, k=w/v — волновое число, j — на­чальные фазы колебаний в точках с координатой х=0. j одинаково, так как колебания электрического и магнитного векторов в электромаг­нитной волне происходят в одинаковых фазах.

Объемная плотность w энергии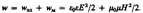

Т.к. w_эл = w_м. То 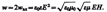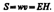Т.к. векторы Е и Н взаимно перпендик., то [ЕН] совпада­ет с направлением переноса энергии, а модуль этого вектора равен ЕН.Вектор плотности потока электромагнитной энергии называетсявектором Умова — Пойнтинга: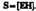

Импульс эл-м. поля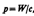

где W — энергия эл-м. поля. Выражая импульс как р=тс (поле в ваку­уме распространяется со скоростью с), получим р=тс= W/c, откуда 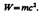Это соотношение между массой и энергией эл-м. поля является универ­сальным законом природы.

Излучение диполя.

Простейшим излучателем эл-м-ых волн является электрический диполь, электрический момент которого изменяется во времени по гармоническому закону 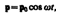где р₀ — амплитуда вектора р. Примером - система, состоящая из покоящегося положительного заряда +Q и отрицательного заряда –Q, гармонически колеблющегося вдоль направления р с частотой w.

Характер эл-м. поля диполя зависит от выбора рассматриваемой точки. Волновая зона диполя — точки пространства, отстоящие от диполя на расстояниях r, превышающих длину волны (r>>l), - картина эл-м. поля диполя сильно упрощается. Это связано с тем, что в волновой зоне диполя практически остаются только «отпочковавшиеся» от диполя, свободно распространяющиеся поля, в то время как поля, колеблющиеся вместе с диполем и имеющие более сложную структуру, сосредоточены в области расстояний r < l.

Если волна распространяется в однородной изотропной среде, то время прохожде­ния волны до точек, удаленных от диполя на расстояние r, одинаково. Поэтому во всех точках сферы, центр которой совпадает с диполем, фаза колебаний одинакова, т. е. в волновой зоне волновой фронт будет сферическим и, следовательно, волна, излуча­емая диполем, есть сферическая волна.

3. Развитие представлений о природе света

Основные законы оптики известны еще с древних веков. Платон установил закон прямолинейного распространения и закон отражения света. Аристо­тель и Птолемей изучали преломление света. Первые представления о природе света возникли у древних греков и египтян. В конце XVII в. на основе многовекового опыта и развития представлений о свете возниклидве теории света: корпускулярная (И. Ньютон) и волновая (Р. Гук и X. Гюйгенс)

Согласно корпускулярной теории (теории истечения), свет представляет собой поток частиц (корпускул), испускаемых светящимися телами и летящих по прямолиней­ным траекториям.

Согласно волновой теории,свет представляет собой упругую волну, распространяющуюся в особой среде — эфире. Эфир заполняет все мировое пространство, пронизывает все тела и обладает механическими свойствами — упругостью и плотностью. Согласно Гюй­генсу, большая скорость распространения света обусловлена особыми свойствами эфира.

Волновая теория основывается на принципе Гюйгенса: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих воли дает положе­ние волнового фронта в следующий момент времени. волновым фронтом называется геометрическое место точек, до которых доходят колебания к моменту времени t. видим, что волновая теория приводит к выводу, отличному от вывода теории Ньютона. По теории Гюйгенса, v<c, т. е. скорость распространения света в среде должна быть всегда меньше скорости его распространения в вакууме.

Таким образом, к началу XVIII в. сущ. два противоположных подхода к объяснению природы света: корпускулярная теория Ньютона и волновая теория Гюйгенса. Эксперименталь­ное д-во справедливости волновой теории было получено в 1851 г., когда Э. Фуко К началу XIX столетия корпускулярная теория была полностью отвергнута и восторжествовала волновая теория. Заслуга в этом английскому физику Т. Юнгу, исследовавшему явления дифракции и интерференции, и французскому физи­ку О. Френелю , дополнившему принцип Гюйгенса и объяснившему эти явления.

Наука о свете накапливала экспериментальные данные, свидетельствующие о взаимосвязи световых, электрических и магнитных явлений, что позволило Максвеллу в 70-х годах прошлого столетия создать эл-м. теорию света. Согласно эл-м. теории Максвелла .

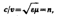где с и v -скорости распространения света в вакууме и в среде с диэлектрической проницаемостью e и магнитной проницаемостью m. Это соотноше­ние связывает оптические, электрические и магнитные постоянные вещества. По Макс­веллу, e и m- величины, не зависящие от длины волны света, поэтому электромагнит­ная теория не могла объяснить явление дисперсии (зависимость показателя преломле­ния от длины волны). Эта трудность была преодолена в конце XIXв. Лоренцем, предложившим электронную теорию, согласно которой диэлектрическая проницае­мость e зависит от длины волны падающего света. Теория Лоренца ввела представле­ние об электронах, колеблющихся внутри атома, и позволила объяснить явления испускания и поглощения света веществом.

Теория Максвелла не смогла объ­яснить процессов испускания и поглощения света. Лоренца, в свою очередь, не смогла объяснить многие явления, связанные с взаимодействием света с веществом. Эти противоречия были преодолены благодаря гипотезе немецкого физика М. Планка, согласно которой излучение и поглощение света происходит не непрерывно, а дискретно, т. е. определенными порциями (квантами), энергия которых определяется частотой n: 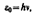где h — постоянная Планка.

Эйнштейн в 1905 г. создал квантовую теорию света, согласно которой не только излучение света, но и его распространение происходит в виде потока световых квантов — фотонов. Свет имеет сложную природу. Он представляет собой единство противоположных видов движения — корпускулярного (квантового) и волнового (электромагнитного). Длительный путь развития привел к современным представлениям о двойственной корпускулярно-волновой природе света.

4. Когерентность и монохроматичность световых волн. Интерференция света.

Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны - волны амплитуда, частота и начальная фаза которых остаются постоянными неограниченно долго. Ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Прерывистое излучение света атомами в виде отдельных коротких импульсов называется волновым цугом.

Любой немонохроматический свет можно представить в виде совокупности сменя­ющих друг друга независимых гармонических цугов. Средняя продолжительность одного цуга t_ког наз. временем когерентности. Когерентность существует только в пределах одного цуга, и время когерентности не может превышать время излучения, т. е. t_ког < t. Если волна распространяется в однородной среде, то фаза колебаний в определен­ной точке пространства сохраняется только в течение времени когерентности t_ког. За это время волна распространяется в вакууме на расстояние l_ког =сt_ког, наз. длиной когерентности (илидлиной цуга). Чем ближе волна к монохроматической, тем меньше ширина спектра ее частот и больше ее время когерентности t_ког, и длина когерентности l_ког. Когерентность колебаний, которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности волн, наз. временнóй когерентностью.

Два источника, размеры и взаимное расположение которых позволяют наблюдать интерференцию, называютсяпространственно-когерентными. Радиусом когерентности(илидлиной пространственной когерентности) наз. максимальное поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции. Пространственная когерентность определяется ради­усом когерентности.

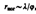где l — длина волны света, j — угловой размер источника. Интерференция света

Предположим, что две монохроматические световые волны, накладываясь друг на друга, возбуждают в определенной точке пространства колебания одинакового направ­ления: х₁=А₁ cos(w t + j₁) и x₂ = A₂ cos(w t + j₂). Под х понимают напряженность элект­рического Е или магнитного Н полей волны; векторы Е и Н колеблются во взаимно перпендикулярных плоскостях. Напряженности электр. и магнит­ного полей подчиняются принципу суперпозиции . Амплитуда резуль­тирующего колебания в данной точке 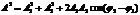Так как волны когерентны, то cos(j₂ — j₁) имеет постоянное во времени значение, поэтому интенсивность результирующей волны (I ~ А²)

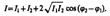Сл-но, при наложении двух (или нескольких) коге­рентных световых волн происходит пространственное перераспределение светового потока, возникают максимумы, мини­мумы интенсивности. Это явление наз.интерференцией света.

Для некогерентных волн разность j₂—j₁ непрерывно изменяется, поэтому среднее во времени значение cos(j₂—j₁) равно нулю, и интенсивность результирующей волны всюду одинакова

Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга, и наблюдается интерференци­онная картина.

Произведение геомет­рической длины s пути световой волны в данной среде на показатель n преломления этой среды называетсяоптической длиной пути L, a D = L₂ – L₁ — разность оптических длин проходимых волнами путей — называетсяоптической разностью хода.Если оптическая разность хода равна целому числу длин волн в вакууме 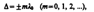то d = ±2тp, и колебания, возбуждаемые в точке М обеими волнами, будут проис­ходить в одинаковой фазе. Сл-но, является условием интерференционного максимума.

Если оптическая разность ход 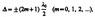то d = ±2(т+1)p, и колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе. Сл-но, является условием интерференционного минимума.

5. Методы наблюдений интерференции света1. Метод Юнга. Источником света служит ярко освещенная щель S , от которой световая волна падает на две узкие равноудаленные щели S₁ и S₂, параллель­ные щели S. Таким образом, щели S₁ и S₂ играют роль когерентных источников.

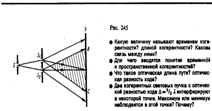
Интерференционная картина (область ВС) наблюдается на экране (Э), расположенном на некотором расстоянии параллельно S₁ и S₂.

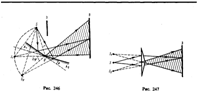
2. Зеркала Френеля. Свет от источника S падает расходящимся пучком на два плоских зеркала А₁О и А₂О, расположенных относительно друг друга под углом, лишь немного отличающимся от 180° (угол j мал). Используя правила построения изображения в плоских зеркалах, можно показать, что и источник, и его изображения S₁ и S₂ (угловое расстояние между которыми равно 2j) лежат на одной и той же окружности радиуса r с центром в О (точка соприкосновения зеркал).

Световые пучки, отразившиеся от обоих зеркал, можно считать выходящими из мнимых источников S₁ и S₂, являющихся мнимыми изображениями S в зеркалах. Мнимые источники S₁ и S₂ взаимно когерентны, и исходящие из них световые пучки, встречаясь друг с другом, интерферируют в области взаимного перекрывания (на рис. 246 она заштрихована). Можно показать, что максимальный угол расхожде­ния перекрывающихся пучков не может быть больше 2j. Интерференционная карти­на наблюдается на экране (Э), защищенном от прямого попадания света заслон­кой (З).

3. Бипризма Френеля. Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S (рис. 247) преломляется в обеих призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых источников S₁ и S₂, являющихся когерентными. Таким образом, на поверхности экрана (в заштрихованной области) происходит наложение когерентных пучков и наблюдается интерференция.

12. Разрешающая способность оптических приборов.Согласнокритерию Рэлея, изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий с равными интенсивностями и одинаковыми симметричными контурами разрешимы (разделены для восприятия), если центральный максимум дифракционной картины от одного источника (линии) совпадает с первым минимумом дифракционной картины от другого.

1. Разрешающая способность объектива. Если на объектив падает свет от двух удаленных точечных источников S₁ и S₂ (например, звезд) с некоторым угловым расстоянием dy, то вследствие дифракции световых волн на краях диафрагмы, ограни­чивающей объектив, в его фокальной плоскости вместо двух точек наблюдаются максимумы, окруженные чередующимися темными и светлыми кольцами (рис. 266).Можно доказать, что две близлежащие звезды, наблюдаемые в объективе в монохро­матическом свете, разрешимы, если угловое расстояние между ними

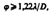где l — длина волны света, D — диаметр объектива.

Разрешающей способностью (разрешающей силой) объектива называется величина

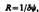где dy — наименьшее угловое расстояние между двумя точками, при котором они еще оптическим прибором разрешаются. разрешающая способность объектива 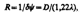т. е. зависит от его диаметра и длины волны света.

Разрешающей способностью спектрального прибораназывают безразмерную ве­личину 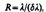где dl — абсолютное значение минимальной разности длин волн двух соседних спект­ральных линий, при которой эти линии регистрируются раздельно.

2. Разрешающая способность дифракционной решетки.Пусть максимум т-го поряд­ка для длины волны l₂ наблюдается под углом j, т. е., согласно (180.3), dsinj=ml₂. При переходе от максимума к соседнему минимуму разность хода меняется на l/N , где N — число щелей решетки. Сл-но,минимум l₁, наблюдаемый под углом j_min, удовлетворяет условию dsinj_min=ml₁+l₁/N. По критерию Рэлея, j =j_min, т. е. ml₂=ml₁+l₁/N или l₂/(l₂–l₁)=mN. Tax как l₁ и l₂ близки между собой, т. е. l₂–l₁=dl то 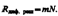Таким образом, разрешающая способность дифракционной решетки пропорциональна порядку m спектра и числу N щелей, т. е. при заданном числе щелей увеличивается при переходе к большим значениям порядка m интерференции. Современные дифракцион­ные решетки обладают довольно высокой разрешающей способностью (до 2×10⁵).

6. Интерференция света в тонких пленках

Пусть на плоскопараллельную прозрачную пленку с показателем преломления п и толщиной d под углом i падает плоская монохроматическая волна На поверхности пленки в точке О луч разделится на два: частично отразится от верхней поверхности пленки, а частично преломится. Преломленный луч, дойдя до точки С, частично преломится в воздух (п₀=1), а частич­но отразится и пойдет к точке В. Здесь он опять частично отразится и преломится, выходя в воздух под углом i. Вышедшие из пленки лучи 1 и 2 когерентны, если оптическая разность их хода мала по сравнению с длиной когерентности падающей волны. Если на их пути поставить собирающую линзу, то они сойдутся в одной из точек Р фокальной плоскости линзы. В р-те возникает интерф. картина, которая опреде­ляется оптической разностью хода между интерферирующими лучами.

Оптическая разность хода, возникающая между двумя интерферирующими лучами от точки О до плоскости АВ,

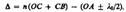
где показатель преломления окружающей пленку среды принят равным 1, а член ± l₀/2 обусловлен потерей полуволны при отражении света от границы раздела. Если п>n₀, то потеря полуволны произойдет в точке О и вышеупомянутый член будет иметь знак минус; если же п<n₀, то потеря полуволны произойдет в точке С и l₀/2 будет иметь знак плюс. Согласно рис. 249, OC=CB=d/cosr, OA = OB sin i = 2d tg r sin i. Учитывая для данного случая закон преломления sin i = n sin r, получим

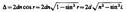
С учетом потери полуволны для оптической разности хода получим 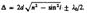Для случая, изображенного на рис. (п>n₀),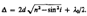

В точке Р будет интерференционный максимум, если

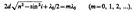и минимум, если

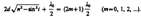Интерфер., , наблюдается, только если удвоенная толщина пластинки меньше длины когерентности падающей волны.

1. Полосы равного наклона (интерференция от плоскопараллельной пластинки). интерф. карт. в плоскопараллельных пластинках (пленках) определяется величинами l₀, d, п и i. Для данных l₀, d, и n каждому наклону i лучей соответствует своя интерференционная полоса. Ин­терференционные полосы, возникающие в р-те наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называютсяполосами равного наклона.

Лучи 1' и 1", отразившиеся от верхней и нижней граней пластинки , параллельны друг другу, так как пластинка плоскопараллельна. Следовательно, ин­терферирующие лучи 1' и 1" «пересекаются» только в бесконечности, поэтому говорят, что полосы равного наклона локализованы в бесконечности. Для их наблюдения исполь­зуют собирающую линзу и экран (Э), расположенный в фокальной плоскости линзы. Параллельные лучи 1' и 1" соберутся в фокусе F линзы в эту же точку придут и другие лучи, параллельные лучу 1, в р-те чего увеличивается общая интенсивность. Лучи 3, наклоненные под другим углом, соберутся в другой точке Р фокальной плоскости линзы. Легко показать, что если оптическая ось линзы перпендикулярна поверхности пластинки, то полосы равного наклона будут иметь вид концентрических колец с цент­ром в фокусе линзы.

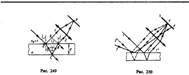
7.Клинообразная пленка. Полосы равной толщины (интерференция от пластинки переменной толщины).Пусть на клин (угол a между боковыми гранями мал) падает плоская волна, направле­ние распространения которой совпадает с параллельными лучами 1 и 2. Из всех лучей, на которые разделяется падающий луч 1, рассмотрим лучи 1' и 1", отразившиеся от верхней и нижней поверхностей клина. При определенном взаимном положении клина и линзы лучи 1' и 1" пересекутся в некоторой точке А, являющейся изображением точки В. Так как лучи 1' и 1" когерентны, они будут интерферировать. Если источник расположен довольно далеко от поверхности клина и угол a ничтожно мал, то оптическая разность хода между интерферирующими лучами 1' и 1" может быть с достаточной степенью точности вычислена по ф-ле , где d — тол­щина клина в месте падения на него луча. Лучи 2' и 2", образовавшиеся при делении луча 2, падающего в другую точку клина, собираются линзой в точке А'. Оптическая разность хода уже определяется толщиной d'. Таким образом, на экране возникает система интерференционных полос. Каждая из полос возникает при отражении от мест пластинки, имеющих одинаковую толщину (в общем случае толщина пластинки может изменяться произвольно). Интерференционные полосы, возникающие в р-те интерференции от мест одинаковой толщины, называются полосами равной толщины.

Так как верхняя и нижняя грани клина не параллельны между собой, то лучи 1' и 1" (2' и 2") пересекаются вблизи пластинки, на рис. случае — над ней (при другой конфигурации клина они могут пересекаться и под пластинкой). Таким образом, полосы равной толщины локализованы вблизи поверхности клина. Если свет падает на пластинку нормально, то полосы равной толщины локализуются на верхней поверхности клина.

8. Принцип Гюйгенса — Френеля

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле — любое отклонение распространения волн вблизи препятст­вий от законов геометрической оптики.

Явление дифракции объясняется с помощью принципа Гюйгенса -каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени.

Принцип Гюйгенса решает задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а Сл-но, и об интенсивности волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физ. смысл, дополнив его идеей интерференции вторичных волн.

Согласнопринципу Гюйгенса — Френеля, световая волна, возбуждаемая каким-ли­бо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверх­ностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех коге­рентных вторичных волн. Френель исключил возможность возникновения обратных вторичных волн и предположил, что если между источником и точкой наблюдения находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии — такая же, как при отсутствии экрана.

Метод зон Френеля.

Принцип Гюйгенса — Френеля в рамках волновой теории должен был ответить на вопрос о прямолинейном распространении света. Френель решил эту задачу, рассмот­рев взаимную интерференцию вторичных волн и применив прием, получивший назва­ние метода зон Френеля.

Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде из точечного источника S . Согласно принципу Гюйген­са — Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Ф, являющейся поверхностью фронта волны, идущей из S (поверхность сферы с центром S). Френель разбил волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отличались на l/2. Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точ­ке М сферы радиусами b + , b + 2 , b + 3 , ... . Т.к. колебания от соседних зон проходят до точки М расстояния, отличающиеся на l/2, то в точку М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М

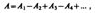где А₁, А₂, ... — амплитуды колебаний, возбуждаемых 1-й, 2-й, ..., т-й зонами.

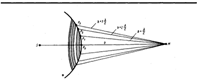
построение зон Френеля разбивает волно­вую поверхность сферической волны на равные зоны.

Согласно предположению Френеля, действие отдельных зон в точке М тем меньше, чем больше угол j_т (рис. 258) между нормалью n к поверхности зоны и направлением на М, т. е. действие зон постепенно убывает от центральной (около Р₀) к периферичес­ким. Кроме того, интенсивность излучения в направлении точки М уменьшается с ростом т и вследствие увеличения расстояния от зоны до точки М. Учитывая оба этих фактора, можем записать

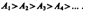Общее число зон Френеля, умещающихся на полусфере, очень велико; например при а=b=10 см и l=0,5мкм 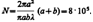Поэтому в качестве допустимо­го приближения можно считать, что амплитуда колебания А_m от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон, т. е.

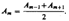Тогда выражение можно записать в виде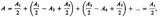

так как выражения, стоящие в скобках, согласно (177.5), равны нулю, а оставшаяся часть от амплитуды последней зоны ±А_m/2 ничтожно мала.

в однородной среде.

9. Дифракция Френеля на круглом отверстии и диске

Рассмотримдифракцию в сходящихся лучах, илидифракцию Френеля, осуществляемую в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию.

1. Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифрак­ционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259). Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами 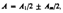знак плюс соответствует нечетным m и минус -четным т.

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсив­ность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А=А₁, т. е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если m нечетное — то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.

2. Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром диска (рис). В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна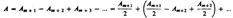

или 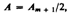Т.к.выражения, стоящие в скобках, равны нулю. Сл-но, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий поло­вине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в мак­симумах убывает с расстоянием от центра картины.

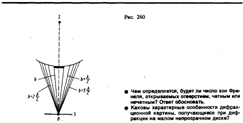
С увеличением радиуса диска первая открытая зона Френеля удаляется от точки В и увеличивается угол j_т между нормалью к поверхности этой зоны и направлением на точку В. В результате интенсивность центрального максимума с увеличением размеров диска уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место весьма слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распрост­раняющимся прямолинейно.

10. Дифракция Фраунгофера на одной щели.физик И. Фраунгофер рассм. дифракцию плоских световых волн,илидифракцию в параллельных лучах. Дифракция Фраунгофера,наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию.

Рассм. дифракцию Фраунгофера от бесконечно длинной щели. Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а. Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении j, 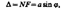где F — основание перпендикуляра, опущенного из точки М на луч ND.

Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна l/2, т. е. всего на ширине щели уместится D:l/2 зон. Т.к. свет на щель падает нормально, то плоскость щели совпадает с волновым фронтом; Сл-но, все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, Т.к.выбранные зоны Френеля имеют оди­наковые площади и одинаково наклонены к направлению наблюдения.

Из выражения вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла j. От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, Т.к.колебания от каждой пары соседних зон взаимно гасят друг друга. Сл-но, если число зон Френеля четное, то

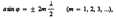и в точке В наблюдаетсядифракционный минимум(полная темнота), если же число зон Френеля нечетное, то

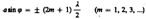и набл. дифракционный максимум. В направлении j=0 щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интен­сивностью, т. е. в точке В₀ наблюдается центральный дифракционный максимум.

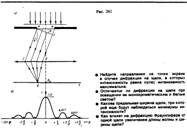
Положение дифракционных максимумов зависит от длины волны l, поэтому рассмотренная выше дифракционная картина имеет место лишь для монохроматичес­кого света. При освещении щели белым светом центральный максимум наблюдается в виде белой полоски; он общий для всех длин волн (при j =0 разность хода равна нулю для всех l). Боковые максимумы радужно окрашены, Т.к.условие максимума при любых т различно для разных l. Таким образом, справа и слева от центрального максимума наблюдаются максимумы первого (m=1), второго (т=2) и других поряд­ков, обращенные фиолетовым краем к центру дифракционной картины. Однако они настолько расплывчаты, что отчетливого разделения различных длин волн с помощью дифракции на одной щели получить невозможно.

Дифракционная решетка.

Одномерная дифракционная решетка — систему параллельных щелей рав­ной ширины, лежащих в одной плоскости и разделенных равными по ширине непроз­рачными промежутками. Дифрак. карт. на решетке определяется как результат взаимной ин­терференции волн, идущих от всех щелей, т. е. в дифракционной решетке осуществля­ется многолучевая интерференция когерентных дифрагированных пучков света, иду­щих от всех щелей.

Рассмотрим дифра