Дифференциальное уравнение движения физического маятника

10.

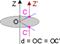Рассмотрим вращение стержня вокруг некоторой оси Z (см. рис. 6.8). Кинетическую энергию стержня можно представить в виде:

E_к = I·w²/2. где I - момент инерции стержня относительно оси Z. Учитывая, что для случая движения по окружности справедливо соотношение V_c = d·w, и приравнивая приведенные выше выражения для кинетической энергии стержня, получим уравнение, которое является выражением теоремыШтейнера:

I = I_c + m·d²/2. Момент инерции тела относительно произвольной оси вращения равен его моменту инерции относительно параллельной оси, проходящей через центр масс тела, плюс произведение массы на квадрат расстояния между этими осями.

11. Кинетическая энергия материальной точки и абсолютно твердого тела.

Кинетической энергией материальной точки называется скалярная величина, которая равняется половине произведения массы точки на квадрат ее скорости.Кинетическаяэнергия:характеризует и поступательное и вращательное движения;не зависит от направления движения точек системы и не характеризует изменение этих направлений;характеризует действие и внутренних и внешних сил.Кинетическая энергия системы равняется сумме кинетических энергий тел системы. Кинетическая энергия зависит от вида движения тел системы.Кинетическая энергия твёрдого тела.Для твёрдого тела имеет место формула: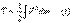

Нужно различать кинетическую энергию твёрдого тела при различных видах его движения.Кинетическая энергия тела твёрдого движущегося оступательно.При поступательном движении, все скорости одинаковы.

12. Работа переменной силы. Если сила или равнодействующая сил изменяет свою величину или направление (движение по криволинейной траектории, причем угол α ≠ 90⁰), то работа ∆А, совершаемая переменной силой F (или Fрез) на конечном участке траектории вычисляется следующим образом.На рисунке 14 представлен график зависимости силы F от пути S. Разобьем весь путь на N участков. Перемещение и действующая сила на каждом участке соответственно равны F _i и ∆ r _i. Тогда работа А, совершаемая силой F, равна алгебраической сумме работ, совершаемых каждой из сил F _i на своем малом участке (Рисунок 14):

А = ∆А₁ + ∆А₂ +....+ ∆А _N = ( F₁∙∆ r₁) + (F ₂∙∆ r₂) + ...+( F _N∙∆ r_N) = 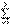( F_i∙∆ r_i),

где i = 1,2...... N - номер элементарного участка траектории.

Мо́щность — физическая величина, равная в общем случае скорости изменения энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.Различают среднюю мощность за промежуток времени 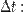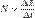и мгновенную мощность в данный момент времени:

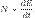
Потенциальными (консервативными) силами называются такие силы, работа которых зависит только от начальных и конечных положений точек их

приложения и не зависит ни от вида траекторий этих точек, ни от законов их движения по траекториям.

Консервативные силы – гравитационные, электростатические.Потенциальные силы создают стационарное поле, в котором работа силы зависит только от начального и конечного положений перемещаемой точки.Если внешние тела, создающие рассматриваемое поле, могут двигаться относительно инерциальной системы, то это поле не будет

стационарным. Но нестационарное поле потенциально, если работа, совершаемая силой F при мгновенном переносе точки ее приложения вдоль любой траектории L, равна нулю.К непотенциальным относятся диссипативные и

гироскопические силы. Диссипативными силами называются силы, суммарная работа которых при любых перемещениях замкнутой системы всегда отрицательна (например, силы трения). Гироскопическими силами называются силы, зависящие от скорости

материальной точки, на которую они действуют, и направленные

перпендикулярно к этой скорости (например, сила Лоренца, действующая со стороны магнитного поля на движущуюся в нем заряженную частицу). Работа гироскопических сил всегда равна нулю.Мощностью (мгновенной мощностью) называется скалярная величина N, равная отношению элементарной работы А к малому промежутку времени dt, в течение которого эта работа совершается.Средней мощностью называется величина<N>, равная отношению работы А, совершаемой за промежуток времени t, к продолжительности этого промежутка

Потенциальной энергией называется часть энергии механической системы, зависящая только от ее конфигурации. Убыль потенциальной энергии при перемещении системы из одного произвольного положения в другое произвольное положение измеряется работой, которую совершают при этом все стационарные потенциальные силы (внешние и внутренние), действующие на систему где W_п(1) и W_п(2) – значения потенциальной энергии системы в начальном и конечном положениях.

При малом изменении конфигурации системы.Для нестационарных потенциальных сил.Потенциальная энергия материальной точки W_п связана с силовой функцией соответствующего потенциального поля соотношением или где С – постоянная интегрирования.

13. Результаты ньютоновских расчетов теперь называют законом всемирного тяготения Ньютона. Согласно этому закону между любой парой тел во Вселенной действует сила взаимного притяжения. Как и все физические законы, он облечен в форму математического уравнения. Если M и m — массы двух тел, а D — расстояние между ними, тогда сила F взаимного гравитационного притяжения между ними равна:

F = GMm/D² где G — гравитационная константа, определяемая экспериментально. В единицах СИ ее значение составляет приблизительно 6,67 × 10^–11.Поле тяготения— физическое поле, через которое осуществляется равитационное взаимодействие

В рамках классической физики гравитационное взаимодействие описывается «законом всемирного тяготения» Ньютона, согласно которому сила гравитационного притяжения между двумя материальными точками с массами m1 и m2 пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними: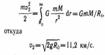

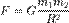
Здесь 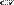— гравитационная постоянная, приблизительно равная 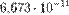м³/(кг с²), 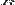— расстояние между точками.

Для расчёта поля в более сложных случаях, когда тяготеющие массы нельзя считать материальными точками, можно воспользоваться тем фактом, что поле ньютоновского тяготения потенциально. Если обозначить плотность вещества ρ, то потенциал поля φ удовлетворяет уравнению Пуассона:

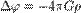Напряжённость гравитацио́нного по́ля — векторная величина, характеризующая гравитационное поле в данной точке и численно равная отношению силы тяготения, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела: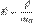

14. Гравитационные поля (поля тяготения) являются потенциальными, то есть работа поля по перемещению тела из точки 1 в точку 2 не зависит от формы траектории, а определяется лишь разностью потенциальных энергий тела в точках 1 и 2 соответственно:

A₁₂ = П₁ – П₂. Из этого равенства ясно, что определенный физический смысл имеет лишь разность потенциальных энергий в различных точках поля.

Космические скорости.

Первая космическая скорость — скорость, которую необходимо придать баллистическому снаряду, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы поместить его на круговую орбиту с радиусом равном радиусу планеты. Иными словами, первая космическая скорость — это скорость, с которой надо бросить камень в горизонтальном направлении, чтобы он больше не упал на Землю. Для вычисления первой космической скорости необходимо рассмотреть равенство центробежной силы и силы тяготения действующих на снаряд на круговой орбите.

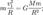
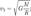
где m — масса снаряда, M — масса планеты, G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость, R — радиус планеты. Подставляя численные значения (для Земли, M = 5,97·1024 кг, R = 6 378 000 м), найдем

7,9 км/с

Первую космическую скорость можно определить через ускорение свободного падения — так как g = GM/R², то .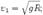

Первой космической скорости недоста точно для того, чтобы тело могло выйти из сферы земного притяжения. Необходимая для этого скорость называется второй кос мической. Второй космической (или пара болической) скоростьюv₂ называют ту наименьшую скорость, которую надо со общить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спут ник Солнца, т. е. чтобы его орбита в поле тяготения Земли стала параболической. Для того чтобы тело (при отсутствии со противления среды) могло преодолеть земное притяжение и уйти в космическое пространство, необходимо, чтобы его кине тическая энергия была равна работе, совершаемой против сил тяготения:Между первой и второй космическими скоростями существует простое соотношение: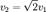

Для того чтобы покинуть пределы солнечной системы, тело должно преодолеть, кроме сил притяжения к земле, также и силы притяжения к Солнцу. Необходимая для этого скорость запуска тела с поверхности Земли называется третьей космической скоростью V3. Скорость V3 зависит от направления запуска. При запуске в направлении орбитального движения Земли эта скорость минимальна и составляет около 17 км/с. При запуске в направлении, противоположном направлению движения Земли, V3 равняется примерно 73 км/с.

15.Абсолютно неупругим ударом, называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело.

Сталкивающиеся тела деформируются, возникают упругие силы и т.д. Однако если удар неупругий то, в конце концов все эти процессы прекращаются, и в дальнейшем оба тела, соединившись вместе, движутся как единое твёрдое тело. Рассмотрим абс. неупругий удар на примере столкновения двух шаров. Пусть они движутся вдоль прямой, соединяющей их центры, со скоростями v₁ и v₂. В этом случае говорят что удар является центральным. Обозначим за V общую скорость шаров после соударения. Закон сохр. Импульса даёт:

m₁v₁+m₂v₂=(m₁+m₂)V V=(m₁v₁+m₂v₂)/(m₁+m₂)

Кин. энергии системы до удара и после: K₁=1/2(m₁v₁²+m₂v₂²) K₂=1/2(m₁+m₂)V

Пользуясь этими выраж. получаем: K₁-K₂=1/2v₁v₂v₁-v₂)

где =m₁m₂/(m₁+m₂) приведенная масса шаров. Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря кин. энергии макроскопического движения, равная половине произведения приведённой массы на квадрат относительной скорости.Абсолютно упругим ударомназывается столкновение тел, в результате которого их внутренние энергии не меняются. Пример: Столкновение бильярдных шаров из слоновой кости, при столкновениях атомных, ядерных частиц. Рассмотрим центральный удар двух шаров, движущ-ся навстречудруг другу:

(m₁v₁²)/2+(m₂ v₂²)/2=(m₁u₁²)/2+(m₂ u₂²)/2

и: m1v1+m₂v₂=m₁u₁+m₂u₂

u1=[(m₁-m₂)v₁+2m₂v₂]/(m₁ +m₂)

u2=[(m₂-m₁)v₂+2m₁v₁]/(m₁+m₂)

При столкновении двух одинаковых абсолютно упругих шаров они просто обмениваются скоростями.

16. Давление в Жидкости. Закон Паскаля

В жидкостях частицы подвижны, поэтому они не имеют собственной формы, но обладают собственным объемом, сопротивляются сжатию и растяжению; не сопротивляются деформации сдвига (свойство текучести).

В покоящейся жидкости существует два вида статического давления: гидростатическое и внешнее. Вследствие притяжения к Земле жидкость оказывает давление на дно и стенки сосуда, а также на тела, находящиеся внутри нее. Давление, обусловленное весом столба жидкости, называется гидростатическим. Давление жидкости на разных высотах различно и не зависит от ориентации площадки, на которую оно производится.

Пусть жидкость находится в цилиндрическом сосуде с площадью сечения S; высота столба жидкости h. Тогда

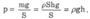
Гидростатическое давление жидкости зависит от плотности р жидкости, от ускорения g свободного падения и от глубины h, на которой находится рассматриваемая точка. Оно не зависит от формы столба жидкости.

Глубина h отсчитывается по вертикали от рассматриваемой точки до уровня свободной поверхности жидкости.

В условиях невесомости гидростатическое давление в жидкости отсутствует, так как в этих условиях жидкость становится невесомой.

На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.

Теорема 1. Архимеда

Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле:

FА = ρжgVпт,

где ρ_ж – плотность жидкости, V_пт – объем погруженной в жидкость части тела.

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

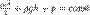
Здесь

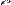— плотность жидкости,

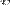— скорость потока,

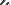— высота, на которой находится рассматриваемый элемент жидкости,

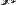— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

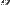— ускорение свободного падения

Закон Бернулли позволяет объяснить эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше, чем на участке трубы большего диаметра, в результате чего наблюдается разница высот столбов жидкости 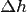; бо́льшая часть этого перепада давлений обусловлена изменением скорости течения жидкости, и может быть вычислена по уравнению Бернулли

17.Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Различают динамическую вязкость (единицы измерения: Па·с = 10 пуаз) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера).

Прибор для измерения вязкости называется вискозиметром.

ДВИЖЕНИЕ ТЕЛ В ЖИДКОСТЯХ И ГАЗАХ Всем реальным жидкостям присуща вязкость или внутреннее трение, что приводит к появлению у них принципиально новых свойств. В частности, возникшее в жидкости движение после прекращения действия причин, его вызвавших, постепенно замедляется. При движении тела в такой жидкости на него действуют силы. Равнодействующую этих сил обозначим через 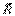. Силу 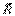можно разложить на две составляющих (рис. 6.5): 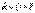. Силу 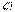называют лобовым сопротивлением, а 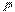– подъемной силой.Если жидкость обладает вязкостью, то очень тонкий слой жидкости прилипает к поверхности тела и движется с ним как одно целое, увлекая за собой из-за трения последующие слои. По мере удаления от тела скорость уменьшается, то есть тело оказывается окруженным пограничным слоем жидкости, в котором скорость изменяется в направлении, перпендикулярном скорости. В нем действуют силы трения, которые в конечном итоге оказываются приложенными к телу и приводят к лобовому сопротивлению. Кроме того, из-за сил трения поток отрывается от поверхности тела, в результате чего позади тела возникают вихри. Вихри уносятся потоком и постепенно затухают вследствие трения. Давление в образующейся за потоком вихревой области оказывается пониженным, поэтому результирующая сил давления будет отлична от нуля, что в свою очередь обусловливает лобовое сопротивление.

18.Под действием внешних сил тела меняют свою форму и размеры. Такие изменения называются деформациями.Различаются упругие и пластические деформации. Если после прекращения приложенных сил деформация исчезает, то деформация является упругой, а если не исчезает – пластической.энергия упругой деформации./Модуль Юнга (модуль упругости)— физическая величина, характеризующая свойства материала сопротивляться

растяжению/сжатию при упругой деформации^[1]. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях.

Модуль Юнга рассчитывается следующим образом:

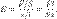
где:

E — модуль упругости,

F — сила,

S — площадь поверхности, по которой распределено действие силы,

l — длина деформируемого стержня,

x — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).

Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне: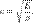

где 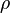— плотность вещества.

Деформированное тело может совершить работу, так как оно обладает запасом потенциальной энергии, называемой упругой энергией. Она равна работе сил, затраченной на деформацию тела, не увеличивая его кинетической энергии. Вычислим теперь энергию упругой деформации стержня. Приложим к стержню растягивающую силу

,

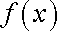
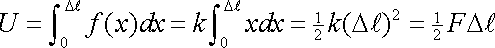
Энергия упругой деформации распределена по всему объему тела.

Энергия 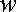, приходящая на единицу объема тела, называемая объемной плотностью упругой энергии, равна:

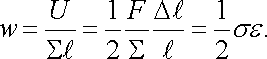
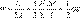
Под действием приложенной силы изменяются не только продольные, но и поперечные размеры стержня. Отношение относительного поперечного сжатия к соответствующему продольному удлинению называется

коэффициентом Пуассона:

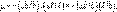
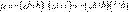
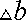
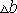
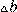
Заметим, что и

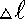
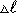
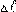
всегда имеют противоположные знаки – при растяжении

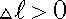
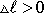
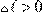
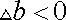
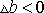
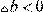
, , а при сжатии – наоборот.

19.Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при

колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии.Характеристики

Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, 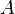(м) Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), 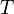(с) Частота — число колебаний в единицу времени, 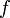(Гц, с⁻¹).

Период колебаний 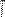и частота 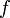— обратные величины;

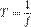и 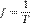В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота 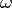(рад/с, Гц, с⁻¹), показывающая число колебаний за 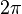единиц времени:

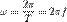Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения метр.Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.Скорость и ускорение точки, совершающей гармонические колебания

Колебательная скорость — величина, равная произведению амплитуды колебаний частиц среды, через которую проходит периодическая звуковая волна, на угловую частоту:v = Aω Единица измерения — метр в секунду (м/с). Для синусоидальной волны колебательная скорость равна амплитуде скорости колеблющихся частиц среды.

Ускорение колебаний аменяется во времени по закону синуса или косинуса: 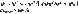Зная уравнение колебаний скорости v(t) всегда можно найти уравнение колебаний ускорения a(t), взяв производную от функции v(t) или вторую производную от функции координаты x(t). Отсюда максимальное ускорение (амплитуда ускорения аmax) равно произведению амплитуды скорости маятника и циклической частоты (или произведению амплитуды координаты маятника и квадрата циклической частоты).	v - скорость колебаний	м/с
ω - циклическая частота колебаний	рад/с
t - время колебаний	с
x - координата, смещение маятника от положения равновесия	м
A - амплитуда колебаний (x max)	м
φ0 - начальная фаза	рад
а - ускорение	м/с2

20.Векторные диаграммы

Графическое представление гармонических колебаний. Векторные диаграммыНаиболее часто употребляются три способа графического представления колебаний.1. Задание графика колебаний х = f(t) в прямоугольной системе координат. По оси абсцисс откладывается время t, а по оси ординат — значение изменяющейся величины х (смещения, скорости, ускорения и др.). Для гармонических колебаний этот график — косинусоида (см. рис. 13.3) или синусоида.

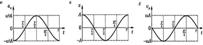
Рис. 13.3

2. Спектральный способ. По оси ординат откладывается амплитуда, а по оси абсцисс — частота гармонических колебаний. Так, например колебательный процес x=5cos4t (м) будет представлен в этом случае вертикальным отрезком прямой длиной 5 м, проведенным от точки с координатой ω = 4 Гц на оси абсцисс (рис. 13.4). Этот способ не дает никакой информации о фазе колебания.

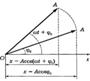Рис. 13.5

Рис. 13.4

3. Способ векторных диаграмм. Пусть величина х изменяется со временем по закону x=Acos(ωt+φ 0 ). На плоскости выбирают произвольно направленную координатную ось Ох. Из начала координат под углом φ 0 , равным начальной фазеколебаний, проводят вектор A ⃗, модуль которого равен амплитуде гармонического колебания A (рис. 13.5). Если вектор A ⃗ вращается

вокруг точки О с постоянной угловой скоростью ω против часовой стрелки, то угол φ между вращающимся вектором и осью Ох в любой момент времени определится выражением φ=(ωt+φ 0 ). Проекция конца вектораA ⃗ будет перемещаться по оси Ох и принимать значения от —А до +А, а колеблющаяся величина будет изменяться со временем по закону x=Acos(ωt+φ 0 ).

Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды A ⃗, отложенного от произвольной точки оси под углом φ 0, равным начальной фазе, и вращающегося с угловой скоростью ω вокруг этой точки.Дифференциальное уравнение гармонических колебаний материальной точки

, или

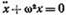, где m — масса точки; k — коэффициент квазиупругой силы (k=тω2). Полная энергия материальной точки, совершающей гармонические колебания,

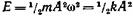
• Период колебаний тела, подвешенного на пружине (пружинный маятник),

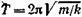
где m — масса тела; k — жесткость пружины. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).

.

21.Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником.

Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:

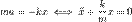
Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:

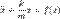, где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.

В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:

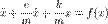
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси,перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Момент инерции относительно оси, проходящей через точку подвеса:

.

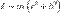Теорема Гюйгенса

Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания/

Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.

Период

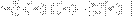
Период малых колебаний физического маятника /Если амплитуда колебаний 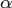мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:

.

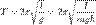22.Бие́ния — явление, возникающее при наложении двух гармонических колебаний, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Биения модулируются по амплитуде. Распространение такого вида колебаний менее эффективно. Частота изменения амплитуды суммарного сигнала равна разности частот двух исходных сигналов.

Биения возникают от того, что один из двух сигналов постоянно отстаёт от другого по фазе и в те моменты, когда колебания происходят синфазно, суммарный сигнал оказывается усилен, а в те моменты, когда два сигнала оказываются в противофазе, они взаимно гасят друг друга. Эти моменты периодически сменяют друг друга по мере того как нарастает отставание.

Биения звука можно слышать при настройке струнн