Закон Ома для неоднородного участка цепи.

Для любой точки внутри проводника напряженность 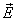результирующего поля равна сумме напряженности поля кулоновских сил и поля сторонних сил . Подставляя в (17.6), получим

Умножим скалярно обе части на вектор , численно равный элементу длины проводника и направленный по касательной к проводнику в ту же сторону, что и вектор плотности тока

Так как скалярное произведение совпадающих по направлению векторов и , равно произведению их модулей, то это равенство можно переписать в виде

С учетом

Интегрируя по длине проводника 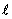от сечения 1 до некоторого сечения 2 и учитывая, что сила тока во всех сечениях проводника одинакова, получаем

Интеграл численно равен работе, совершаемой кулоновскими силами при перенесении единичного положительного заряда с точки 1 в точку 2. В электростатике было показано, что

Таким образом,

где и - значение потенциала в т.1 и т.2.

Интеграл, содержащий вектор напряженности поля, сторонних сил, представляет собой эдс , действующей на участке 1-2

Интеграл

равен сопротивлению участка цепи 1-2.

Подставляя (17.10), (17.9) и (17.8) в (17.7), окончательно получим

Последнее уравнение выражает собой закон Ома в интегральной форме для участка цепи, содержащего эдс и формулируется следующим образом: падение напряжения на участке цепи равно сумме падений электрического потенциала на этом участке и эдс всех источников электрической энергии, включённых на участке.

При замкнутой внешней цепи сумма падений электрических потенциалов и эдс источника равна сумме падений напряжения на внутреннем сопротивлении источника и во всей внешней цепи где или Отсюда

Расчет разветвленных цепей упрощается, если пользоваться правилами Кирхгофа. Первое правило относится к узлам цепи. Узлом называется точка, в которой сходится более чем два тока. Токи, текущие к узлу, считается имеют один знак (плюс или минус), от узла - имеют другой знак (минус или плюс).

Первое правило Кирхгофа является выражением того факта, что в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды и формулируется в следующем виде: алгебраическая сумма токов, сходящихся в узле, равна нулю

Второе правило Кирхгофа является обобщением закона Ома на разветвленные электрические цепи.

Рассмотрим произвольный замкнутый контур в разветвленной цепи (контур 1-2-3-4-1) (рис. 1.2). Зададим обход контура по часовой стрелке и применим к каждому из неразветвленных участков контура закон Ома.

Сложим эти выражения, при этом потенциалы сокращаются и получаем выражение

В любом замкнутом контуре произвольной разветвленной электрической цепи, алгебраическая сумма падений напряжений (произведений сил токов на сопротивление) соответствующих участков этого контура равна алгебраической сумме эдс входящих в контур.

11. Магнитное поле.

Магнитное поле и его характеристики. При прохождении электрического тока по проводнику вокруг него образуется магнитное поле. Магнитное поле представляет собой один из видов материи. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути в направлении, перпендикулярном полю (рис. 34). Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменен и еэлектрического поля приводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля. Электромагнитное поле распространяется со скоростью света, т. е. 300 000 км/с.

Мо многих случаях приходится иметь дело с замкнутыми токами, размеры которых малы по сравнению с расстоянием от них до точки наблюдения. Такие токи будем называть элементарными. Пример подобных токов мы имеем во всех атомах – это движущиеся по замкнутым орбитам электроны. Эти токи, вследствие малости атомных размеров можно считать элементарными.

Рассмотрим плоский круговой виток с током радиуса R (рис.9.1). Характеристиками витка являются: сила тока I, текущего по витку, площадь S, обтекаемая током и ориентация витка в пространстве, определяемая направлением единичного вектора нормали к плоскости витка. Совокупность всех этих трех характеристик образует магнитный момент витка с током, который по определению равен:

В теории магнетизма магнитный момент кругового витка с током играет такую же важную роль, как и электрический дипольный момент в теории электричества.

Принцип суперпозиции

Для магнитного поля, как и для электрического поля, справедлив принцип суперпозиции: поле ,

порождаемое несколькими движущимися зарядами (токами), равно векторной сумме полей ,

порождаемых каждым зарядом (током) в отдельности

т.е., чтобы найти силу, действующую на точку в пространстве, нужно сложить силы, действующие на неё, как показано на рисунке

Магнитное поле кругового тока представляет собой некую восьмёрку с разделением колец в центре кольца, по которому течёт ток. Его схема показана на рисунке

Во многих случаях удобно рассматривать магнитные силовые линии как некоторые упругие растянутые нити, которые стремятся сократиться, а также взаимно отталкиваются друг от друга (имеют взаимный боковой распор). Такое механическое представление о силовых линиях позволяет наглядно объяснить возникновение электромагнитных сил при взаимодействии магнитного поля и Проводника с током, а также двух магнитных полей.

Основными характеристиками магнитного поля являются магнитная индукция, магнитный поток, магнитная проницаемость и напряженность магнитного поля.

12. Закон Ампера.