Расчет напряженности эл. поля с помощью теоремы О-Г.

Электрический заряд.

Свойства электрического заряда. Единица электрического заряда Кулон (Кл). а)Заряд существует в двух видах. Тела, заряженные одноименным знаком отталкиваются, а разноименным притягиваются. б)Электрический заряд инвариантен. Его величина не зависит от системы отсчета, т.е. не зависит от того движется он или покоится. в)Электрический заряд дискретен. Заряд не может уменьшаться до бесконечно малого значения. г)Электрический заряд аддитивен. Заряд системы тел равен сумме зарядов тел входящих в систему. д)подчиняется Закону сохранения электрического заряда: что алгебраическая сумма зарядов любой замкнутой системы остаётся неизменной какие бы процессы не происходили внутри данной системы.

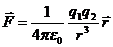Зако́н Куло́на- Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме направлена вдоль прямой, соединяющей заряды, прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними. Закон Кулона в вакууме: .Электрическая постоянная: ε₀=8,85·10^-12 Кл²/Н·м² или Ф/М. В изотропной среде 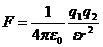. ε=F₀/F – диэлектическая постоянная (проницаемость) среды

Напряжённость эп— векторная физическая величина, опред-я силой действующей на единичный положительный заряд, помещённый в данную точку поля: 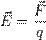[Н/Кл, В/М]

Связь между напряженностью и потенциалом электростатического поля: 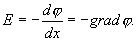Заряд. Закон Кулона.

1) Сила взаимодействия между двумя точечными зарядами: 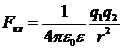[Н]

ε_воздуш = 1, q [Кл] - заряд, r [м] – расстояние между зарядами.

2) Напряженность поля точечного заряда: 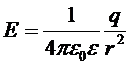, где r – расстояние от заряда до точки, в которой ищем заряд этого поля.

Расчет напряженности эл. поля с помощью теоремы О-Г.

1) Напряженность поля бесконечно заряженной плоскости: 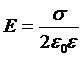где σ – поверхностная плотность заряда на плоскости: 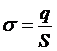[Кл/м²].

2) Напряженность поля двух заряженных плоскостей (поле плоского конденсатора):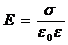

3) Напряженность поля сферы (шара): 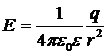, (r ≥ R)

r – расстояние от центра сферы до точки напряженности. Если r < R, то E = 0.

4) Напряженность поля заряженной нити: 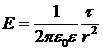, где τ – линейная плотность заряда на нити: 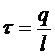[Кл/м].

Метод точечных зарядов.

Примеры применения метода для расчета напряженности и потенциала электростатического поля.

Будем искать, каким образом связаны напряженность электростатического поля, которая является его силовой характеристикой, и потенциал, который есть его энергетическая характеристика поля.
Работа по перемещению единичного точечного положительного электрического заряда из одной точки поля в другую вдоль оси х при условии, что точки расположены достаточно близко друг к другу и x₂—x₁=dx, равна E_xdx. Та же работа равна φ₁—φ₂=dφ. Приравняв обе формулы, запишем
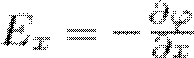(1)
где символ частной производной подчеркивает, что дифференцирование осуществляется только по х. Повторив эти рассуждения для осей у и z, найдем вектор Е:

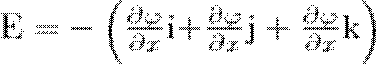
где i, j, k — единичные векторы координатных осей х, у, z.
Из определения градиента следует, что
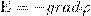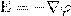или (2)
т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус говорит о том, что вектор напряженности Е поля направлен в сторону уменьшения потенциала.
Для графического представления распределения потенциала электростатического поля, как и в случае поля тяготения, пользуютсяэквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал φ имеет одинаковое значение.
Если поле создается точечным зарядом, то его потенциал, согласно формуле потенциала поля точечного заряда, φ=(1/4πε₀)Q/r .Таким образом, эквипотенциальные поверхности в данном случае — концентрические сферы с цетром в точечном заряде. Заметим также, линии напряженности в случае точечного заряда — радиальные прямые. Значит, линии напряженности в случае точечного зарядаперпендикулярны эквипотенциальным поверхностям.
Линии напряженности всегда перпендикулярны к эквипотенциальным поверхностям. В самом деле, все точки эквипотенциальной поверхности обладают одинаковым потенциалом, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т. е. электростатические силы, которые действуют на заряд, всегда направлены по перпендикурярам к эквипотенциальным поверхностям. Значит, вектор Е всегда перпендикулярен к эквипотенциальным поверхностям, а поэтому линии вектора Е перпендикулярны этим поверхностям.
Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы зарядов можно провести бесконечное множество. Но обычно их проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были равны друг другу. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где гуще расположены эти поверхности, напряженность поля больше.
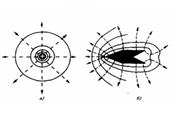
Значит, зная расположение линий напряженности электростатического поля, можно нарисовать эквипотенциальные поверхности и, наоборот, по известному нам расположению эквипотенциальных поверхностей можно найти в каждой точке поля направление и модуль напряженности поля. На рис. 1 в качестве примера показан вид линий напряженности (штриховые линии) и эквипотенциальных поверхностей (сплошные линии) полей положительного точечного электрического заряда (а) и заряженного металлического цилиндра, который имеет на одном конце выступ, а на другом — впадину (б).

Теорема Гаусса.

Поток вектора напряженности. Теорема Гаусса. Применение теоремы Гаусса для расчета электростатических полей.

Поток вектора напряженности.
Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности N_E.

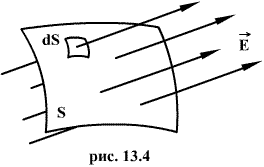Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4).

Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).

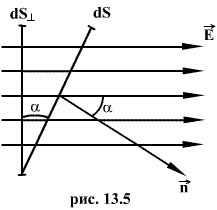
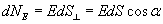
где 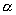- угол между силовой линией и нормалью 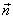к площадке dS; 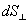- проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен

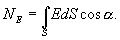(13.4)

Так как 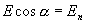, то

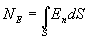(13.5)

где 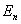- проекция вектора 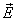на нормаль и к поверхности dS.

Теорема Гаусса.

Поток вектора a через произвольную замкнутую поверхность S равен интегралу дивергенции этого вектора по объему V, ограниченному этой поверхностью:

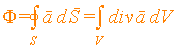(2.15)

Разобъем весь объем, заключенный внутри поверхности S на элементарные кубики типа изображенных на рис. 2.7. Грани всех кубиков можно разделить на внешние, совпадающие с поверхностью S и внутренние, граничащие только со смежными кубиками. Сделаем кубики настолько маленькими, чтобы внешние грани точно воспроизводили форму поверхности. Поток вектора a через поверхность каждого элементарного кубика равен

,

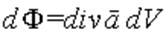а суммарный поток через все кубики, заполняющие объем V, есть

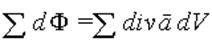(2.16)

Рассмотрим входящую в последнее выражение сумму потоков dФ через каждый из элементарных кубиков. Очевидно, что в эту сумму поток вектора a через каждую из внутренних граней войдет дважды.

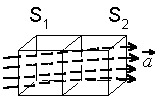Рис. 2.8

Рассмотрим два смежных кубика , поверхности которых обозначены как S1 и S2 (рис. 2.8), причем смежная грань входит как в S1 так и в S2. Очевидно, что при подсчете потока через S1 угол между внешней нормалью к этой грани и вектором а острый и вклад от этой грани в поток будет положительным. А при подсчете потока через S2 вклад от этой грани будет, очевидно, отрицательным.

Тогда полный поток через поверхность S=S₁+S₂будет равен сумме потоков через только внешние грани, поскольку сумма потоков через внутреннюю грань даст ноль. По аналогии можно заключить, что все относящиеся к внутренним граням члены суммы в левой части выражения (2.16), сократятся. Тогда, переходя в силу элементарности размеров кубиков от суммирования к интегрированию, получим выражение (2.15), где интегрирование производится по поверхности, ограничивающей объем.

Заменим в соответствии с теоремой Остроградского-Гаусса поверхностный интеграл в (2.12) объемным

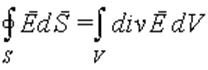и представим суммарный заряд как интеграл от объемной плотности по объему

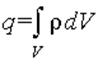
Тогда получим следующее выражение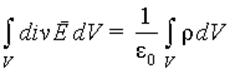

Полученное соотношение должно выполняться для любого произвольно выбранного объема V. Это возможно только в том случае, если значения подинтегральных функций в каждой точке объема одинаковы. Тогда можно записать

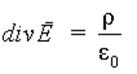(2.17)

Последнее выражение представляет собой теорему Гаусса в дифференциальной форме.

1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость заряжена с постоянной поверхностной плотностью +σ (σ = dQ/dS — заряд, который приходится на единицу поверхности). Линии напряженности перпендикулярны данной плоскости и направлены от нее в каждую из сторон. Возьмем в качестве замкнутой поверхности цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности поля (соsα=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания Е_n совпадает с Е), т. е. равен 2ES. Заряд, который заключен внутри построенной цилиндрической поверхности, равен σS. Согласно теореме Гаусса, 2ES=σS/ε₀, откуда

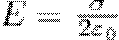(1)

Из формулы (1) следует, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях равна по модулю, иными словами, поле равномерно заряженной плоскости однородно.

2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 2). Пусть плоскости заряжены равномерно разными по знаку зарядами с поверхностными плотностями +σ и –σ. Поле таких плоскостей будем искать как суперпозицию полей, которые создаваются каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательно заряженной плоскости. Слева и справа от плоскостей поля вычитаются (поскольку линии напряженности направлены навстречу друг другу), значит здесь напряженность поля E=0. В области между плоскостями E = E₊ + E_- (E₊ и E_- находятся по формуле (1)), поэтому результирующая напряженность

(2)

Значит, результирующая напряженность поля в области между плоскостями описывается зависимостью (2), а вне объема, который ограничен плоскостями, равна нулю.

3. Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +σ. Т.к. заряд распределен равномернопо поверхности то поле, которое создавается им, обладает сферической симметрией. Значит линии напряженности направлены радиально (рис. 3). Проведем мысленно сферу радиуса r, которая имеет общий центр с заряженной сферой. Если r>R,ro внутрь поверхности попадает весь заряд Q, который создает рассматриваемое поле, и, по теореме Гаусса, 4πr²E = Q/ε₀ , откуда

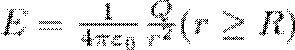(3)

При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. График зависимости Е от r приведен на рис. 4. Если r'<R, то замкнутая поверхность не содержит внутри себя зарядов, значит внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E=0).

4. Поле объемно заряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью ρ (ρ = dQ/dV – заряд, который приходится на единицу объема). Учитывая соображения симметрии, аналогичные п.3, можно доказать, что для напряженности поля вне шара получится тот же результат, что и в случае (3). Внутри же шара напряженность поля будет иная. Сфера радиуса r'<R охватывает заряд Q'=(4/3)πr'³ρ . Поэтому, используя теорему Гаусса, 4πr'²E=Q'/ε₀=(4/3)πr'³ρ/ε₀ . Т.к. ρ=Q/(4/3πR³)) получаем

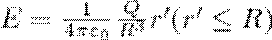(4)

Значит, напряженность поля вне равномерно заряженного шара описывается формулой (3), а внутри его изменяется линейно с расстоянием r' согласно зависимости (4). График зависимости Е от r для рассмотренного случая показан на рис. 5.

5. Поле равномерно заряженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R (рис. 6) равномерно заряжен слинейной плотностью τ (τ = –dQ/dt заряд, который приходится на единицу длины). Из соображений симметрии мы видим, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. Мысленно построим в качестве замкнутой поверхности коаксиальный цилиндр радиуса r и высотой l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы и линии напряженности параллельны), а сквозь боковую поверхность равен 2πrlЕ. Используя теорему Гаусса, при r>R 2πrlЕ = τl/ε₀, откуда

(5)

Если r<R, то замкнутая поверхность внутри зарядов не содержит, поэтому в этой области E=0. Значит, напряженность поля вне равномерно заряженного бесконечного цилиндра задается выражением (5), внутри же его поле равно нулю.

Электрический диполь.

Характеристики электрического диполя. Поле диполя. Диполь в электрическом поле.

Совокупность двух равных по величине разноименных точечных зарядов q, расположенных на некотором расстоянии 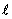друг от друга, малом по сравнению с расстоянием до рассматриваемой точки поля называется электрическим диполем.(рис.13.1)

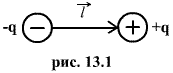
Произведение 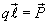называется моментом диполя. Прямая линия, соединяющая заряды называется осью диполя. Обычно момент диполя считается направленным по оси диполя в сторону положительного заряда.

Электроемкость.

Электроемкость уединенного проводника. Конденсатор. Соединения конденсаторов. Энергия системы неподвижных точечных зарядов, заряженного уединенного проводника, заряженного конденсатора, электростатического поля. Пондеромоторные силы.

Энергия системы неподвижных точечных зарядов. Как мы уже знаем, электростатические силы взаимодействия консервативны; значит, система зарядов обладает потенциальной энергией. Будем искать потенциальную энергию системы двух неподвижных точечных зарядов Q₁ и Q₂, которые находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией (используем формулу потенциала уединенного заряда):

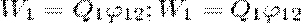
где φ₁₂ и φ₂₁ — соответственно потенциалы, которые создаются зарядом Q₂ в точке нахождения заряда Q₁ и зарядом Q₁ в точке нахождения заряда Q₂. Согласно,

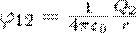и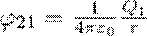

поэтому W₁ =W₂ =W и

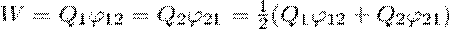
Добавляя к нашей системе из двух зарядов последовательно заряды Q₃, Q₄, ... , можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна

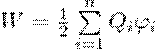(1)
где φ_i — потенциал, который создается в точке, где находится заряд Q_i, всеми зарядами, кроме i-го.
2. Энергия заряженного уединенного проводника. Рассмотрим уединенный проводник, заряд, потенциал и емкость которого соответственно равны Q, φ и С. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, при этом затратив на это работу, которая равна

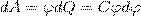");?>" alt="элементарная работа сил электрического поля заряженного проводника">

Чтобы зарядить тело от нулевого потенциала до φ, нужно совершить работу

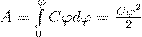(2) Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:

(3)
Формулу (3) можно также получить и условия, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Если φ - потенциал проводника, то из (1) найдем

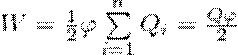где Q=∑Q_i - заряд проводника.

3. Энергия заряженного конденсатора. Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы (3) равна
(4) где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора.
Используя выражение (4), будем искать механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. Для этого сделаем предположение, что расстояние х между пластинами изменилось на величину dx. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fdx = — dW, откуда
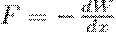(5) Подставив в (4) выражение для емкости плоского конденсатора, получим

(6) Продифференцировав при фиксированном значении энергии (см. (5) и (6)), получим искомую силу:

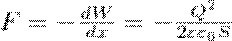где знак минус указывает, что сила F является силой притяжения.
4. Энергия электростатического поля. Используем выражение (4), которое выражает энергию плоского конденсатора посредством зарядов и потенциалов, и спользуя выражением для емкости плоского конденсатора (C=ε₀εS/d) и разности потенциалов между его обкладками (Δφ=Ed. Тогда

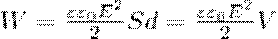где V= Sd — объем конденсатора. Формула (7) говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е.
Объемная плотность энергии электростатического поля (энергия единицы объема)

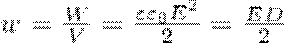Выражение (8) справедливо только для изотропного диэлектрика, для которого выполняется соотношение: Р = æε₀Е.

Формулы (4) и (7) соответственно выражают энергию конденсатора через заряд на его обкладках и через напряженность поля. Возникает вопрос о локализации электростатической энергии и что является ее носителем — заряды или поле? Ответ на этот вопрос может дать только опыт. Электростатика занимается изучением постоянных во времени поля неподвижных зарядов, т. е. в ней поля и попродившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на данный вопрос не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать отдельно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, которые способны переносить энергию. Это убедительно подтверждает основное положение теории близкодействия о том, что энергия локализована в поле и что носителем энергии является поле.

8. Постоянный электрический ток.

Основные характеристики электрического тока. ЭДС и напряжение. Закон Ома для однородного участка цепи в интегральной и дифференциальной формах. Электрическое сопротивление. Проводимость. Соединение проводников. Температурная зависимость сопротивлений.

Электрическим током называют направленное движение заряженных частиц. Количественными характеристиками тока являются его сила тока (отношение заряда: переносимого через поперечное сечение проводника в единицу времени):

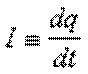
и его плотность, определяемая соотношением:

.

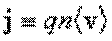Единицей измерения силы тока является ампер (1А - характерное значение тока, потребляемого бытовыми электронагревательными приборами).Необходимыми условиями существования тока являются наличие свободных носителей зарядов, замкнутой цепи и источника ЭДС (батареи), поддерживающего направленное движение.Электрический ток может существовать в различных средах: в металлах, вакууме, газах, в растворах и расплавах электролитов, в плазме, в полупроводниках, в тканях живых организмов.

При протекании тока практически всегда происходит взаимодействие носителей зарядов с окружающей средой, сопровождающееся передачей энергии последней в виде тепла. Роль источника ЭДС как раз и состоит в компенсации тепловых потерь в цепях.

Электродвижущая сила (ЭДС) 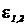, действующей на участке цепи 1-2, называется линейный интеграл

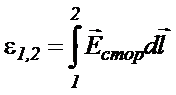
численно равна работе 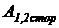, совершаемой сторонними силами при перемещении по проводнику единичного положительного заряда из точки 1 в точку 2. Работа производится за счет энергии источника тока.

Электрический ток в металлах обусловлен движением относительно свободных электронов через кристаллическую решетку. Причины существования свободных электронов в проводящих кристаллах может быть объяснена только на языке квантовой механики.

сила электрического тока, протекающего по проводнику, пропорциональна приложенной к его концам разности потенциалов (закон Ома). Постоянный для выбранного проводника коэффициент пропорциональности между током и напряжением называют электрическим сопротивлением:

(3)

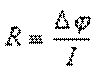
Сопротивление измеряют в омах (сопротивление человеческого тела составляет около 1000 Ом).

Напряжение.

Разность потенциалов.

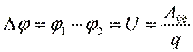
Напряжение.

Разность потенциалов.

Параллельное:

Последовательное:

9. Работа и мощность электрического тока.

Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов 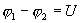, тогда работу по переносу заряда q на этом участке равна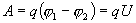

По определению I= q/t. откуда q= I t. Следовательно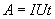

Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил

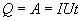(17.13)

Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме.

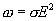(17.14)

Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.

Закон Био-Савара-Лапласа.

Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды. Важнейшая особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды. Опыт показы­вает, что характер воздействия магнитного поля на ток различен в зависимости от формы проводника, по которому течет ток, от расположения проводника и от направления тока. Следовательно, чтобы охарактеризовать магнитное поле, надо рассмотреть его действие на определенный ток. Закон Био — Савара — Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде 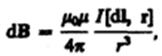где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r—радиус-вектор, проведанный из элемента dlпроводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.

Модуль вектора dB определяется выражением 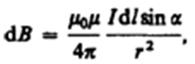(110.2)где a — угол между векторами dl и r.

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности: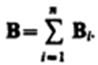

Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную сим­метрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.

1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что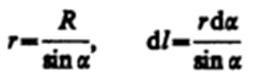

(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна

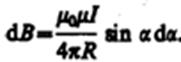(110.4)

Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),

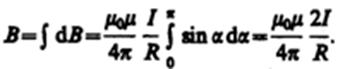
Следовательно, магнитная индукция поля прямого тока

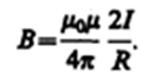(110.5)

2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

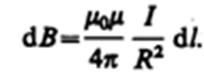
Тогда

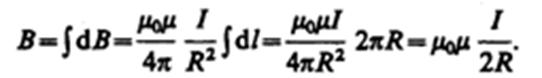
Следовательно, магнитная индукция поля в центре кругового проводника с током

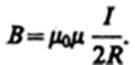
Электромагнитная индукция.

МАГНИТНАЯ ИНДУКЦИЯ

-векторная физическая величина, характеризующая магнитное поле.

Вектор магнитной индукции всегда направлен по касательной к магнитной линии

Расчетная формула:

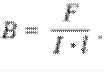
где F- сила, действующая со стороны магнитного поля на проводник с током ( H );
I - сила тока в проводнике ( A );
l - длина проводника ( м ).
Единица измерения индукции магнитного поля в СИ:
[ B ] = 1Тл ( тесла).

МАГНИТНЫЙ ПОТОК

Контур, помещенный в однородное магнитное поле, пронизывается магнитным потоком
( потоком векторов магнитной индукции).

Ф - магнитный поток, пронизывающий площадь контура, зависит от
величины вектора магнитной индукции, площади контура и его ориентации относительно линий индукции магнитного поля.

Если вектор магнитной индукции перпендикулярен площади контура, то магнитный поток максимальный.

Если вектор магнитной индукции параллелен площади контура, то магнитный потокравен нулю.

Замкнутый контур

Направление индукционного тока в замкнутом контуре определяется по правилу Ленца.

Правило Ленца

Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует изменению магнитного потока, которым он вызван.

Применение правила Ленца
1. показать направление вектора В внешнего магнитного поля;
2. определить увеличивается или уменьшается магнитный поток через контур;
3. показать направление вектора Вi магнитного поля индукционного тока ( при уменьшении магнитного потока вектора В внешнего м.поля и Вi магнитного поля индукционного тока должны быть направлены одинаково, а при увеличениии магнитного потока В и Вi должны быть направлены противоположно );
4. по правилу буравчика определить направление индукционного тока в контуре.

Энергия магнитного поля.

Электромагнитные колебания.

Колебательным контуром называется электрическая цепь, состоящая из последовательно соединенных конденсатора с емкостью C и катушки с индуктивностью L.

Если зарядить конденсатор колебательного контура некоторым зарядом q, то он приобретет энергию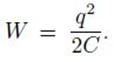

В контуре возникают электромагнитные колебания, и энергия заряженного конденсатора переходит в энергию магнитного поля катушки

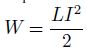и наоборот.

Для свободных незатухающих колебаний в контуре циклическая частота определяется формулой: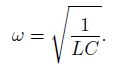

Период свободных колебаний в контуре определяется формулой Томсона: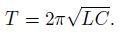

Если в LC-контур последовательно с L, C и R включить источник переменного напряжения, то в цепи возникнут вынужденные электрические колебания. Такие колебания принято называть переменным электрическим током.

В цепь переменного тока можно включать три вида нагрузки — конденсатор, резистор и катушку индуктивности.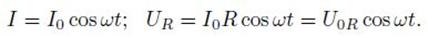

Конденсатор оказывает переменному току сопротивление, которое можно посчитать по формуле: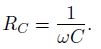

Ток, текущий через конденсатор, по фазе опережает напряжение на π/2 или на четверть периода, а напряжение отстает от тока на такой же фазовый угол.

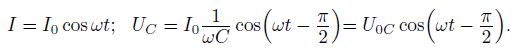
Катушка индуктивности оказывает переменному току сопротивление, которое можно посчитать по формуле: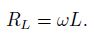

Ток, текущий через катушку индуктивности, по фазе отстает от напряжения на π/2 или на четверть периода. Напряжение опережает ток на такой же фазовый угол.

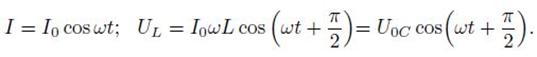
Классификация магнетиков.

В то время как диэлектрическая проницаемость ε у всех веществ всегда больше единицы (диэлектрическая восприимчивость κ>0), магнитная проницаемость μ может быть как больше единицы, так и меньше единицы (соответственно магнитная восприимчивость χ >0 и χ<0). Поэтому магнитные свойства веществ отличаются гораздо большим разнообразием, чем электрические свойства.

Диамагнетики – вещества, характеризуемые отрицательным значением магнитной восприимчивости χ. Вследствие этого вектор намагничивания 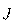в этих веществах направлен противоположно внешнему намагничивающему полю 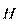. Диамагнетиками являются, например, вода (χ = - 9∙10^-6), серебро (χ = - 2,6∙10^-5), висмут (χ = - 1,7∙10^-4).

Парамагнетики – характеризуются положительным значение χ , ведут они себя подобно диэлектрикам с диэлектрической проницаемостьюε>1, то есть вектор 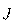в этих веществах параллелен намагничивающему полю 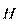. К парамагнетикам относятся алюминий (χ = 2,1∙10^-6), платина (χ = 3∙10^-4), хлористое железо (χ = 2,5∙10^-3).

Ферромагнетики – особый вид магнетиков, отличающийся от других магнетиков следующими характерными признаками: 1) высоким значением магнитной восприимчивости; 2) зависимостью магнитной проницаемости μ от напряженности магнитного поля, вследствие чегозависимость 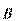от